Lesson 13
Multiples of 100
Warm-up: Estimation Exploration: Marching Band (10 minutes)
Narrative
The purpose of an Estimation Exploration is to practice the skill of estimating a reasonable answer based on experience and known information. It gives students a low-stakes opportunity to share a mathematical claim and the thinking behind it (MP3). Asking yourself “Does this make sense?” is a component of making sense of problems (MP1), and making an estimate or a range of reasonable answers with incomplete information is a part of modeling with mathematics (MP4).
Launch
- Groups of 2
- Display the image.
- “What is an estimate that’s too high? Too low? About right?”
- 1 minute: quiet think time
Activity
- “Discuss your thinking with your partner.”
- 1 minute: partner discussion
- Record responses.
- “Which groups on the field did you count as part of the marching band?” (I counted only the performers in the band uniforms. I included everyone on the field.)
Student Facing
How many people are in the marching band?
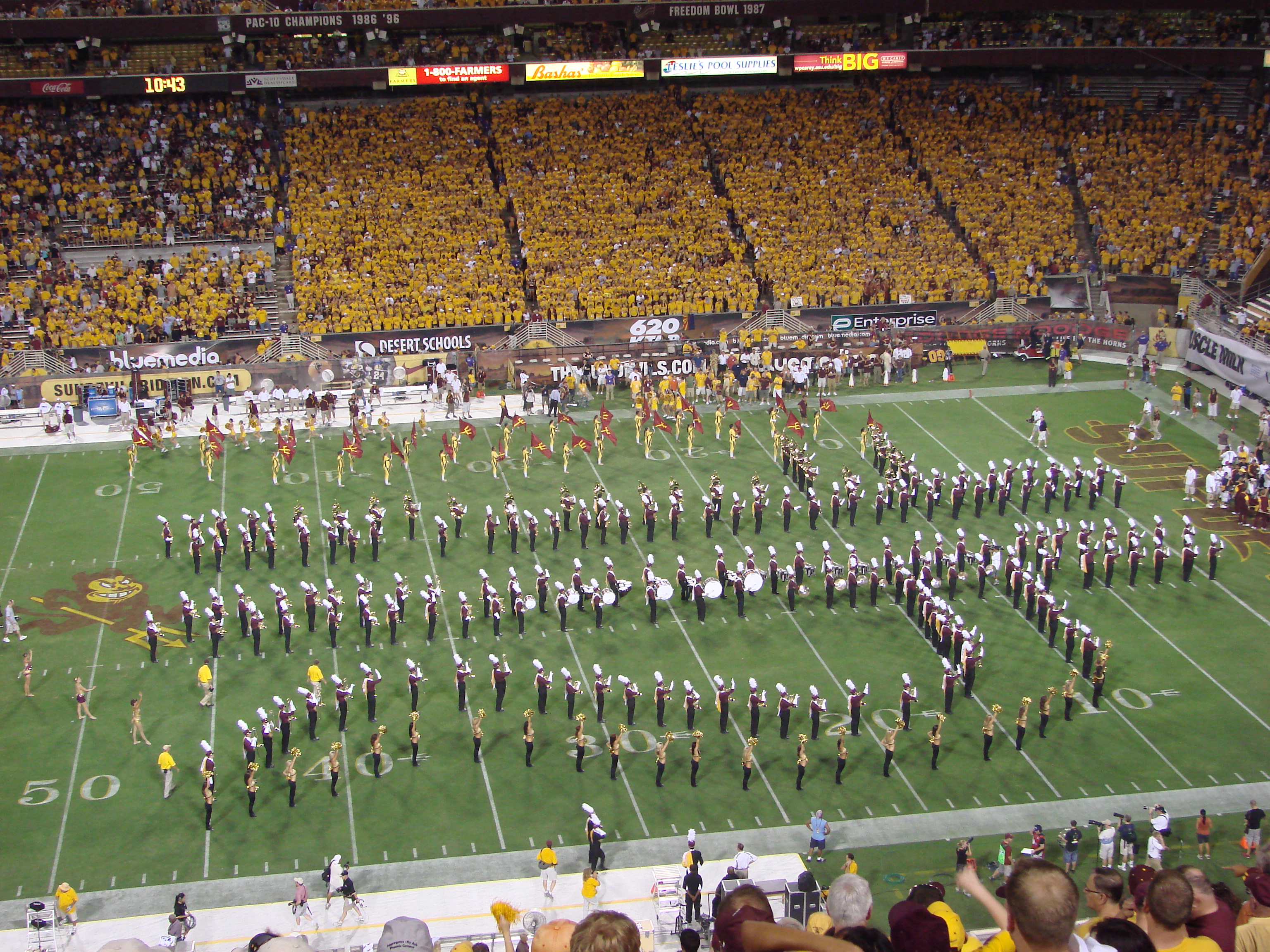
Record an estimate that is:
| too low | about right | too high |
|---|---|---|
| \(\phantom{\hspace{2.5cm} \\ \hspace{2.5cm}}\) | \(\phantom{\hspace{2.5cm} \\ \hspace{2.5cm}}\) | \(\phantom{\hspace{2.5cm} \\ \hspace{2.5cm}}\) |
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “Notice that many of our estimates are expressed in terms of tens and hundreds. Why might that be? Why don’t we estimate that there are about, say, 163 people or 248 people in the picture?” (If we are estimating, we aren’t trying to guess the exact number. Tens and hundreds are easy to think about.)
- “It is often helpful to get a sense of a quantity (how many, how much, how long, etc.) with groups of 10 or groups of 100. Numbers like 50 and 90 that are groups of 10 can be called ‘multiples of 10.’ Numbers like 200 or 700 that are groups of 100 can be called ‘multiples of 100.’”
- “When we estimate, we often name the multiple of 10 or 100 that we think the number is close to.”
- “But how do we decide whether a number is close to some multiple of 10 or 100? We’ll think more about this question in the next activity.”
Activity 1: About 100? Close to 100? (10 minutes)
Narrative
The purpose of this activity is for students to think about what it means for numbers to be close to multiples of 100. There is no definition given about what “close to” means during the activity, so students may interpret the term in different ways.
Supports accessibility for: Memory
Launch
- Groups of 2
- Display the first problem.
- “Take a minute to look at the numbers of people in different parts of a school during a school day. What do you notice? What do you wonder?” (There aren’t many people in the library. There are a lot of people in the school. Are there any other places where people could be in the school?)
- 1 minute: quiet think time
- Share and record responses.
Activity
- “For each room, decide if there are about 100 people in the room or not. Record the numbers in the table. Be prepared to explain how you decide a number is or is not about 100.”
- 2 minutes: independent work time
- Share responses.
- “Now, work with your partner to decide if the number of people in each part of the school is close to 0, close to 100, or close to 200. If you don’t think a number belongs in any column, set it aside. Be prepared to explain your reasoning.”
- 2–3 minutes: partner work time
- Monitor for students who provide reasoning for where they would place 36, 52, and 163. Ask them to share during the synthesis.
Student Facing
-
Here are the numbers of people in different parts of a school at noon during a school day.
- playground: 94
- cafeteria: 163
- art room: 36
- library: 13
- classrooms: 216
- gymnasium: 109
- music room: 52
Where in the school would you say that there are about 100 people?
Record the numbers in the table. Be prepared to explain your reasoning.
about 100 not about 100 \(\phantom{\hspace{2.5cm} \\ \hspace{2.5cm}}\) \(\phantom{\hspace{2.5cm} \\ \hspace{2.5cm}}\) -
Now decide if the number of people in each part of the school is close to 0, close to 100, or close to 200.
If you don’t think a number belongs in any column, set it aside. Be prepared to explain your reasoning.
close to 0 close to 100 close to 200 \(\phantom{\hspace{2.2cm} \\ \hspace{2.2cm}}\) \(\phantom{\hspace{2.2cm} \\ \hspace{2.2cm}}\) \(\phantom{\hspace{2.2cm} \\ \hspace{2.2cm}}\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “How did you decide whether a number is close to 0, 100, or 200?” (I thought about whether it was almost that number, like 94 is almost 100. I decided between the choices that were there—like for 216, it was closer to 200 than to 0 or 100.)
- “How did you decide if a number doesn’t belong to any of these groups?” (If a number seemed far away from all the choices, then I set it aside. Like 52 wasn’t close to 0 or 100 because it’s almost right in the middle.)
- “What if the table showed ‘closer to 0,’ ‘closer to 100,’ and ‘closer to 200?’ Would it change where each number goes? Would you be able to place all the numbers in the table?” (Yes, because I would just be choosing the number that’s closer than the other numbers, not saying it’s really close to the number.)
Activity 2: Close to Multiples of 100 (25 minutes)
Narrative
The purpose of this activity is for students to locate two- and three-digit numbers on a series of number lines. The endpoints of each number line are multiples of 100, and the space between them is partitioned into ten equal intervals. As they locate the numbers, students recognize each tick mark as a multiple of 10. Later in the activity, students use a number line to name the closest multiple of 100 to a given number. When students choose the correct number line and accurately place each number on the number line they attend to precision and show an understanding of place value (MP6, MP7).
Advances: Speaking, Representing
Launch
- Groups of 4
- “What do you know about the number line?” (Each point on the number line can represent a number. You can add or subtract by moving right or left on the number line. It can show distance between numbers, like the number 10 is 10 away from 0.)
- 1 minute: quiet think time
- Share and record responses.
- “Take a look at the number lines in the first problem. What do you notice about them? What do you wonder?” (Students may notice: Each number line has two multiples of 100. There are tick marks between the numbers. Students may wonder: Why don’t the number lines go higher or lower? What numbers do the tick marks represent?)
- 30 seconds: quiet think time
- Share responses.
- Display the number line:
- “Do you see multiples of 100 in this number line?” (Yes, 100 and 200)
- “What numbers do you think the unlabeled tick marks represent?” (Tens, groups of 10, numbers that we get if we count up by 10 starting from 100, multiples of 10) “Let’s name them!” (100, 110, . . . , 200)
- Label the first few tick marks.
- “Can you estimate where 113 goes on the number line?” (Between the second and third tick marks, but closer to the second tick mark. Or between 110 and 120, but closer to 110.)
- Assign one set of numbers (A, B, C, D, or E) to each group of 4.
Activity
- “Work with your group to decide on which number line each number should go. Locate each number on the number line with a dot, and label it. Then, complete the second problem.”
- 5–7 minutes: small group work time
- After students place 364 on a number line, pause for a discussion. Ask each group to share one of their numbers and how they knew on which number line to place it.
- “On which number line did you place 364?” (The number line with 300 and 400.)
- “How did you decide which multiple of 100 was the closest?” (Once I located 364 on my number line I could tell it was closer to 400. I counted the tick marks back to 300 and up to 400 and it was less tick marks to get to 400, so it was closer.)
- “Complete the last problem on your own.”
- 2–3 minutes: independent work time
Student Facing
Your teacher will assign a set of numbers to you.
| A | 94 | 36 | 109 | 163 | 229 |
|---|---|---|---|---|---|
| B | 24 | 52 | 216 | 11 | 481 |
| C | 187 | 135 | 67 | 83 | 241 |
| D | 332 | 154 | 408 | 296 | 45 |
| E | 279 | 205 | 377 | 449 | 73 |
-
Work with your group to decide on which number line each number should go. Then, locate and label each number on the number line.
-
Locate and label 364 on the correct number line.
- Name two multiples of 100 that are closest to 364.
- Of the two multiples of 100 you named, which one is 364 closer to?
- Write the numbers assigned to you earlier. For each number, name the nearest multiple of 100.
number nearest multiple of 100
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
If students place a number on a number line on which it doesn’t belong, such as placing 216 on the number line that goes from 100 to 200, consider asking:
- “Tell me how you decided to place 216 on that number line?”
- “Can you show me where 216 would be on that number line?”
Activity Synthesis
- “How can you tell which multiple of 100 a number is closest to?” (The endpoints of the number lines are multiples of 100. From the number line, we can tell whether a point is closer to one end or the other. We can tell if a point is in the lower half or upper half of the number line. We can count the tick marks to each multiple of 100 to decide which one is closer.)
Lesson Synthesis
Lesson Synthesis
“Today we located and labeled numbers on number lines, and decided which multiple of 100 a given number would be closest to.”
“Look back at the table from the last activity. What do you notice about the nearest multiples of 100 for your set of numbers?” (Sometimes the nearest multiple is greater than the numbers, sometimes it is less. Sometimes the nearest multiple of 100 is 0. Some multiples of 100 are really far away from the original number. For example, 449 is 49 away from 400. Two numbers that are very different or seem far apart could have the same nearest multiple of 100. For example, 67 and 135 both have 100 as their nearest multiple of 100.)
Cool-down: Locate, Label, and Name (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.




