Lesson 10
Measure with a Torn Tape
Warm-up: True or False: Constant Difference (10 minutes)
Narrative
Launch
- Display one statement.
- “Give me a signal when you know whether the statement is true and can explain how you know.”
- 1 minute: quiet think time
Activity
- Share and record answers and strategy.
- Repeat with each statement.
Student Facing
Decide if each statement is true or false. Be prepared to explain your reasoning.
- \(10 - 0 = 12 - 2\)
- \(8 - 4 = 10 - 6\)
- \(12 - 4 = 10 - 3\)
- \(15 - 2 = 13 - 0\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “How could we change the third equation to make it true?” (We could change the 3 to a 2 because the 12 went down by 2 and 4 also went down by 2. The difference would stay the same.)
Activity 1: The Notebook Problem (15 minutes)
Narrative
The purpose of this activity is for students to apply conservation of length by measuring with a tool that does not start at zero. Until now, students have focused on measuring by lining up the edge of an object with zero. In this activity, students consider how the units on a ruler, and in later lessons, a number line, can help us solve problems and measure even when we are not starting at zero. It is important for students to recognize that the tick marks show a consistent distance between numbers, so any part of the ruler can show a specific number of units. The synthesis focuses on how addition (counting on from the starting number) and subtraction can be used to find the length of an object. The teacher records students’ thinking with an equation with a question mark for the unknown.
It is recommended that students use rulers to measure the length of smaller objects (2–10 inches) in this activity. This smaller number range helps students connect what they notice about measuring starting at different numbers on the ruler to familiar addition and subtraction equations within 20. However, this activity can be adapted to use measuring tapes or yardsticks to measure longer objects if they are available.
When students measure objects starting at different non-zero spots on the ruler and observe what stays the same (the difference) and what changes (the starting and ending spots) they observe a structure which repeats itself no matter which spot they on the ruler they begin the measurement (MP7, MP8).
Supports accessibility for: Conceptual Processing, Visual-Spatial Processing
Required Materials
Materials to Gather
Required Preparation
- Each group of 2 needs access to several objects between 2–10 inches long. Consider using classroom objects such as markers, colored pencils, paperclips, or other objects or images used in previous activities.
Launch
- Groups of 2
- Give each student a ruler.
- Display the image.
Activity
- “Han measured the same notebook as Jada. Jada’s measuring tape was torn, but she got the same answer. How did that happen?”
- 1 minute: quiet think time
- “Work with a partner to figure out how Jada got the same answer as Han. Be prepared to explain your thinking.”
- 3–4 minutes: partner discussion
- Monitor for a student who explains the problem as \(10 - 2 = {?}\) and one who explains the problem as \(2 + {?} = 10\).
- Share responses.
- “Now, using your ruler, you and your partner should find 1 thing in the classroom to measure without starting at zero. Each of you should start at a different number and compare your measurements.”
- “Don’t forget to include the unit with your measurement and to use a question mark for the unknown in your equation.”
- 5 minutes: partner work time
- Monitor for students who discuss:
- that the length must be the same because the object doesn’t change
- the equations they write have the same value or show the same relationship
- the relationship between the numbers in their different expressions (for example, “the numbers I subtracted are two more than yours because I moved the object 2 inches over on the ruler. The difference is the same.”)
Student Facing
Jada and Han used an inch ruler to measure the short side of a notebook.
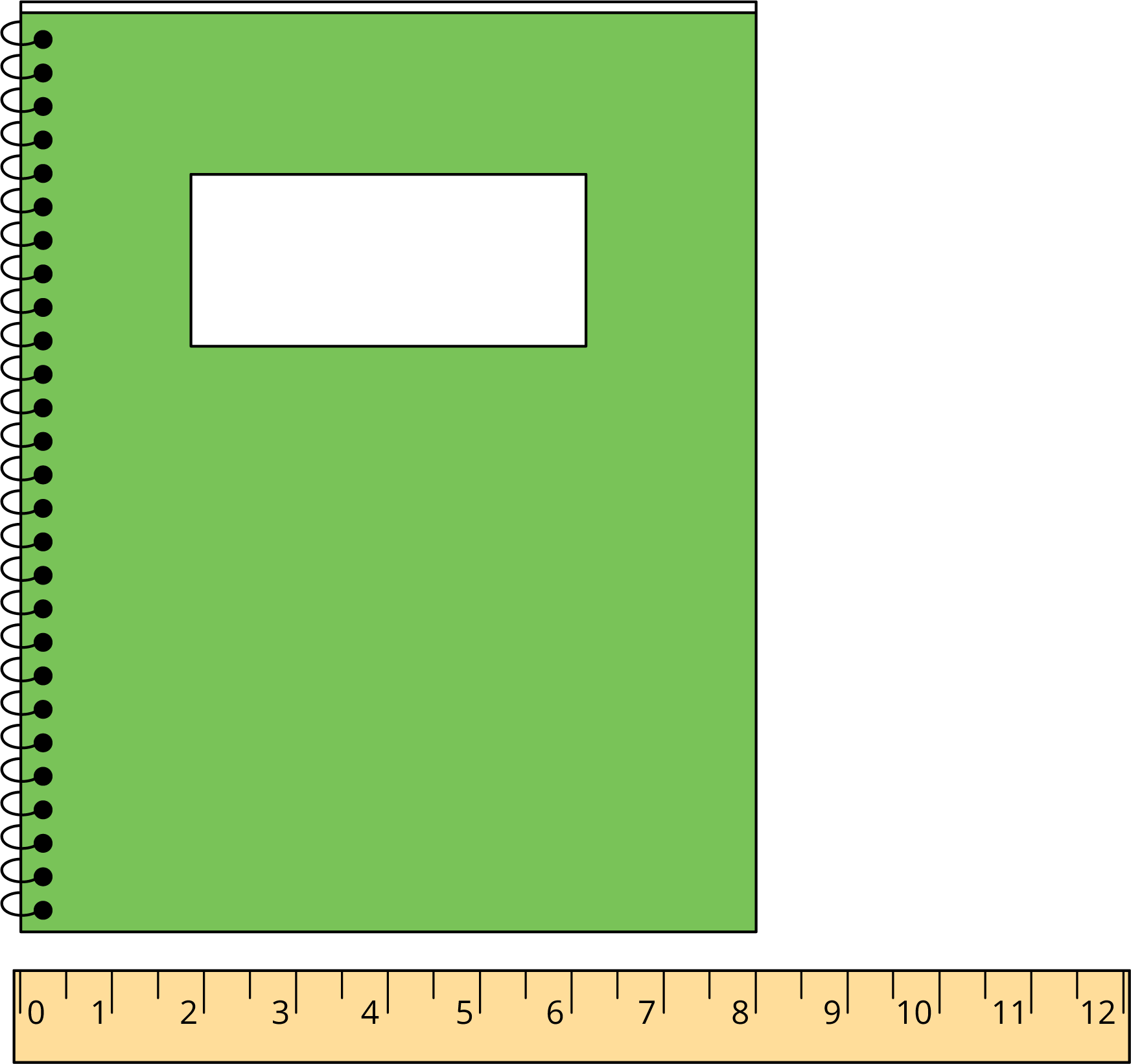
Han says 8 inches.

Jada says 8 inches.
- How did Han and Jada get the same measurement?
- Write an equation that could show Jada’s thinking.
-
Measure an object using Jada’s method.
- I measured a ________________________________.
- I started with the number ____________.
- I ended with the number ____________.
- Equation: ________________________________.
- The length of my object is ____________.
- What do you notice about you and your partner’s measurements?
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
Students may find the correct length when counting length units on the measuring tool, but identify the length as the total number if they represent their measurement with an addition equation. (For example, they count on from 2 inches to 10 inches on the ruler and write \(2 + 8 = 10\), but say the length of the object is 10). Consider asking:
- “How did you measure the ___?”
- “What do the numbers in your equation represent?”
Activity Synthesis
- Invite selected students to share their measurements and their reasoning.
- Write equations that correspond to the students’ thinking using a question mark to represent the unknown value.
- “Why do you think you get the same measurement each time, even if you measure starting from a different place?” (The object didn't change, so the length has to stay the same. The total length in inches is still the same between the number that you start with and end with.)
Activity 2: A Desktop to Measure (20 minutes)
Narrative
In this activity, students apply the methods they used in Activity 1 to solve a similar problem independently. They write equations to represent each problem. Students may write an equation with an unknown to represent the problem or a complete equation after they have solved. Students make connections to addition and subtraction as they count on or subtract to determine the length of objects when measuring with a torn tape measure. In the activity synthesis, students compare 2 different equations that could represent the problem.
Advances: Conversing, Reading
Launch
- Groups of 2
Activity
- “Now that you have had some practice measuring without starting at zero, you will work on your own to help Lin solve her problem.”
- “Lin was trying to measure her desktop. Her measuring tape was tangled and she couldn’t start from the beginning of the tape. She decided to start measuring at 16 in.”
- “How long is each side of the desktop?”
- 8 minutes: independent work time
- “Now take a few minutes to discuss your solutions for Lin with your partner.”
- 2 minutes: partner discussion
- Monitor for students who write an addition and subtraction equation with a question mark for the unknown for the length of the short side of the desktop.
Student Facing
Lin is measuring her desktop in inches.
-
What is the length of the long side of the desktop? Show your thinking using drawings, numbers, or words.

Equation: ________________________________
The long side of the desktop is ______________.
-
What is the length of the short side of the desktop? Show your thinking using drawings, numbers, or words.

Equation: ________________________________
The short side of the desktop is ____________.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Invite previously selected students share the equations they used to find the length of the short side of the desk or display:
- \(34 - 16 = {?}\)
- \(16 + {?} = 34\)
- “Do both of these equations represent how Lin could find the length of the short side of her desk? How do you know?”
Lesson Synthesis
Lesson Synthesis
“Today, you learned that you can measure the length of objects using a measuring tool without starting at 0. We saw that you can always count the number of length units from one end of an object to the other. We also agreed that you could use addition or subtraction to find the difference when measuring by using the numbers on both ends of the length you measure.”
“What was your preferred method? Why?”
Cool-down: Torn Tape (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.