Lesson 17
Drawing Triangles
Problem 1
Use a protractor to try to draw each triangle. Which of these three triangles is impossible to draw?
- A triangle where one angle measures \(20^\circ\) and another angle measures \(45^\circ\)
- A triangle where one angle measures \(120^\circ\) and another angle measures \(50^\circ\)
-
A triangle where one angle measures \(90^\circ\) and another angle measures \(100^\circ\)
Solution
For access, consult one of our IM Certified Partners.
Problem 2
A triangle has an angle measuring \(90^\circ\), an angle measuring \(20^\circ\), and a side that is 6 units long. The 6-unit side is in between the \(90^\circ\) and \(20^\circ\) angles.
- Sketch this triangle and label your sketch with the given measures.
- How many unique triangles can you draw like this?
Solution
For access, consult one of our IM Certified Partners.
Problem 3
A triangle has sides of length 7 cm, 4 cm, and 5 cm. How many unique triangles can be drawn that fit that description? Explain or show your reasoning.
Solution
For access, consult one of our IM Certified Partners.
Problem 4
A triangle has one side that is 5 units long and an adjacent angle that measures \(25^\circ\). The two other angles in the triangle measure \(90^\circ\) and \(65^\circ\). Complete the two diagrams to create two different triangles with these measurements.
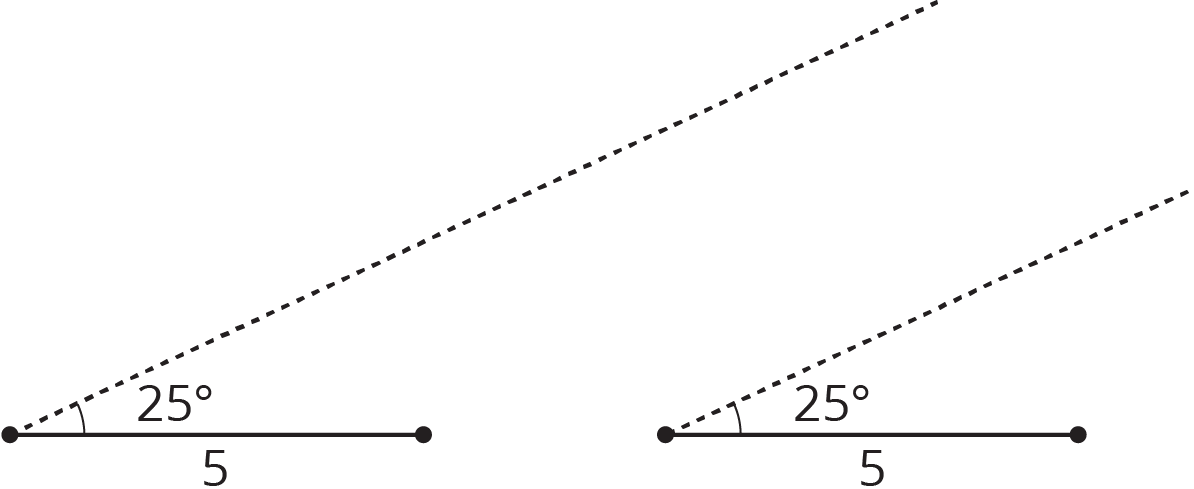
Solution
For access, consult one of our IM Certified Partners.
Problem 5
Is it possible to make a triangle that has angles measuring 90 degrees, 30 degrees, and 100 degrees? If so, draw an example. If not, explain your reasoning.
Solution
For access, consult one of our IM Certified Partners.