Lesson 17

Drawing Triangles

Let’s see how many different triangles we can draw with certain measurements.

17.1: Using a Compass to Estimate Length

  1. Draw a \(40^\circ\) angle.
  2. Use a compass to make sure both sides of your angle have a length of 5 centimeters.

  3. If you connect the ends of the sides you drew to make a triangle, is the third side longer or shorter than 5 centimeters? How can you use a compass to explain your answer?

17.2: How Many Can You Draw?

  1. Draw as many different triangles as you can with each of these sets of measurements:

    1. Two angles measure \(60^\circ\), and one side measures 4 cm.
    2. Two angles measure \(90^\circ\), and one side measures 4 cm.
    3. One angle measures \(60^\circ\), one angle measures \(90^\circ\), and one side measures 4 cm.

  2. Which sets of measurements determine one unique triangle? Explain or show your reasoning.

 


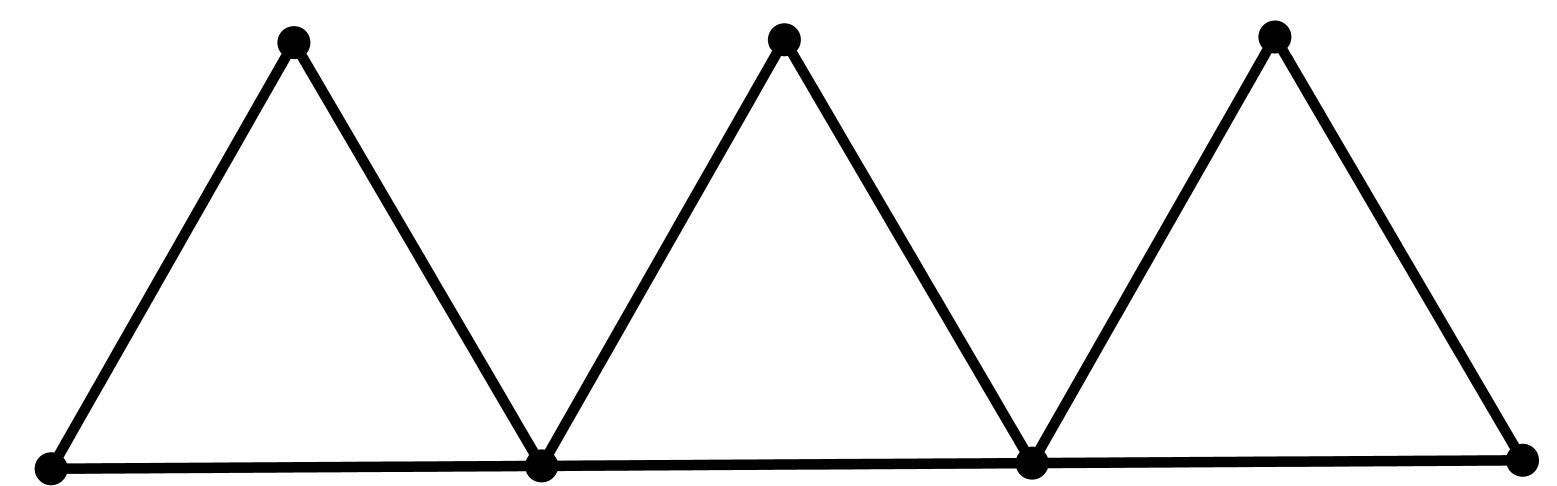
Nine toothpicks are arranged to make 3 equilateral triangles, their bases form a horizontal line.

In the diagram, 9 toothpicks are used to make three equilateral triangles. Figure out a way to move only 3 of the toothpicks so that the diagram has exactly 5 equilateral triangles.

17.3: Revisiting How Many Can You Draw?

Use an applet to draw triangles. Sides can overlap.

  1. Draw as many different triangles as you can with this set of measurements.

     
    1. One angle measures \(40^\circ\), one side measures 4 cm, and one side measures 5 cm.
    2. Do these measurements determine one unique triangle? How do you know?
  2. Draw as many different triangles as you can with each of these sets of angle measurements. Do either of these sets of measurements determine one unique triangle? Explain how do you know.

     
    1. One angle measures \(50^\circ\), one measures \(60^\circ\), and one measures \(70^\circ\).
    2. One angle measures \(50^\circ\), one measures \(60^\circ\), and one measures \(100^\circ\).


Using only the point, segment, and compass tools provided, create an equilateral triangle. You are only successful if the triangle remains equilateral while dragging its vertices around. 

GeoGebra Applet DsB2VFYv

Summary

A triangle has six measures: three side lengths and three angle measures.

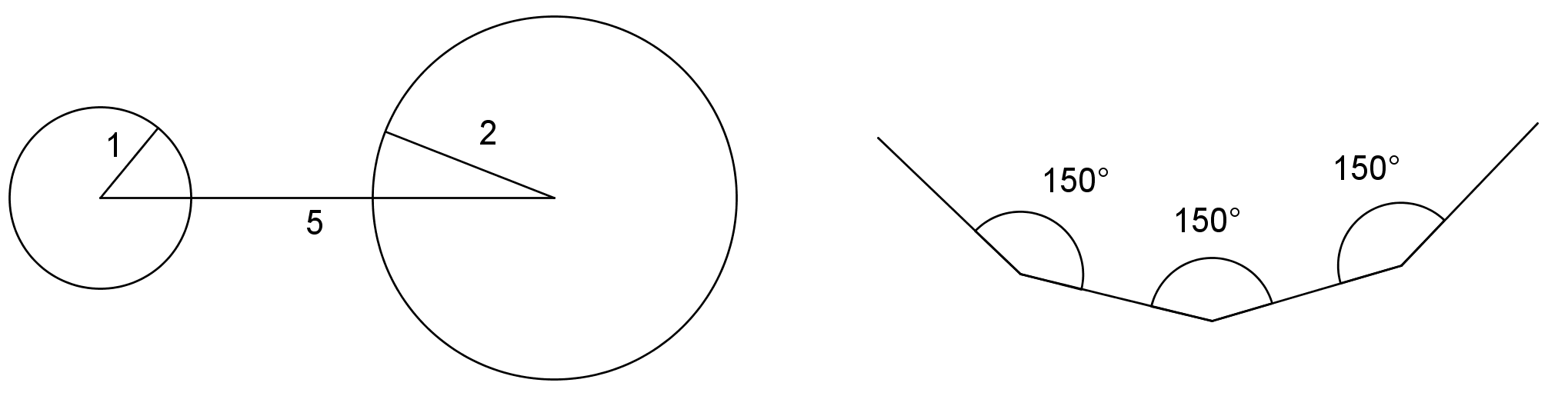
If we are given three measures, then sometimes, there is no triangle that can be made. For example, there is no triangle with side lengths 1, 2, 5, and there is no triangle with all three angles measuring \(150^\circ\).

Two images. First, a segment 5 units, a circle radius 1 unit centered at an endpoint, a circle radius 2 centered at the other endpoint. Second, 4 segments, joined end to end, each angle 150 degrees.

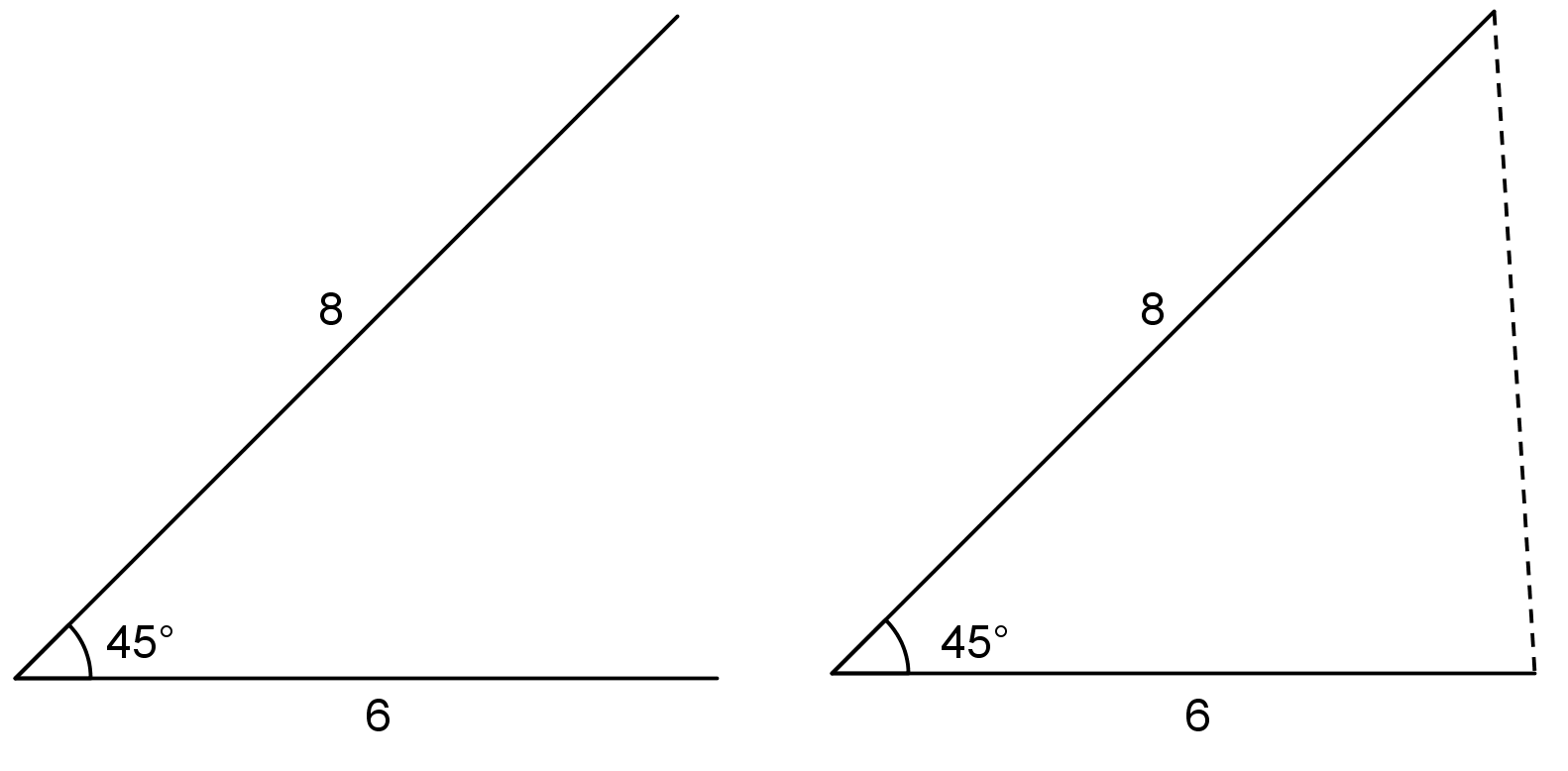
Sometimes, only one triangle can be made. By this we mean that any triangle we make will be the same, having the same six measures. For example, if a triangle can be made with three given side lengths, then the corresponding angles will have the same measures. Another example is shown here: an angle measuring \(45^\circ\) between two side lengths of 6 and 8 units. With this information, one unique triangle can be made.

Two angles.  First, segments length 6 and 8 meet at a 45 degree angle.  Second, segments length 6 and 8 meet at a 45 degree angle, a dotted line connects the other endpoints.

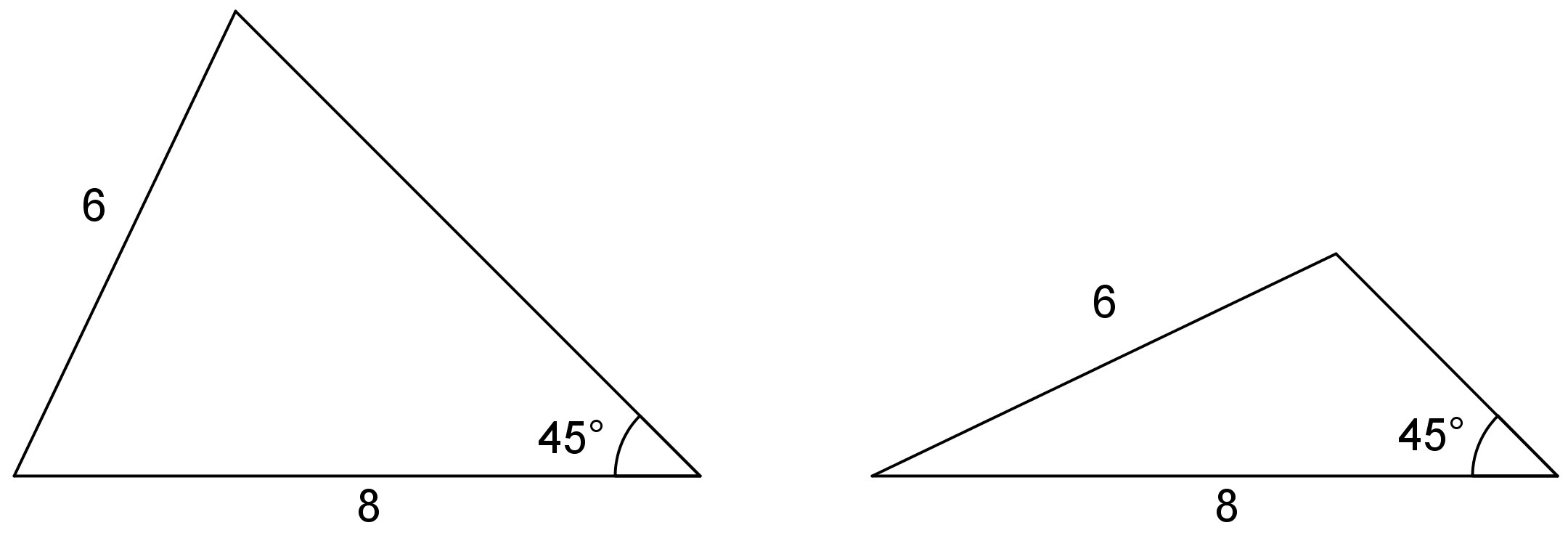
Sometimes, two or more different triangles can be made with three given measures. For example, here are two different triangles that can be made with an angle measuring \(45^\circ\) and side lengths 6 and 8. Notice the angle is not between the given sides.

Two different triangles are shown.  Both triangles have sides with length 6 and 8, both triangles have 45 degree angles, but one triangle is bigger than the other.

Three pieces of information about a triangle’s side lengths and angle measures may determine no triangles, one unique triangle, or more than one triangle. It depends on the information.