Lesson 14

Parallel Lines and the Angles in a Triangle

View Student Lesson

Problem 1

For each triangle, find the measure of the missing angle.

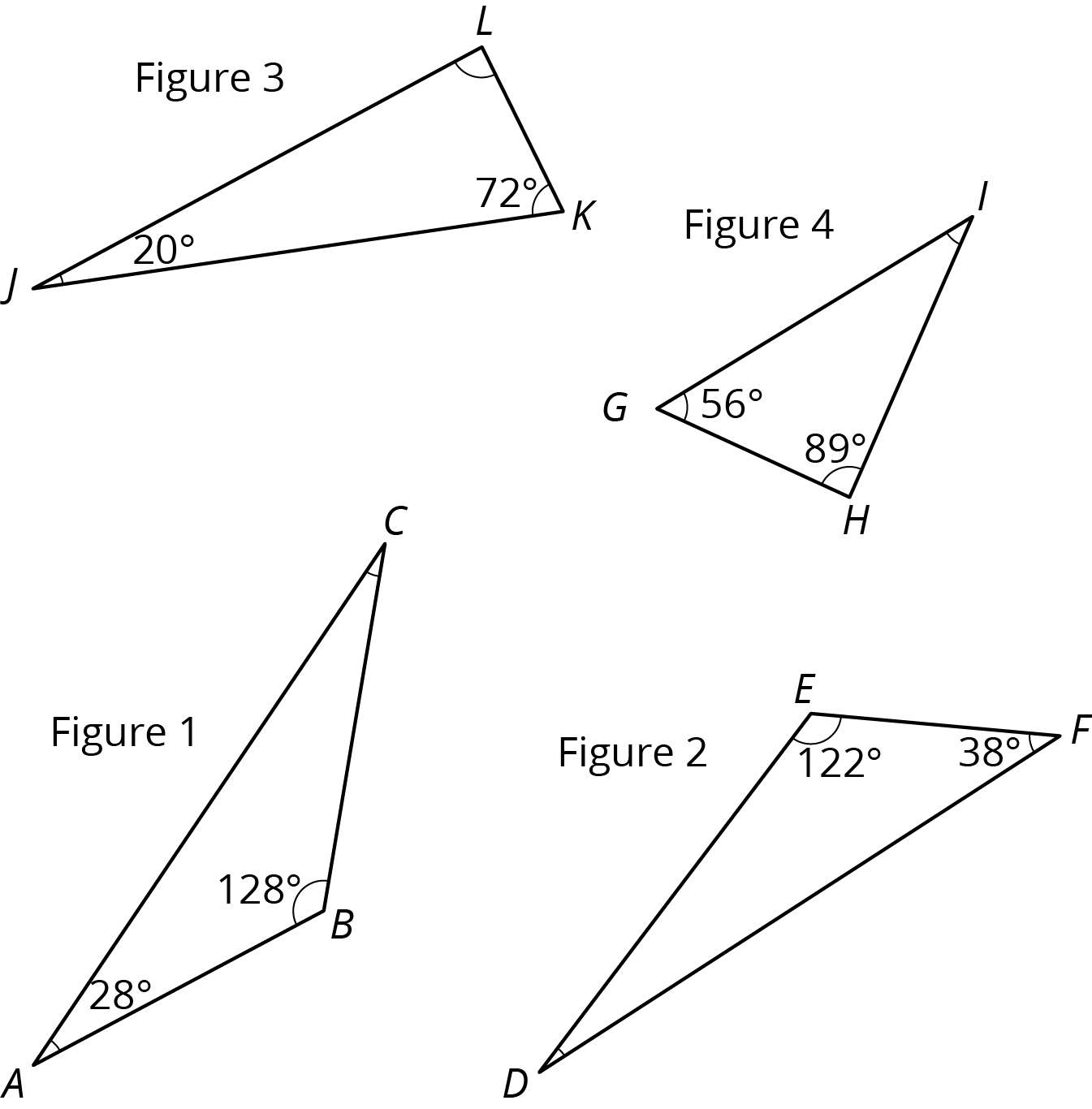
Four triangles. 

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Is there a triangle with two right angles? Explain your reasoning.

Solution

For access, consult one of our IM Certified Partners.

Problem 3

In this diagram, lines \(AB\) and \(CD\) are parallel.

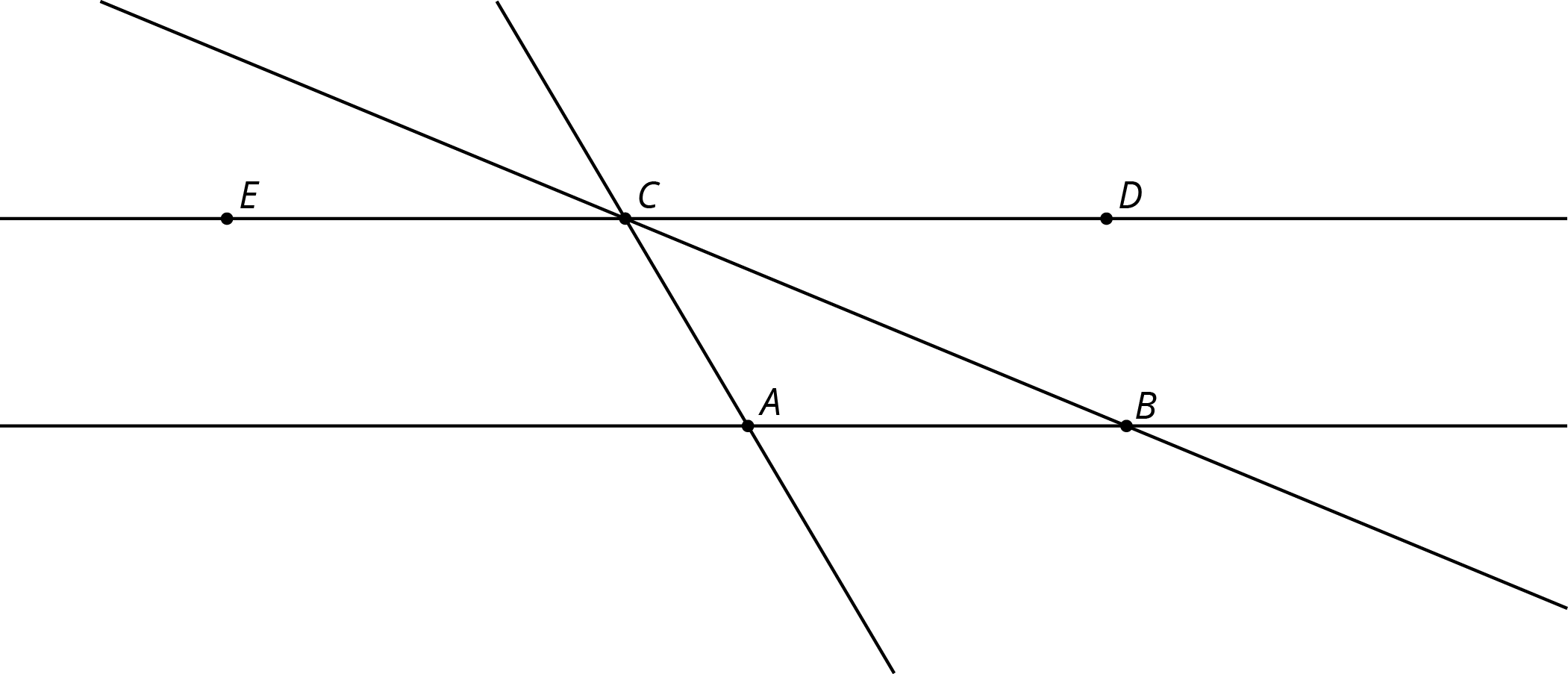
Four lines. Line A B. Line A C. Line C B. Line E D. Point C lies on line E D.

Angle \(ABC\) measures \(35^\circ\) and angle \(BAC\) measures \(115^\circ\).

  1. What is \(m{\angle ACE}\)?
  2. What is \(m{\angle DCB}\)?
  3. What is \(m{\angle ACB}\)?

Solution

For access, consult one of our IM Certified Partners.

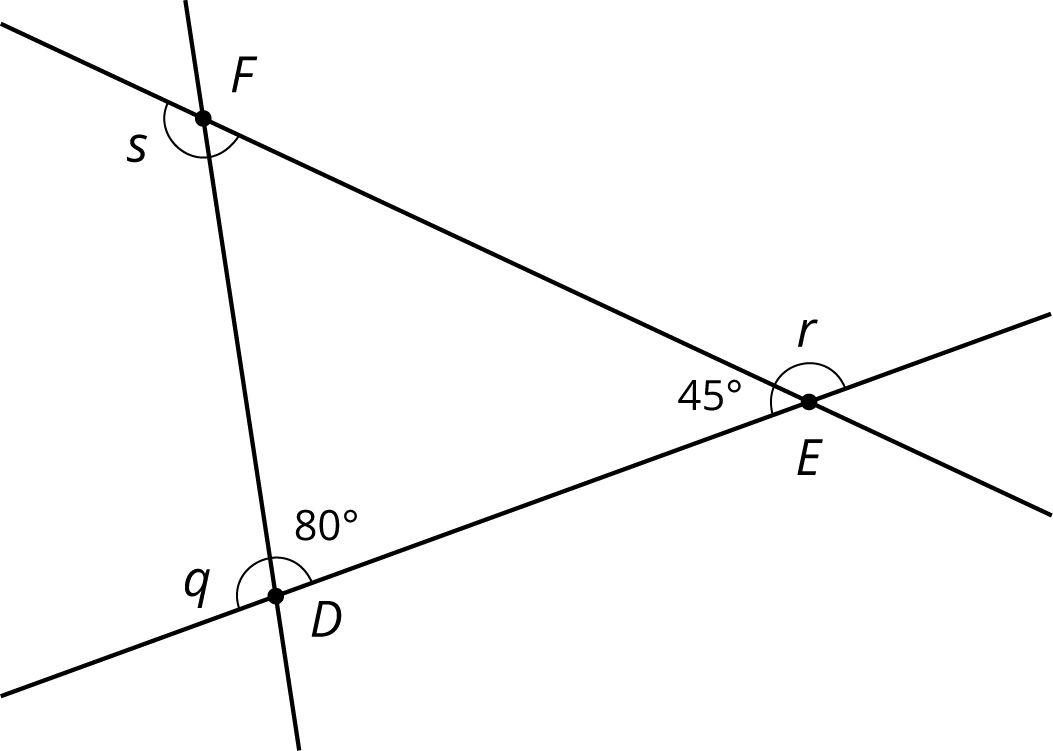
Problem 4

Here is a diagram of triangle \(DEF\).

  1. Find the measures of angles \(q\), \(r\), and \(s\).
  2. Find the sum of the measures of angles \(q\), \(r\), and \(s\).

  3. What do you notice about these three angles?

Three lines intersect to form Triangle D E F.

Solution

For access, consult one of our IM Certified Partners.

Problem 5

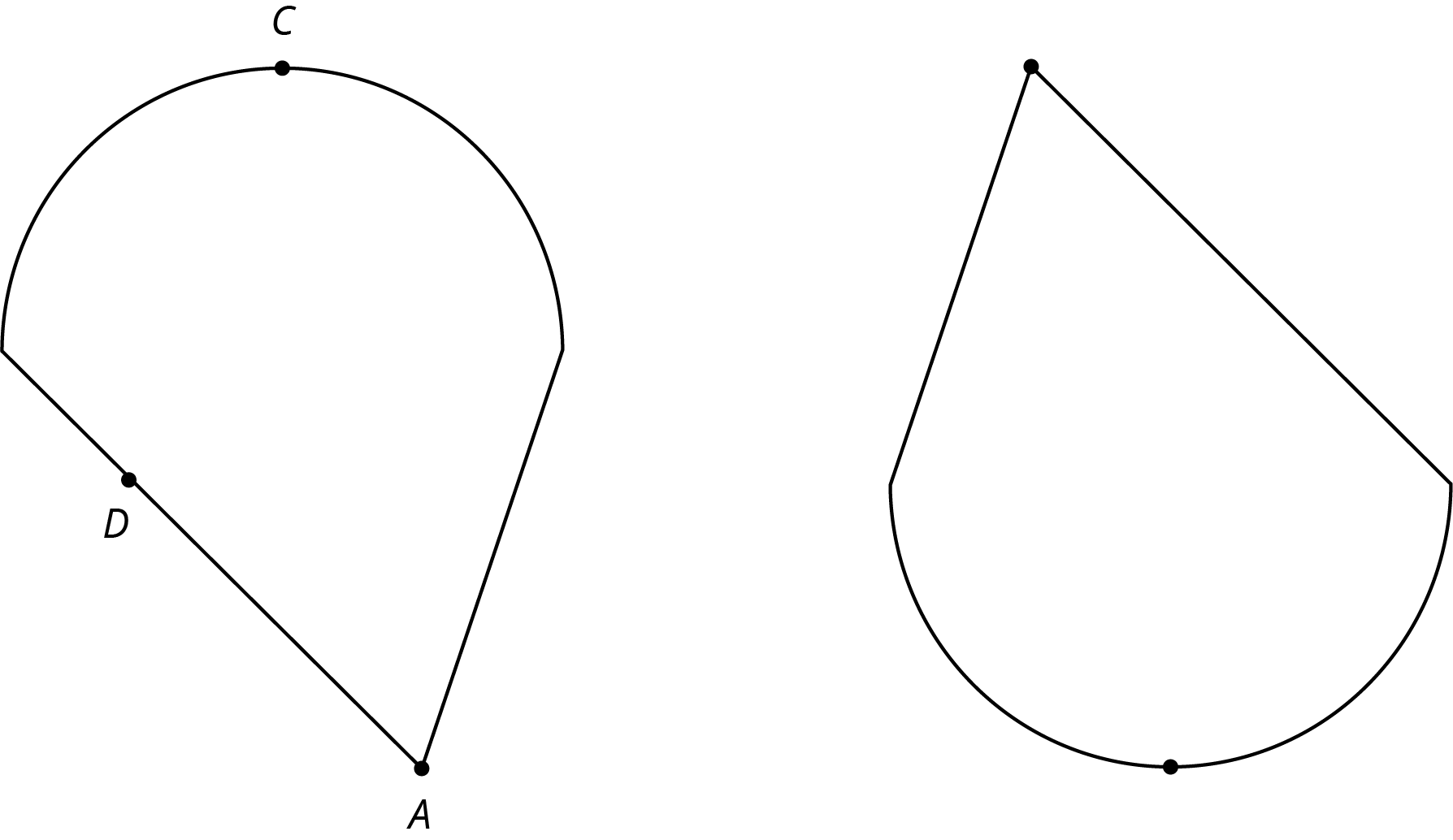
The two figures are congruent.

  1. Label the points \(A’\), \(B’\) and \(C’\) that correspond to \(A\), \(B\), and \(C\) in the figure on the right.
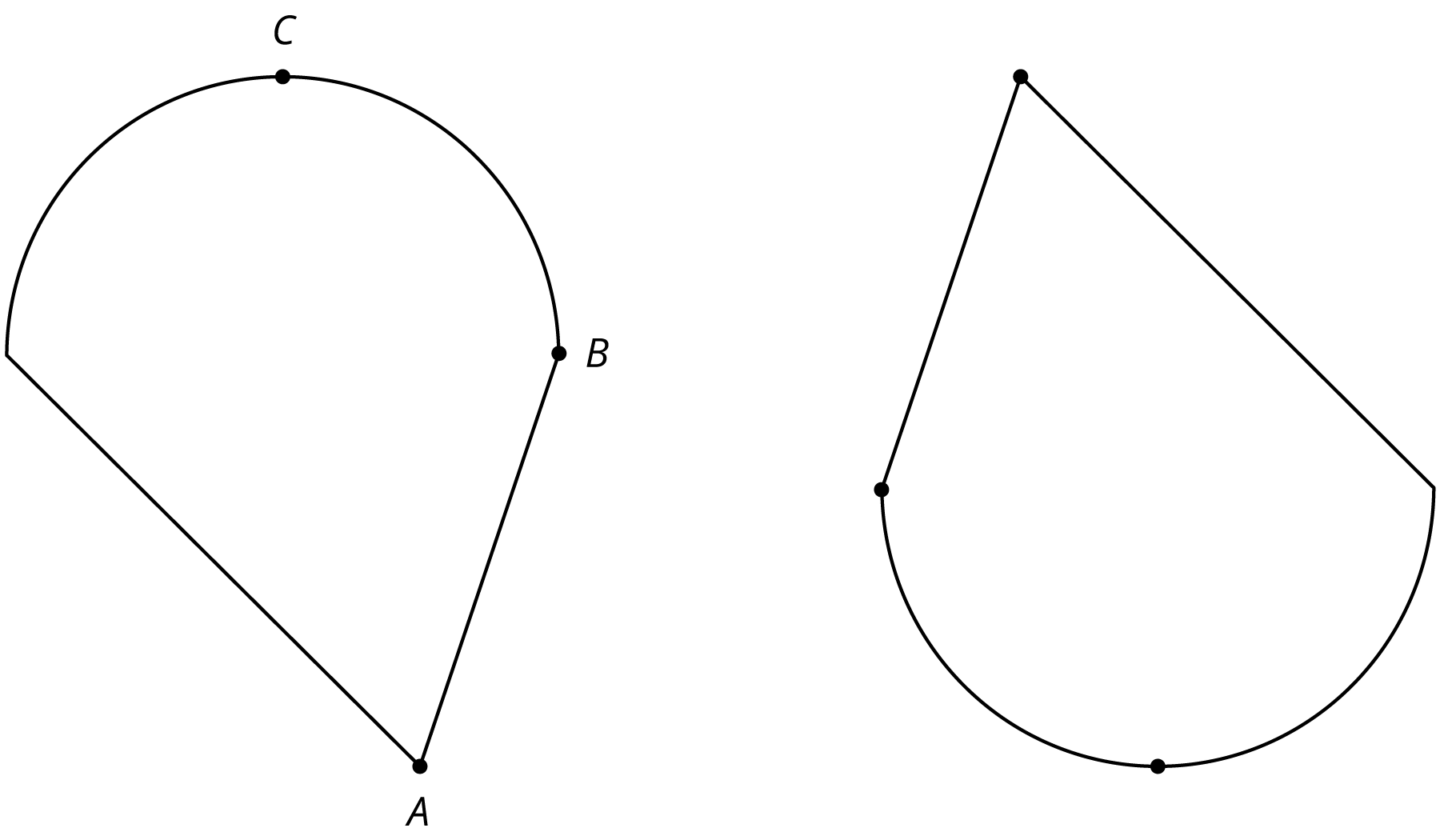
    Two congruent figures are semicircles with a connected opposite angle point.
  2. If segment \(AB\) measures 2 cm, how long is segment \(A’B’\)? Explain.
  3. The point \(D\) is shown in addition to \(A\) and \(C\). How can you find the point \(D’\) that corresponds to \(D\)? Explain your reasoning.
    Two congruent figures are semicircles with a connected opposite angle point.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 11.)