Lesson 4

The Mean

View Student Lesson

Problem 1

A preschool teacher is rearranging four boxes of playing blocks so that each box contains an equal number of blocks. Currently Box 1 has 32 blocks, Box 2 has 18, Box 3 has 41, and Box 4 has 9.

Select all the ways he could make each box have the same number of blocks.

A:

Remove all the blocks and make four equal piles of 25, then put each pile in one of the boxes.

B:

Remove 7 blocks from Box 1 and place them in Box 2.

C:

Remove 21 blocks from Box 3 and place them in Box 4.

D:

Remove 7 blocks from Box 1 and place them in Box 2, and remove 21 blocks from Box 3 and place them in Box 4.

E:

Remove 7 blocks from Box 1 and place them in Box 2, and remove 16 blocks from Box 3 and place them in Box 4.

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Three sixth-grade classes raised $25.50, $49.75, and $37.25 for their classroom libraries. They agreed to share the money raised equally. What is each class’s equal share? Explain or show your reasoning.

Solution

For access, consult one of our IM Certified Partners.

Problem 3

An earthworm farmer examined two containers of a certain species of earthworms so that he could learn about their lengths. He measured 25 earthworms in each container and recorded their lengths in millimeters.

Here are histograms of the lengths for each container.

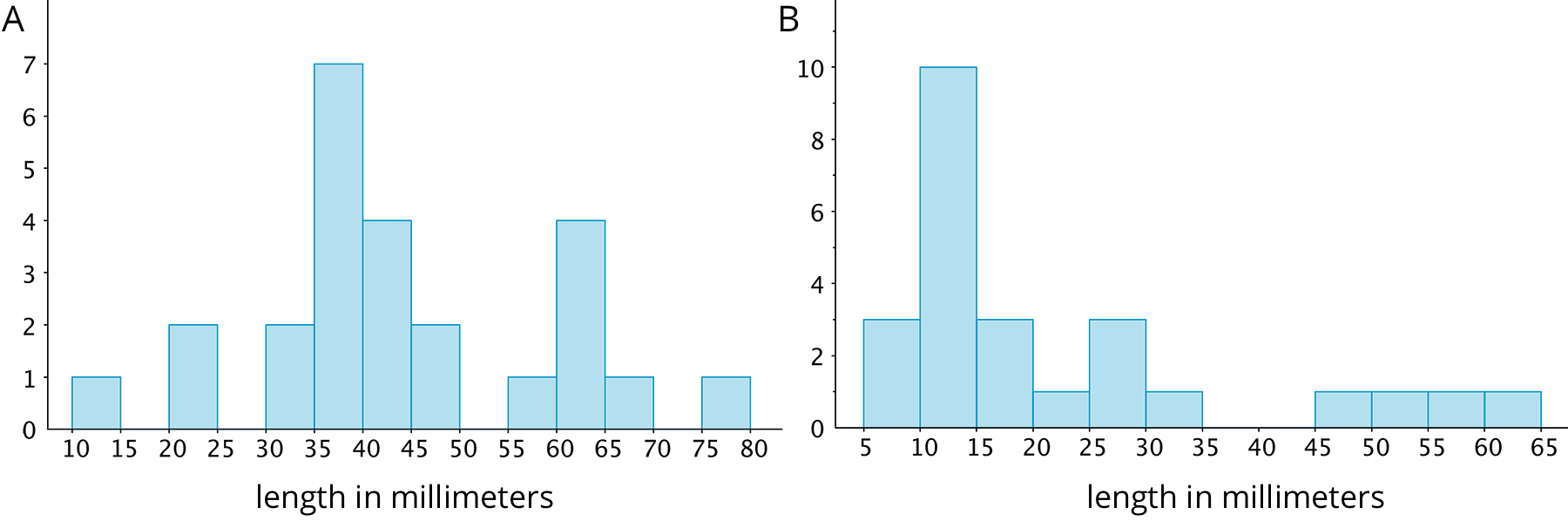
Two histograms. length in millimeters.
  1. Which container tends to have longer worms than the other container?
  2. For which container would 15 millimeters be a reasonable description of a typical length of the worms in the container?
  3. If length is related to age, which container had the most young worms?

Solution

For access, consult one of our IM Certified Partners.

(From Unit 8, Lesson 3.)

Problem 4

Noah scored 20 points in a game. Mai's score was 30 points. The mean score for Noah, Mai, and Clare was 40 points. What was Clare's score? Explain or show your reasoning.

Solution

For access, consult one of our IM Certified Partners.

Problem 5

  1. Plot \(\frac{2}{3}\) and \(\frac{3}{4}\) on a number line.

  2. Is \(\frac{2}{3} < \frac{3}{4}\), or is \(\frac{3}{4} < \frac{2}{3}\)? Explain how you know.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 7, Lesson 2.)

Problem 6

Select all the expressions that represent the total area of the large rectangle.

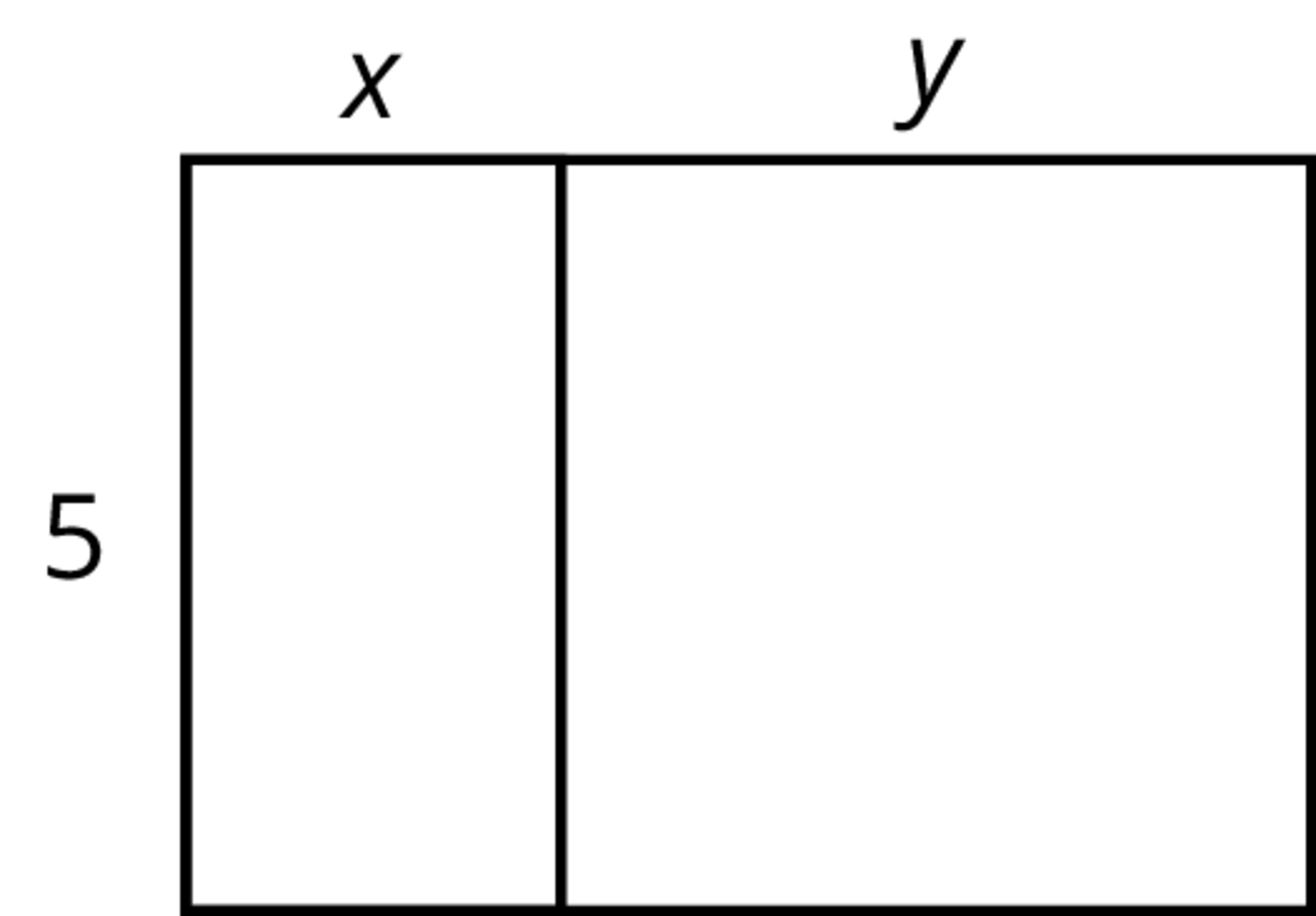
A large rectangle partitioned with a vertical line.
A:

\(5(x+y)\)

B:

\(5 + xy\)

C:

\(5x + 5y\)

D:

\(2(5+x + y)\)

E:

\(5xy\)

Solution

For access, consult one of our IM Certified Partners.

(From Unit 4, Lesson 10.)