Lesson 15
Keeping Track of All Possible Outcomes
15.1: How Many Different Meals? (5 minutes)
Warm-up
The purpose of this warm-up is to elicit methods students are already using to organize their understanding of different outcomes. In this lesson, students are asked to use different structures to think about the outcomes of experiments that involve multiple steps, so this activity should give you an idea of how students are approaching the problem on their own.
Launch
Arrange students in groups of 2. Tell students they should organize their work so it can be understood by others. Give students 1 minute of quiet think time, 3 minutes for partner discussion, and follow up with a whole-class discussion.
Student Facing
How many different meals are possible if each meal includes one main course, one side dish, and one drink?
| main courses | side dishes | drinks |
|---|---|---|
| grilled chicken | salad | milk |
| turkey sandwich | applesauce | juice |
| pasta salad | — | water |
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select several groups to share their methods for organizing their thoughts about the different meals that are possible.
Consider these questions for the discussion:
- “How did you know you counted all of the different possible meals?”
- “How did you know you didn’t repeat any meals?”
15.2: Lists, Tables, and Trees (15 minutes)
Activity
In this activity, students learn 3 different methods for writing the sample spaces of multi-step experiments and explore their use in a few different situations. Since the calculated probability of an event depends on the number of outcomes in the sample space, it is important to be able to find this value in an efficient way. In the discussion, students will explore how different methods may be useful in different situations (MP1).
As students work on the second set of questions, monitor for students who:
- Always use a list format to write out the sample space.
- Always use a tree format to write out the sample space.
- Change which representations they use for different questions.
Launch
Allow 5 minutes for students to answer the first set of questions, then pause the class to discuss the methods.
Poll the class for their favorite methods in the given situation and display the results for all to see. Ask at least 1 student for each representation for their reason they believe that method is their favorite.
Following the discussion, give students another 5 minutes of quiet work time to finish the questions. Follow with a whole-class discussion.
Design Principle(s): Support sense-making (for representation); Maximize meta-awareness
Student Facing
Consider the experiment: Flip a coin, and then roll a number cube.
Elena, Kiran, and Priya each use a different method for finding the sample space of this experiment.
-
Elena carefully writes a list of all the options: Heads 1, Heads 2, Heads 3, Heads 4, Heads 5, Heads 6, Tails 1, Tails 2, Tails 3, Tails 4, Tails 5, Tails 6.
- Kiran makes a table:
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| H | H1 | H2 | H3 | H4 | H5 | H6 |
| T | T1 | T2 | T3 | T4 | T5 | T6 |
-
Priya draws a tree with branches in which each pathway represents a different outcome:
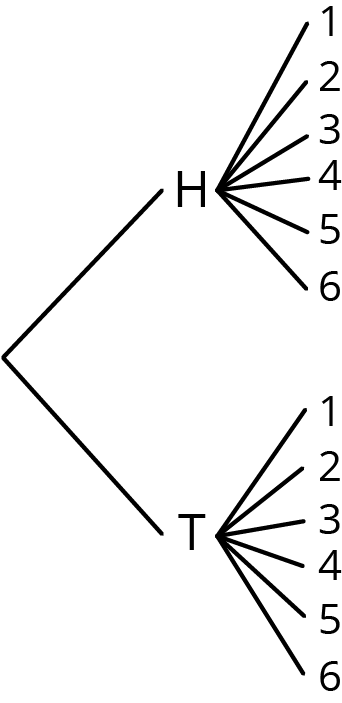
-
Compare the three methods. What is the same about each method? What is different? Be prepared to explain why each method produces all the different outcomes without repeating any.
-
Which method do you prefer for this situation?
Pause here so your teacher can review your work.
-
Find the sample space for each of these experiments using any method. Make sure you list every possible outcome without repeating any.
-
Flip a dime, then flip a nickel, and then flip a penny. Record whether each lands heads or tails up.
-
Han’s closet has: a blue shirt, a gray shirt, a white shirt, blue pants, khaki pants, and black pants. He must select one shirt and one pair of pants to wear for the day.
- Spin a color, and then spin a number.
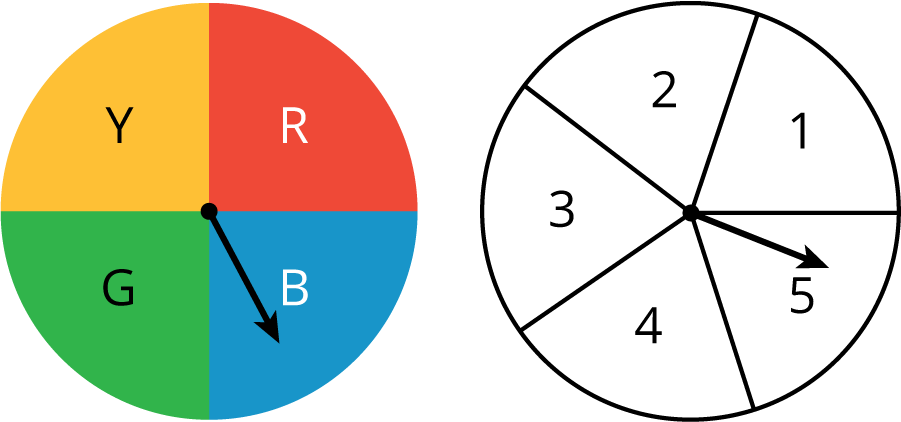
- Spin the hour hand on an analog clock, and then choose a.m. or p.m.
-
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may have trouble interpreting the tree diagram. Help students see that a single outcome is represented by following the “branches” from the point furthest to the left until they reach the end of a branch on the right side. It may help for students to write the full outcome on the diagram as well. In Priya’s picture, next to the uppermost 1, a student could write H1.
Activity Synthesis
The purpose of this discussion is to think about the different methods of writing the sample space and when each might be useful. The discussion is also meant to make the connection between the methods and the number of outcomes in the sample space so that students can quickly find the number of outcomes without writing out all the possibilities.
Select previously identified students to share their group’s strategies for answering the questions in the sequence identified in the Activity Narrative. For students who used the same representation throughout, ask, “Why did you choose to use this same strategy for all the questions? What are the benefits of this strategy? Did you encounter any problems using the strategy?” For students who changed strategies for different questions, ask, “How did you decide which strategy to use for each question?”
Consider these questions for the discussion:
- “What structure did you use for each situation to make sure all the different outcomes were included without duplicating any?”
- “Would each of Elena’s, Kiran’s, and Priya’s methods work for flipping the different coins?” (A table would not work since there are three parts.)
- “Count the number of outcomes in each sample space. Is there a way to find the number of outcomes without writing all the possibilities? Explain or show your reasoning.” (Note the connection of Kiran’s table structure of “2 rows of 6 outcomes” or Priya’s tree diagram of “2 groups of 6” to \(2 \boldcdot 6\) in the experiment where they flipped a coin and rolled a number cube.)
Supports accessibility for: Conceptual processing; Organization
15.3: How Many Sandwiches? (10 minutes)
Activity
In this activity, students practice using their understanding of ways to calculate the number of outcomes in the sample space without writing out the entire sample space (MP7). Many situations with multiple steps have very large sample spaces for which it is not helpful to write out the entire sample space, but it is still useful to know the number of outcomes in the sample space. In this activity, students find the number of different sandwiches that can be made from available options.
Launch
Explain to students that the sandwich makers are instructed to put a certain amount of each item on the sandwich for each selection. Therefore, if a person really loves tomatoes, he should ask for tomatoes twice as his two veggie choices. Give students 5 minutes of quiet work time followed by a whole-group discussion.
Supports accessibility for: Organization; Attention
Student Facing
-
A submarine sandwich shop makes sandwiches with one kind of bread, one protein, one choice of cheese, and two vegetables. How many different sandwiches are possible? Explain your reasoning. You do not need to write out the sample space.
- Breads: Italian, white, wheat
- Proteins: Tuna, ham, turkey, beans
- Cheese: Provolone, Swiss, American, none
- Vegetables: Lettuce, tomatoes, peppers, onions, pickles

- Andre knows he wants a sandwich that has ham, lettuce, and tomatoes on it. He doesn’t care about the type of bread or cheese. How many of the different sandwiches would make Andre happy?
-
If a sandwich is made by randomly choosing each of the options, what is the probability it will be a sandwich that Andre would be happy with?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Describe a situation that involves three parts and has a total of 24 outcomes in the sample space.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may attempt to write out the entire sample space. Encourage them to write a few outcomes to get the idea of what is possible, but let them know that the answer for question 1 is well over 1,000, so finding a pattern or way to calculate the answer might be more efficient.
Some students may not count the “none” option for cheese as a distinct choice. Show these students that a sandwich like “Italian bread, tuna, provolone, lettuce, and tomatoes” is different than a sandwich like “Italian bread, tuna, no cheese, lettuce, and tomatoes” and should be counted separately.
Some students may notice that the order of the vegetable selection may not matter. For example, selecting lettuce then tomato would create a similar sandwich to one with tomato then lettuce selected. Some sandwich shops may offer more of the first option, so we could ask students to consider the sandwiches as different based on this idea. Otherwise, there are only 720 sandwiches possible since there are only 15 different options for 2 vegetables and \(3 \boldcdot 4 \boldcdot 4 \boldcdot 15 = 720\).
Activity Synthesis
The purpose of the discussion is to help students understand the calculations behind the solutions of these problems.
Some questions for discussion:
- “Describe how the tree of sandwich options would look without drawing it out.” (The first column would have the 3 options for bread. Coming out from each of those options would be 4 branches for each of the proteins. From each of these there would be 4 more branches for each of the cheese options. Each of those would have 5 branches for the veggies. Finally, there would be 5 branches for the veggies again since the sandwich has 2 of them.)
- “How is the tree connected to the calculation of the size of the sample space?” (Since the first two choices [bread and protein] are 3 groups of 4 branches, there are 12 options for those two choices. When adding the cheese option, there are 12 groups of 4 or 48 options. For the first veggie, there are 48 groups of 5 things or 240 options. Finally, there are 240 groups of 5 veggies for the last option, giving a total of 1,200 outcomes.)
- “If the two veggie choices had to be different, would there be a higher or lower total number of possible sandwiches? Explain your reasoning.” (Fewer, since an item like “Italian bread, ham, Swiss, onions, and onions” was an option before, but is not an option with the new restriction.)
Design Principle(s): Support sense-making
Lesson Synthesis
Lesson Synthesis
Consider asking these discussion questions:
- “What are some methods for writing out the sample space of a chance experiment that consists of multiple steps?” (Trees, tables, and lists.)
- “How does the tree method relate to finding the number of outcomes in a sample space?” (Each path from the start to the end of the “branches” represents one outcome in the sample space, so counting all the paths will give you the number of items in the sample space.)
- “Why is it important to know the number of outcomes in a sample space when finding probability?” (Probability can be found by \(\frac{k}{n}\) where \(k\) represents the number of outcomes in the event and \(n\) represents the number of outcomes in the sample space.)
15.4: Cool-down - Random Points (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Sometimes we need a systematic way to count the number of outcomes that are possible in a given situation. For example, suppose there are 3 people (A, B, and C) who want to run for the president of a club and 4 different people (1, 2, 3, and 4) who want to run for vice president of the club. We can use a tree, a table, or an ordered list to count how many different combinations are possible for a president to be paired with a vice president.
With a tree, we can start with a branch for each of the people who want to be president. Then for each possible president, we add a branch for each possible vice president, for a total of \(3\boldcdot 4 = 12\) possible pairs. We can also start by counting vice presidents first and then adding a branch for each possible president, for a total of \(3 \boldcdot 4 = 12\) possible pairs.
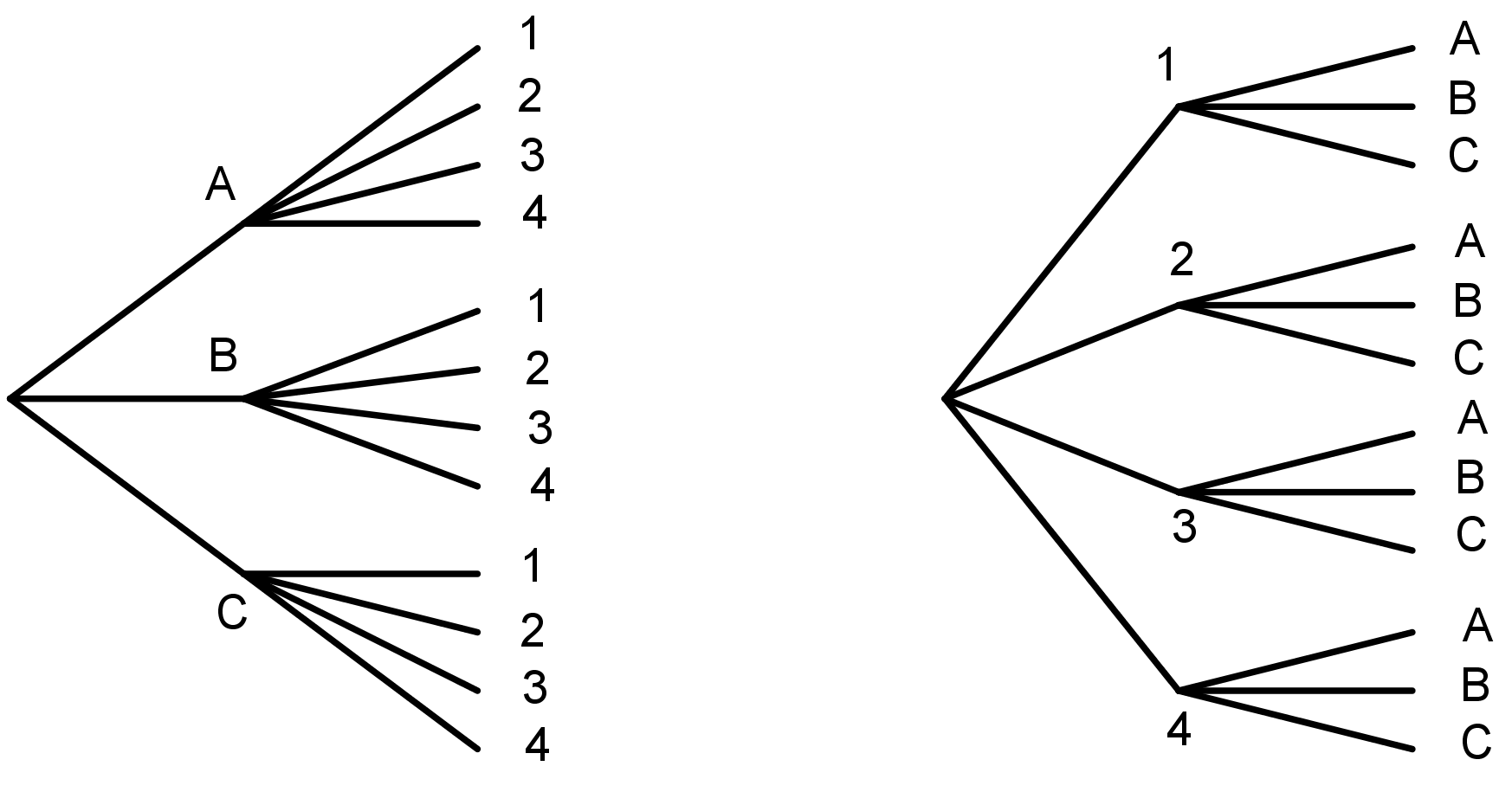
A table can show the same result:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| A | A, 1 | A, 2 | A, 3 | A, 4 |
| B | B, 1 | B, 2 | B, 3 | B, 4 |
| C | C, 1 | C, 2 | C, 3 | C, 4 |
So does this ordered list:
A1, A2, A3, A4, B1, B2, B3, B4, C1, C2, C3, C4