Lesson 2

Comparing Positive and Negative Numbers

View Student Lesson

Lesson Narrative

Returning to the temperature context, students compare rational numbers representing temperatures and learn to write inequality statements that include negative numbers. Students then consider rational numbers in all forms (fractions, decimals) and learn to compare them by plotting on a number line and considering their relative positions. Students abstract from “hotter” and “colder” to “greater” and “less,” so if a number \(a\) is to the right of a number \(b\), we can write the inequality statements \(a>b\) and \(b<a\). Students also find that the greatest number is not always the one farthest from zero, which was the case before students encountered negative numbers. For example, -100 is much farther away from zero than \(\text-\frac{1}{100}\), but since \(\text-\frac{1}{100}\) is to the right of -100, it is larger and we can write \(\text-\frac{1}{100}>\text-100\). Students are briefly introduced to the word sign (i.e., algebraic sign) since it is often used to talk about whether numbers are positive or negative. They also reason about opposites, which are numbers that are on opposite sides of 0 but the same distance from zero. Students use the structure of the number line to reason about relationships between numbers (MP7).

Learning Goals

Teacher Facing

  • Compare rational numbers in the context of temperature or elevation, and express the comparisons (in writing) using the symbols > and <.>
  • Comprehend that two numbers are called “opposites” when they are the same distance from zero, but on different sides of the number line.
  • Comprehend the word “sign” (in spoken language) to refer to whether a number is positive or negative.
  • Critique (orally and in writing) statements comparing rational numbers, including claims about relative position and claims about distance from zero.

Student Facing

Let’s compare numbers on the number line.

Learning Targets

Student Facing

  • I can explain how to use the positions of numbers on a number line to compare them.
  • I can explain what a rational number is.
  • I can use inequalities to compare positive and negative numbers.
  • I understand what it means for numbers to be opposites.

CCSS Standards

Building On

Addressing

Building Towards

Glossary Entries

  • opposite

    Two numbers are opposites if they are the same distance from 0 and on different sides of the number line.

    For example, 4 is the opposite of -4, and -4 is the opposite of 4. They are both the same distance from 0. One is negative, and the other is positive.

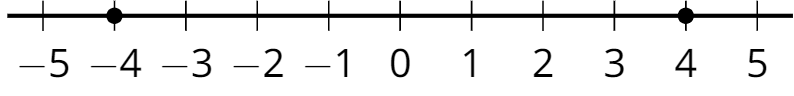
    Number line that extends from -5 to 5, with points at -4 and 4.
  • rational number

    A rational number is a fraction or the opposite of a fraction.

    For example, 8 and -8 are rational numbers because they can be written as \(\frac81\) and \(\text-\frac81\).

    Also, 0.75 and -0.75 are rational numbers because they can be written as \(\frac{75}{100}\) and \(\text-\frac{75}{100}\).

  • sign

    The sign of any number other than 0 is either positive or negative.

    For example, the sign of 6 is positive. The sign of -6 is negative. Zero does not have a sign, because it is not positive or negative.

Print Formatted Materials

For access, consult one of our IM Certified Partners.

Additional Resources

Google Slides

For access, consult one of our IM Certified Partners.
PowerPoint Slides

For access, consult one of our IM Certified Partners.