Lesson 3

Ordering Rational Numbers

3.1: How Do They Compare? (10 minutes)

The purpose of this warm-up is for students to review strategies for comparing whole numbers, decimal numbers, and fractions as well as the use of inequality symbols. The numbers in each pair have been purposefully chosen based on misunderstandings students typically have when comparing. Since there are many pairs of numbers to compare, it may not be possible to share all of the students’ strategies for each pair. Consider sharing only one strategy for each pair if all of the students agree and more than one if there is a disagreement among the students.

Give students 3 minutes of quiet work time followed by a whole-class discussion.

Use the symbols >, <, or = to compare each pair of numbers. Be prepared to explain your reasoning.

12 _____ 19

212 _____ 190

15 _____ 1.5

9.02 _____ 9.2

6.050 _____ 6.05

0.4 _____ $\frac{9}{40}$

$\frac{19}{24}$ _____ $\frac{19}{21}$

$\frac{16}{17}$ _____ $\frac{11}{12}$

For access, consult one of our IM Certified Partners.

Some students may not remember the inequality symbols that represent the phrases: greater than, less than, and equal to. Show these students each of the inequality symbols in an example that they can refer back to as they work.

For each pair of numbers, ask one or two students to share their reasoning. Record and display their reasoning for all to see. If the whole class agrees, move on to the next question, but if there is a disagreement, ask students to explain their thinking until an agreement is reached. If possible, spend more time on the questions with numbers expressed with decimals and fractions.

3.2: Ordering Rational Number Cards (15 minutes)

In this activity, students order rational numbers from least to greatest in 2 steps. They first order positive rational numbers, and then negative ones. The numbers are written as fractions, decimals, and integers. By manipulating physical cards, students get a tangible sense of how rational numbers relate to each other.

Notice conversations students have when deciding how to place fractions and decimals, especially on the negative side of the number line. Pay attention to proper use and understanding of “less” or “greater,” and improper use of “bigger” or “smaller.” One strategy to look for is fitting new numbers between known numbers (e.g., $\text-\frac98$ is between -1 and -2).

Arrange students in groups of 2. Distribute the first set of cards to each group. Give students 5 minutes to order the first set of cards, taking turns to place each number. When a group finishes ordering, check their ordering before giving them the second set of cards. To speed up the checking process, consider referring groups finishing the first set to compare their ordering to a group you have already checked. Give students 5 minutes to order the second set of cards followed by whole-class discussion. When collecting the cards, ask groups to separate the negative set of numbers and randomize each set for the next class.

Representation: Internalize Comprehension. Chunk this task into more manageable parts to differentiate the degree of difficulty or complexity by beginning with fewer cards. For example, give students a subset of the cards to start with and introduce the remaining cards once students have placed their initial cards in the correct order.
Supports accessibility for: Conceptual processing; Organization

Your teacher will give you a set of number cards. Order them from least to greatest.

Your teacher will give you a second set of number cards. Add these to the correct places in the ordered set.

For access, consult one of our IM Certified Partners.

Some students may place negative numbers in order of increasing absolute value on the left side of 0. Ask these students to draw a number line that goes 5 units right and 5 units left of 0. Point out that negative numbers progress as -1, -2, -3, -4, -5 as they move outward from 0.

The purpose of the discussion is to solidify students’ understanding of the order of rational numbers. Select previously identified students to share how they decided how to place numbers like $\text-\frac98$, $\frac98$, $\frac83$, and $\text-22\frac12$. Here are some questions to consider:

Which numbers were hardest to place and which were the least difficult?
How does placing negative numbers compare to placing positive numbers?
How did you use numbers you had already placed to reason about where to place new numbers?

Speaking: MLR2 Collect and Display. During the class discussion record words and phrases that students use to explain how to order negative numbers. Highlight phrases that include a reference to “greater than,” “less than,” “to the right of” and “to the left of.” As a class, discuss how to order -23, -22 and one half, and -22. Record student words on a visual display of a number line. This will help students read and use mathematical language during future coursework.
Design Principle(s): Support sense-making

3.3: Comparing Points on A Line (15 minutes)

Students practice using relational language “greater than” and “less than” to describe order and position on number line.

Arrange students in groups of 2. Give students 7 minutes of quiet work time for both problems before 3–5 minutes for partner discussion, followed by whole-class discussion.

Representation: Internalize Comprehension. Activate or supply background knowledge. Some students may benefit from access to blank or partially completed number lines for the final question.
Supports accessibility for: Visual-spatial processing; Organization

Speaking, Listening: MLR8 Discussion Supports. To support students to produce statements with justification during the conversation between partners, provide student sentence frames such as “____ is greater than ____ because ____.” ; “____ is the opposite of ____ because ____.” ; “I know that ____ is a negative number because _____.”
Design Principle(s): Optimize output (for justification)

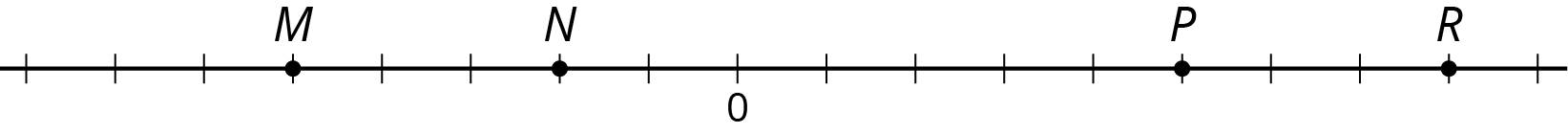
Use each of the following terms at least once to describe or compare the values of points $M$, $N$, $P$, $R$.
- greater than
- less than
- opposite of (or opposites)
- negative number
Tell what the value of each point would be if:
1. $P$ is $2\frac12$
2. $N$ is -0.4
3. $R$ is 200
4. $M$ is -15

For access, consult one of our IM Certified Partners.

Are you ready for more?

The list of fractions between 0 and 1 with denominators between 1 and 3 looks like this:

$ \frac{0}{1}, \, \frac{1}{1},\, \frac{1}{2},\, \frac{1}{3},\, \frac{2}{3}$

We can put them in order like this: $ \frac{0}{1} < \frac{1}{3} < \frac{1}{2} < \frac{2}{3} < \frac{1}{1}$

Now let’s expand the list to include fractions with denominators of 4. We won’t include $\frac{2}{4}$, because $\frac{1}{2}$ is already on the list.

$ \frac{0}{1} <\frac{1}{4} < \frac{1}{3} < \frac{1}{2} < \frac{2}{3} < \frac{3}{4} < \frac{1}{1}$

Expand the list again to include fractions that have denominators of 5.
Expand the list you made to include fractions have have denominators of 6.
When you add a new fraction to the list, you put it in between two “neighbors.” Go back and look at your work. Do you see a relationship between a new fraction and its two neighbors?

For access, consult one of our IM Certified Partners.

The purpose for discussion is to give students the opportunity to use precise language as they compare the relative positions of rational numbers. Give students 3–5 minutes to discuss their responses with a partner before whole-class discussion. Ask students to share their partner’s reasoning, especially if it was different than their own. Here are some questions to consider for whole-class discussion:

“Did you ever have a different answer than your partner? If so, were you both correct? If not, how did you work to reach agreement?”
“How did your partner decide the value of each unit on the number line in problem 2? Did you think of it a different way?”
“How can we tell if two numbers are opposites?” (They are the same distance from 0.)
“How can we tell if one number is greater or less than another number?” (Numbers toward the right are considered greater, and numbers toward the left are considered less.)

3.4: Drinks for Sale (15 minutes)

Students interpret positive and negative numbers in the context of a changing inventory (MP2).

Teacher Notes for IM 6–8 Accelerated

This activity is optional. Students are introduced to conventions for using signed numbers to represent money spent and received, as well as inventory gained and lost.

Keep students in the same groups of 2. Give students 8 minutes of quiet work time and 3 minutes of partner discussion. Follow with whole-class discussion.

A vending machine in an office building sells bottled beverages. The machine keeps track of all changes in the number of bottles from sales and from machine refills and maintenance. This record shows the changes for every 5-minute period over one hour.

What might a positive number mean in this context? What about a negative number?
What would a “0” in the second column mean in this context?
Which numbers—positive or negative—result in fewer bottles in the machine?
At what time was there the greatest change to the number of bottles in the machine? How did that change affect the number of remaining bottles in the machine?
At which time period, 8:05–8:09 or 8:25–8:29, was there a greater change to the number of bottles in the machine? Explain your reasoning.
The machine must be emptied to be serviced. If there are 40 bottles in the machine when it is to be serviced, what number will go in the second column in the table?

time	number of bottles
8:00–8:04	-1
8:05–8:09	+12
8:10–8:14	-4
8:15–8:19	-1
8:20–8:24	-5
8:25–8:29	-12
8:30–8:34	-2
8:35–8:39	0
8:40–8:44	0
8:45–8:49	-6
8:50–8:54	+24
8:55–8:59	0
service

For access, consult one of our IM Certified Partners.

Are you ready for more?

Priya, Mai, and Lin went to a cafe on a weekend. Their shared bill came to \$25. Each student gave the server a \$10 bill. The server took this \$30 and brought back five \$1 bills in change. Each student took \$1 back, leaving the rest, \$2, as a tip for the server.

As she walked away from the cafe, Lin thought, “Wait—this doesn’t make sense. Since I put in \$10 and got \$1 back, I wound up paying \$9. So did Mai and Priya. Together, we paid \$27. Then we left a \$2 tip. That makes \$29 total. And yet we originally gave the waiter \$30. Where did the extra dollar go?”

Think about the situation and about Lin’s question. Do you agree that the numbers didn’t add up properly? Explain your reasoning.

For access, consult one of our IM Certified Partners.

The goal of the discussion is to allow students to share their thoughts on the meaning of positive and negative numbers in context. Ask students to share their responses with their partner and work to reach agreement. Monitor groups’ discussions and select students to share their partner’s reasoning about what the numbers in the table mean. Ask students to summarize the story the numbers in the table tell. Tell students that tables like this (but perhaps more complicated) are used all the time to tell stories about what is happening in the world.

Speaking, Listening: MLR2 Collect and Display. To highlight words students use while speaking about positive and negative numbers, record on a visual display common or important phrases you hear students say related to the values in the table (e.g., “put into the machine”, “added to the machine”, “taken out”, “removed”). Make sure to include informal descriptions as well as more precise language. This will help students connect the everyday language that is used in mathematical situation to the more precise academic language.
Design Principle(s): Support sense-making

Lesson Synthesis

Ask students to summarize the ideas they have developed in the last few lessons about plotting and comparing rational numbers. Here are some questions to consider:

“What are some situations where negative numbers make sense? What do the words ‘positive,’ ‘negative,’ and 0 mean in those situations?” (Elevation: 0 represents sea level, negative represents below sea level, and positive represents above sea level. Temperature: $0^\circ \text{C}$ represents the standard freezing point of water, positive represents temperatures warmer than freezing, and negative represents temperatures below freezing.)
“What about on the number line? What do ‘positive’ and ‘negative’ mean on the number line? Is 0 positive or negative?” (Negative numbers are numbers left of 0 on the number line, and positive numbers are to the right of 0. The number 0 is neither positive nor negative.)
“What are some ideas you have about ‘opposites?’ What is the opposite of 0?” (Opposites are numbers that are the same distance from 0. They come in pairs—one positive, one negative—except for 0, which is its own opposite.)
“How can you tell if one number is greater than or less than another? How do you write it?” (Given two rational numbers, the number toward the right on the number line is considered “greater,” and the number toward the left is considered “less.” We use the $<$ and $>$ symbols to indicate “less than” and “greater than,” respectively.)

3.5: Cool-down - Getting Them in Order (5 minutes)

For access, consult one of our IM Certified Partners.

Student Lesson Summary

To order rational numbers from least to greatest, we list them in the order they appear on the number line from left to right. For example, we can see that the numbers

-2.7, -1.3, 0.8

are listed from least to greatest because of the order they appear on the number line.

Number line, negative 3 to 3 by ones. Above the line, points are indicated at negative 2 point 7, negative 1 point 3, zero point 8.

Lesson 3

3.1: How Do They Compare? (10 minutes)

Warm-up

Launch

Student Facing

Student Response

Anticipated Misconceptions

Activity Synthesis

3.2: Ordering Rational Number Cards (15 minutes)

Activity

Launch

Student Facing

Student Response

Anticipated Misconceptions

Activity Synthesis

3.3: Comparing Points on A Line (15 minutes)

Activity

Launch

Student Facing

Student Response

Student Facing

Are you ready for more?

Student Response

Activity Synthesis

3.4: Drinks for Sale (15 minutes)

Activity

Launch

Student Facing

Student Response

Student Facing

Are you ready for more?

Student Response

Activity Synthesis

Lesson Synthesis

Lesson Synthesis

3.5: Cool-down - Getting Them in Order (5 minutes)

Cool-Down

Student Lesson Summary

Student Facing