Lesson 4
Comparing Relationships with Tables
4.1: Adjusting a Recipe (5 minutes)
Warm-up
This activity encourages students to reason about equivalent ratios in a context. During the discussion, emphasize the use of ratios and proportions in determining the effect on the taste of the lemonade.
Launch
Arrange students in groups of 2. Give students 2 minutes of quiet think time.
Optionally, instead of the abstract recipe description, you could bring in a clear glass, measuring implements, and the lemonade ingredients. Pour in the ingredients and introduce the task that way.
Student Facing
A lemonade recipe calls for the juice of 5 lemons, 2 cups of water, and 2 tablespoons of honey.
Invent four new versions of this lemonade recipe:
- One that would make more lemonade but taste the same as the original recipe.
- One that would make less lemonade but taste the same as the original recipe.
- One that would have a stronger lemon taste than the original recipe.
- One that would have a weaker lemon taste than the original recipe.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite students to share their versions of the recipe with the class and record them for all to see. After each explanation, ask the class if they agree or disagree and how the new lemonade would taste. After recording at least 3 responses for each, ask students to describe any patterns they notice how the recipe was adjusted. If students do not mention ratios in their descriptions, be sure to ask them how the ratios changed in their new recipe.
4.2: Visiting the State Park (15 minutes)
Activity
This activity provides the first example in this unit of a relationship that is not proportional. The second question focuses students’ attention on the unit rates. If the relationship were proportional then regardless of the number of people in a vehicle, the cost per person would be the same. The question about the bus is to show students that they can’t just scale up from 10. Students who write an equation also see that it is not of the form \(y = kx\). In a later lesson students will learn that only equations of this form represent proportional relationships.
Monitor for students who approached this problem using different representations.
Launch
Keep students in the same groups of 2. Give 5 minutes of quiet work time, followed by 5 minutes of students discussing responses with a partner, followed by a whole-class discussion.
Supports accessibility for: Memory; Organization
Student Facing
Entrance to a state park costs $6 per vehicle, plus $2 per person in the vehicle.
- How much would it cost for a car with 2 people to enter the park? 4 people? 10 people? Record your answers in the table.
number of
people in vehicletotal entrance cost
in dollars2 4 10 - For each row in the table, if each person in the vehicle splits the entrance cost equally, how much will each person pay?
- How might you determine the entrance cost for a bus with 50 people?
- Is the relationship between the number of people and the total entrance cost a proportional relationship? Explain how you know.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
What equation could you use to find the total entrance cost for a vehicle with any number of people?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
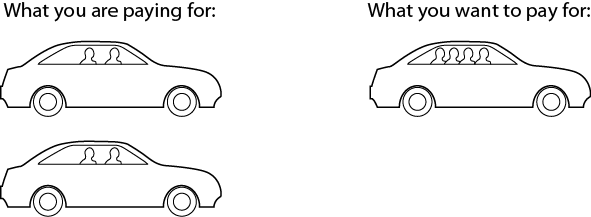
Some students may not account for the cost of the vehicle. They will get the following table with incorrect values and will need to be prompted to include the cost of the vehicle.
| number of people in vehicle |
total entrance cost in dollars |
|---|---|
| 2 | \$10 |
| 4 | \$20 |
| 10 | \$50 |
Teachers will want to circulate around the room keeping an eye out for this mistake and address it as soon as possible so that students spend most of their work time analyzing the non-proportional relationship. These diagrams may be helpful in illustrating to them that their resulting prices are including more than one vehicle. This gives them an opportunity to make sense of problems and persevere in solving them (MP1).
Activity Synthesis
Select students to explain why they think the relationship is or is not proportional. Reasons they may give:
- The cost per person is different for different number of people in a vehicle, i.e. the quotients of the entries in each row are not equal for all rows of the table.
- The ratio of people in the vehicle to total entrance cost are not equivalent ratios. You can't just multiply the entries in one row by the same constant to get the entries in another row.
- Each number of people and corresponding total entrance cost is not characterized by the same unit rate. You can't multiply the entries in the first column by the same number (constant of proportionality) to get the numbers in the second column.
Students who found an equation will also note that the equation is not of the same form as other equations, but they can’t use this as a criterion until the class has established that only equations of this form represent proportional relationships. (This part of the discussion should come at the end of the next lesson, after students have analyzed lots of different equations.)
4.3: Running Laps (15 minutes)
Activity
The purpose of this activity is to understand that discrete values in a table can be used as evidence that a relationship is proportional and can be used to know for sure that a relationship is not proportional, but can’t be used to know for sure whether a relationship is definitely proportional. This activity builds on previous ones involving constant speed, but analyzes pace (minutes per lap) rather than speed (laps per minute). Explaining why the information given in the table is enough to conclude that Han didn't run at a constant pace but is not enough to know for sure whether Clare ran at a constant pace requires students to make a viable argument (MP3).
Launch
Keep students in the same groups of 2. Give 5 minutes of quiet work time, followed by 5 minutes of students discussing responses with a partner, followed by a whole-class discussion.
Design Principle(s): Maximize meta-awareness; Support sense-making
Student Facing
Han and Clare were running laps around the track. The coach recorded their times at the end of laps 2, 4, 6, and 8.
Han's run:
| distance (laps) | time (minutes) | minutes per lap |
|---|---|---|
| 2 | 4 | |
| 4 | 9 | |
| 6 | 15 | |
| 8 | 23 |
Clare's run:
| distance (laps) | time (minutes) | minutes per lap |
|---|---|---|
| 2 | 5 | |
| 4 | 10 | |
| 6 | 15 | |
| 8 | 20 |
- Is Han running at a constant pace? Is Clare? How do you know?
- Write an equation for the relationship between distance and time for anyone who is running at a constant pace.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students are likely to answer that Clare is running at a constant pace because the minutes per lap shown in the table are the same for each lap. Because we only have four data points in a table, spaced at 5-minute intervals, Clare could still be speeding up and slowing down between the recorded times. However, given the data, it is reasonable to assume Clare is running at a constant pace for the purpose of estimating times or distances.
Activity Synthesis
Invite students to explain why they think each person is or is not running at a constant pace. Point out to students that although the data points in the table for Clare are pairs in a proportional relationship, these four pairs of values do not guarantee that Clare ran at a constant pace. She might have, but we don't know if she was running at a constant pace between the times that the coach recorded.
Ask the following questions:
- "Can you represent either relationship with an equation?" (The answer for Han is “no” and the answer for Clare is “yes, if she really ran at a constant pace between the points in time when the times were recorded.” Write the equation for Clare together: \(t = 2.5 d\).)
- “Are the pairs of values in the table for Clare's run still values from a proportional relationship if we calculate laps per minute instead of minutes per lap? How does that change the equation?” (Yes, \(d = 0.4 t\).)
Lesson Synthesis
Lesson Synthesis
In this lesson, we learned some ways to tell whether a table could represent a proportional relationship. Revisit one or more of the activities in the lesson, highlighting the following points:
- If the quotient is the same for each row in the table, the table could represent a proportional relationship.
- It can be helpful to compute and write down this quotient for each row.
- The quotient is the constant of proportionality for the relationship (if the relationship is proportional).
- If all the quotients are not the same, the table definitely does not represent a proportional relationship.
- The relationship between the two quantities in a proportional relationship can be expressed using an equation of the form \(y=kx\).
4.4: Cool-down - Apples and Pizza (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Here are the prices for some smoothies at two different smoothie shops:
Smoothie Shop A
| smoothie size (oz) |
price ($) |
dollars per ounce |
|---|---|---|
| 8 | 6 | 0.75 |
| 12 | 9 | 0.75 |
| 16 | 12 | 0.75 |
| \(s\) | \(0.75s\) | 0.75 |
Smoothie Shop B
| smoothie size (oz) |
price ($) |
dollars per ounce |
|---|---|---|
| 8 | 6 | 0.75 |
| 12 | 8 | 0.67 |
| 16 | 10 | 0.625 |
| \(s\) | ??? | ??? |
For Smoothie Shop A, smoothies cost \$0.75 per ounce no matter which size we buy. There could be a proportional relationship between smoothie size and the price of the smoothie. An equation representing this relationship is \(\displaystyle p=0.75 s\) where \(s\) represents size in ounces and \(p\) represents price in dollars. (The relationship could still not be proportional, if there were a different size on the menu that did not have the same price per ounce.)
For Smoothie Shop B, the cost per ounce is different for each size. Here the relationship between smoothie size and price is definitely not proportional.
In general, two quantities in a proportional relationship will always have the same quotient. When we see some values for two related quantities in a table and we get the same quotient when we divide them, that means they might be in a proportional relationship—but if we can't see all of the possible pairs, we can't be completely sure. However, if we know the relationship can be represented by an equation is of the form \(y = k x\), then we are sure it is proportional.