Lesson 10

Rectangles and Triangles with Fractional Lengths

View Student Lesson

Problem 1

  1. Find the unknown side length of the rectangle if its area is 11 m2. Show your reasoning.
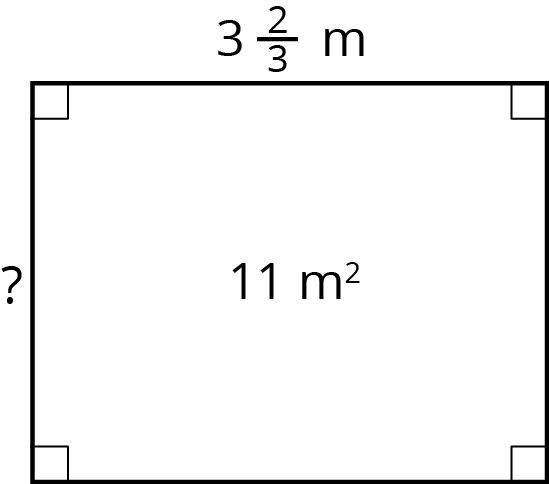
    A rectangle. 
  2. Check your answer by multiplying it by the given side length (\(3\frac 23\)). Is the resulting product 11? If not, revise your previous work.

Solution

For access, consult one of our IM Certified Partners.

Problem 2

A worker is tiling the floor of a rectangular room that is 12 feet by 15 feet. The tiles are square with side lengths \(1\frac13\) feet. How many tiles are needed to cover the entire floor? Show your reasoning.

 

Solution

For access, consult one of our IM Certified Partners.

Problem 3

The area of a rectangle is \(17\frac12\) in2 and its shorter side is \(3\frac12\) in. Draw a diagram that shows this information. What is the length of the longer side?

Solution

For access, consult one of our IM Certified Partners.

Problem 4

The triangle has an area of \(7\frac{7}{8}\) cm2 and a base of \(5\frac14\) cm.

What is the length of \(h\)? Explain your reasoning.

A triangle. 

Solution

For access, consult one of our IM Certified Partners.

Problem 5

Find the value of \(\frac{5}{32}\div \frac{25}{4}\). Show your reasoning.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 3, Lesson 7.)

Problem 6

A builder is building a fence with \(6\frac14\)-inch-wide wooden boards, arranged side-by-side with no gaps or overlaps. How many boards are needed to build a fence that is 150 inches long? Show your reasoning.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 3, Lesson 9.)