Lesson 17

Drawing Triangles

Let’s see how many different triangles we can draw with certain measurements.

Problem 1

Use a protractor to try to draw each triangle. Which of these three triangles is impossible to draw?

  1. A triangle where one angle measures \(20^\circ\) and another angle measures \(45^\circ\)
  2. A triangle where one angle measures \(120^\circ\) and another angle measures \(50^\circ\)

  3. A triangle where one angle measures \(90^\circ\) and another angle measures \(100^\circ\)

Problem 2

A triangle has an angle measuring \(90^\circ\), an angle measuring \(20^\circ\), and a side that is 6 units long. The 6-unit side is in between the \(90^\circ\) and \(20^\circ\) angles.

  1. Sketch this triangle and label your sketch with the given measures.
  2. How many unique triangles can you draw like this?

Problem 3

A triangle has sides of length 7 cm, 4 cm, and 5 cm. How many unique triangles can be drawn that fit that description? Explain or show your reasoning.

Problem 4

A triangle has one side that is 5 units long and an adjacent angle that measures \(25^\circ\). The two other angles in the triangle measure \(90^\circ\) and \(65^\circ\). Complete the two diagrams to create two different triangles with these measurements.

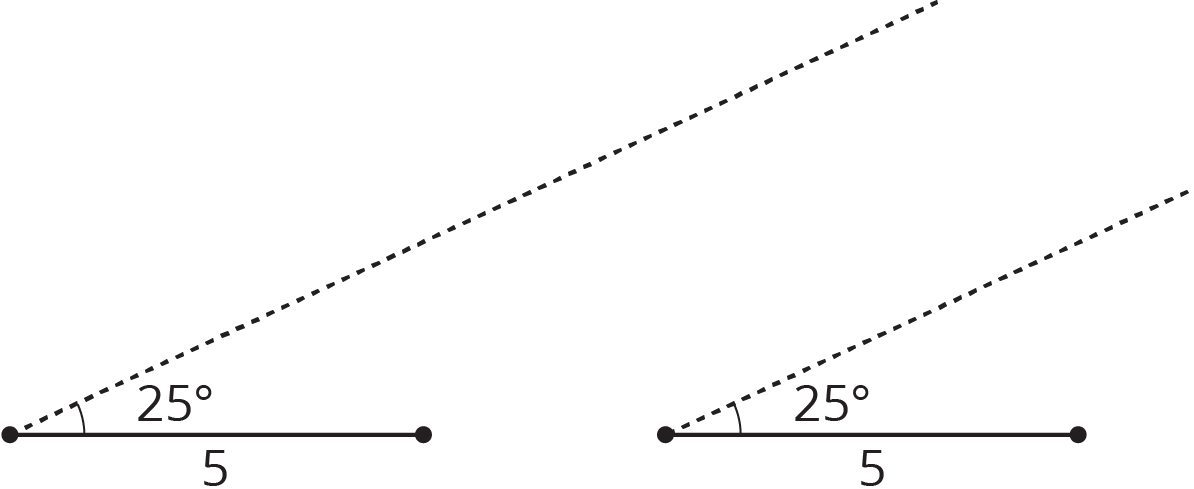
Two images, each a segment with side 5 and a dotted line rising at a 25 degree angle from the segment.

Problem 5

Is it possible to make a triangle that has angles measuring 90 degrees, 30 degrees, and 100 degrees? If so, draw an example. If not, explain your reasoning.