Lesson 16
Triangles with 3 Common Measures
Let’s contrast triangles.
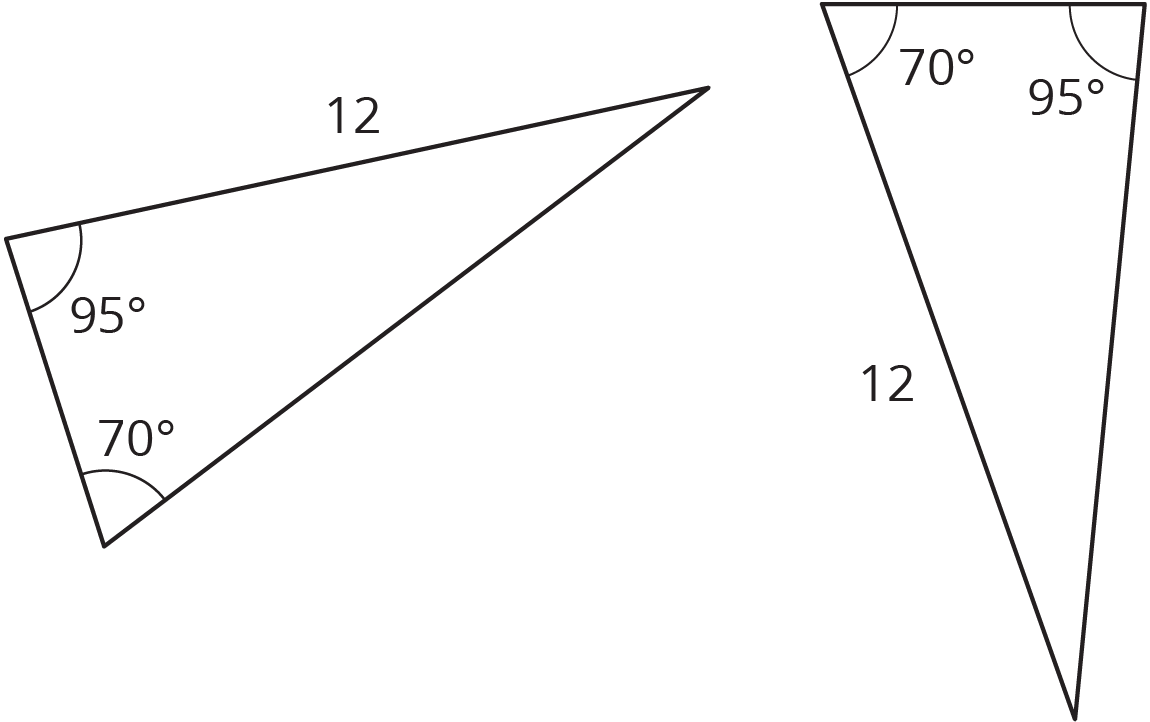
Problem 1
Are these two triangles identical? Explain how you know.
Problem 2
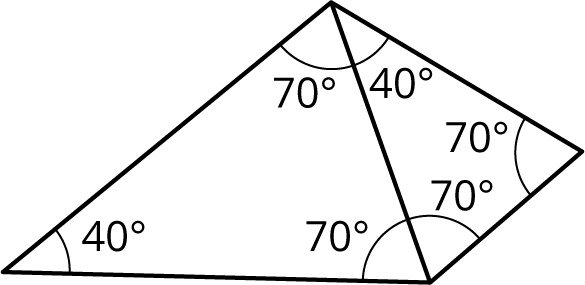
Are these triangles identical? Explain your reasoning.
Problem 3
Tyler claims that if two triangles each have a side length of 11 units and a side length of 8 units, and also an angle measuring \(100^\circ\), they must be identical to each other. Do you agree? Explain your reasoning.
Problem 4
- Draw segment \(PQ\).
- When \(PQ\) is rotated \(180^\circ\) around point \(R\), the resulting segment is the same as \(PQ\). Where could point \(R\) be located?
Problem 5
Here is trapezoid \(ABCD\).
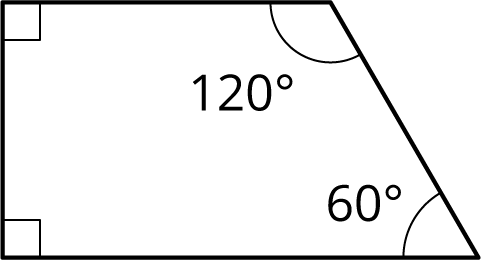
Using rigid transformations on the trapezoid, build a pattern. Describe some of the rigid transformations you used.