Lesson 12

Alternate Interior Angles

Let’s explore why some angles are always equal.

Problem 1

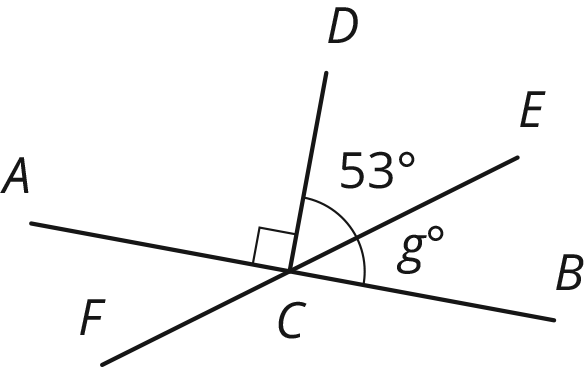
Segments \(AB\), \(EF\), and \(CD\) intersect at point \(C\), and angle \(ACD\) is a right angle. Find the value of \(g\).

Segment A, B, segment E F, and segment C D intersect at point C. Clockwise, the endpoints are A, D, E, B, F. Angle A, C D is a right angle. Angle D C E is 53 degrees, angle E C B is g degrees.

Problem 2

\(M\) is a point on line segment \(KL\). \(NM\) is a line segment. Select all the equations that represent the relationship between the measures of the angles in the figure.

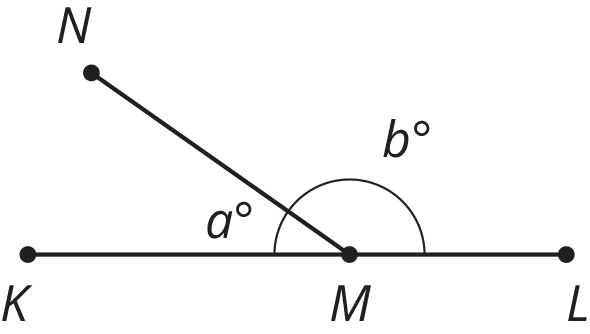
M is a point on line segment K L. Segment N M creates two angles, measure a, degrees and b degrees.
A:

\(a=b\)

B:

\(a+b=90\)

C:

\(b=90-a\)

D:

\(a+b=180\)

E:

\(180-a=b\)

F:

\(180=b-a\)

Problem 3

Use the diagram to find the measure of each angle.

  1. \(m\angle ABC\)
  2. \(m\angle EBD\)
  3. \(m\angle ABE\)
Two lines, line E C and line A D, that intersect at point B. Angle C B D is labeled 45 degrees.
(From Unit 1, Lesson 8.)

Problem 4

Lines \(k\) and \(\ell\) are parallel, and the measure of angle \(ABC\) is 19 degrees.

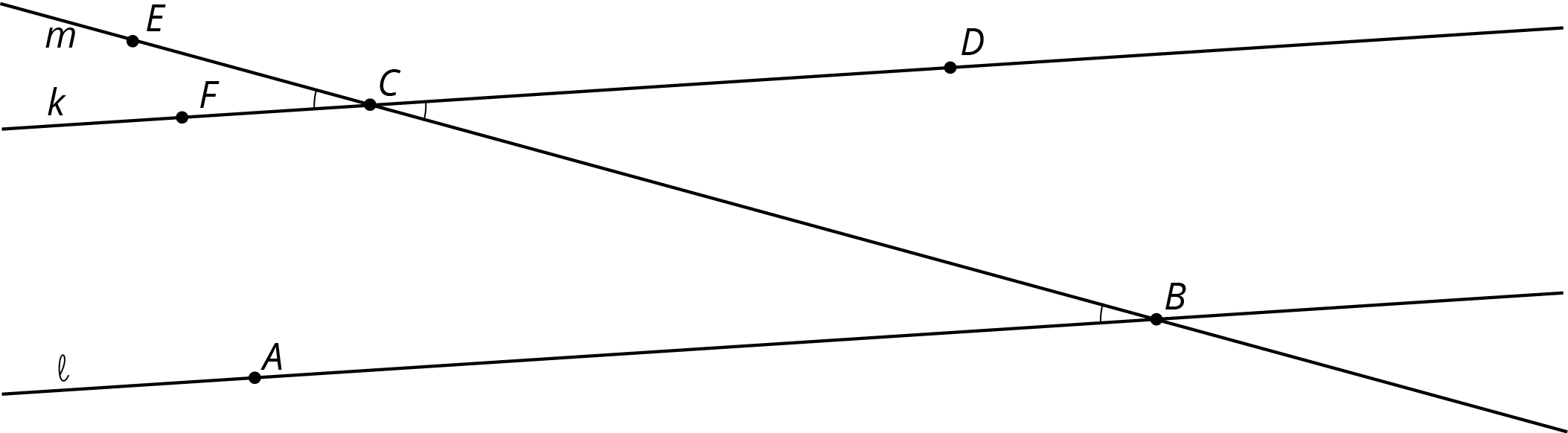
Two parallel lines, k and l, cut by transversal line m.
  1. Explain why the measure of angle \(ECF\) is 19 degrees. If you get stuck, consider translating line \(\ell\) by moving \(B\) to \(C\).
  2. What is the measure of angle \(BCD\)? Explain.

Problem 5

The diagram shows three lines with some marked angle measures.

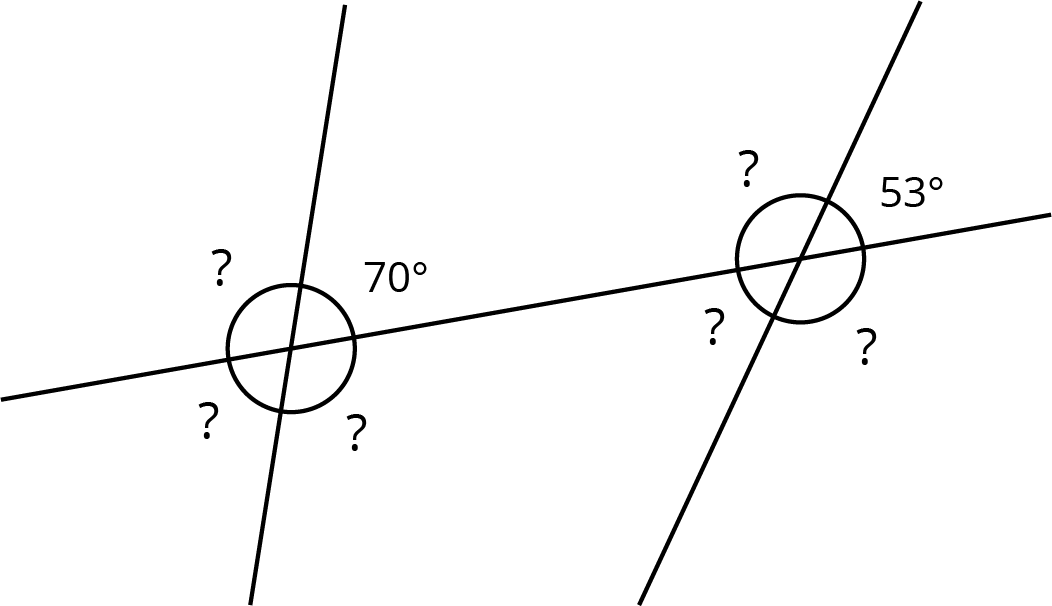
Two lines that do not intersect. A third line intersects with both lines.

Find the missing angle measures marked with question marks.

Problem 6

Lines \(s\) and \(t\) are parallel. Find the value of \(x\).

Four lines. Two parallel lines are labeled s and t. Two other lines that intersect at a right angle at a point on line t. One angle is labeled 40 degrees. Another angle is labeled x degrees.