Lesson 6
Finding Side Lengths of Triangles
Problem 1
Here is a diagram of an acute triangle and three squares.

Priya says the area of the large unmarked square is 26 square units because \(9+17=26\). Do you agree? Explain your reasoning.
Solution
For access, consult one of our IM Certified Partners.
Problem 2
\(m\), \(p\), and \(z\) represent the lengths of the three sides of this right triangle.
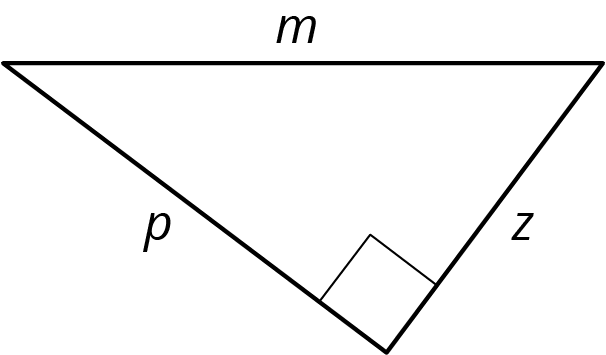
Select all the equations that represent the relationship between \(m\), \(p\), and \(z\).
\(m^2+p^2=z^2\)
\(m^2=p^2+z^2\)
\(m^2=z^2+p^2\)
\(p^2+m^2=z^2\)
\(z^2+p^2=m^2\)
\(p^2+z^2=m^2\)
Solution
For access, consult one of our IM Certified Partners.
Problem 3
The lengths of the three sides are given for several right triangles. For each, write an equation that expresses the relationship between the lengths of the three sides.
- 10, 6, 8
- \(\sqrt5, \sqrt3, \sqrt8\)
- 5, \(\sqrt5, \sqrt{30}\)
- 1, \(\sqrt{37}\), 6
- 3, \(\sqrt{2}, \sqrt7\)
Solution
For access, consult one of our IM Certified Partners.
Problem 4
Order the following expressions from least to greatest.
\(25\div 10\)
\(250,\!000 \div 1,\!000\)
\(2.5 \div 1,\!000\)
\(0.025\div 1\)
Solution
For access, consult one of our IM Certified Partners.
(From Unit 4, Lesson 1.)Problem 5
Which is the best explanation for why \(\text-\sqrt{10}\) is irrational?
\(\text- \sqrt{10}\) is irrational because it is not rational.
\(\text- \sqrt{10}\) is irrational because it is less than zero.
\(\text- \sqrt{10}\) is irrational because it is not a whole number.
\(\text- \sqrt{10}\) is irrational because if I put \(\text- \sqrt{10}\) into a calculator, I get -3.16227766, which does not make a repeating pattern.
Solution
For access, consult one of our IM Certified Partners.
(From Unit 8, Lesson 3.)Problem 6
A teacher tells her students she is just over 1 and \(\frac{1}{2}\) billion seconds old.
- Write her age in seconds using scientific notation.
- What is a more reasonable unit of measurement for this situation?
- How old is she when you use a more reasonable unit of measurement?
Solution
For access, consult one of our IM Certified Partners.
(From Unit 7, Lesson 15.)