Lesson 6
Finding Side Lengths of Triangles
Let’s find triangle side lengths.
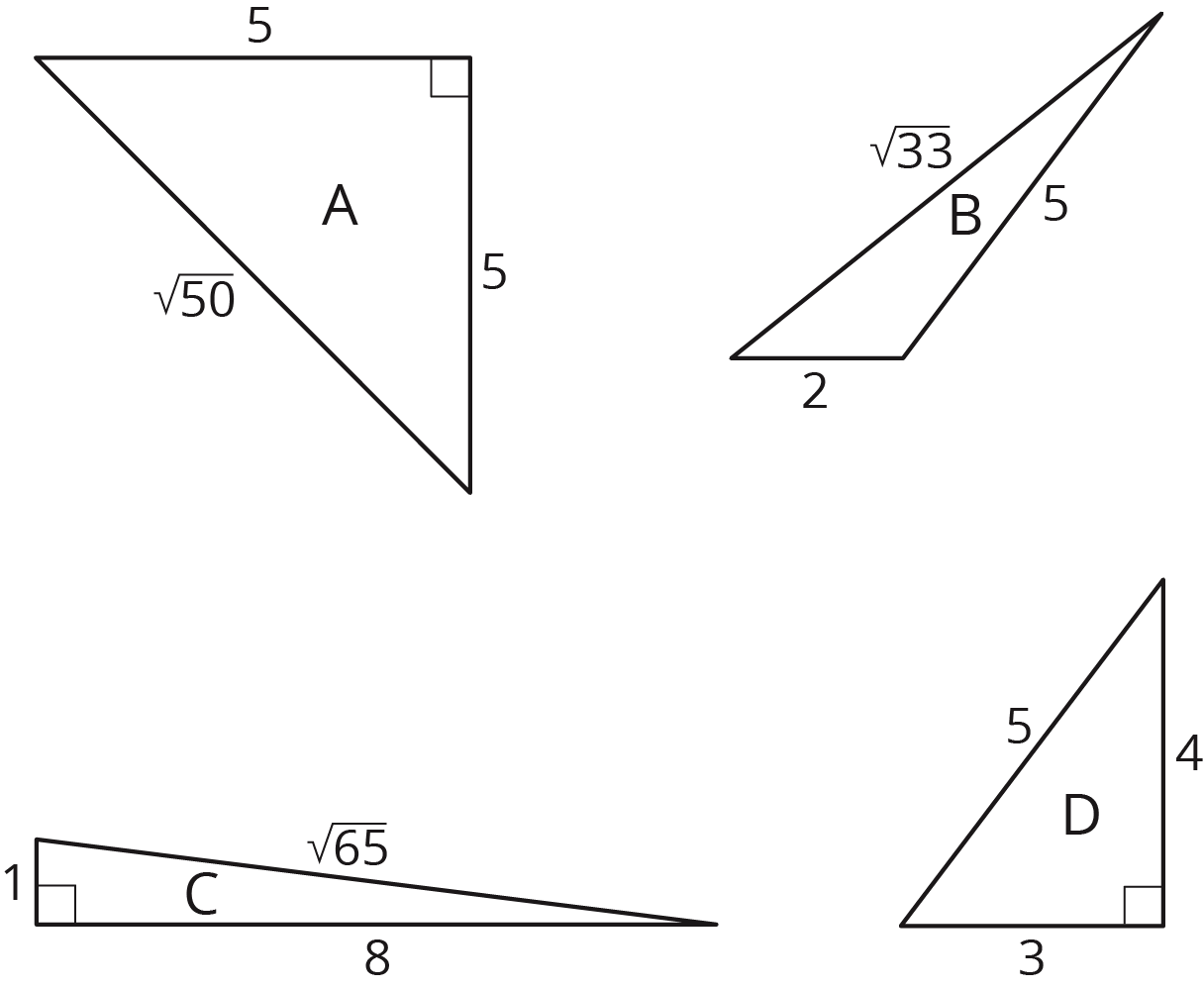
6.1: Which One Doesn’t Belong: Triangles
Which triangle doesn’t belong?
6.2: A Table of Triangles
-
Complete the tables for these three triangles:
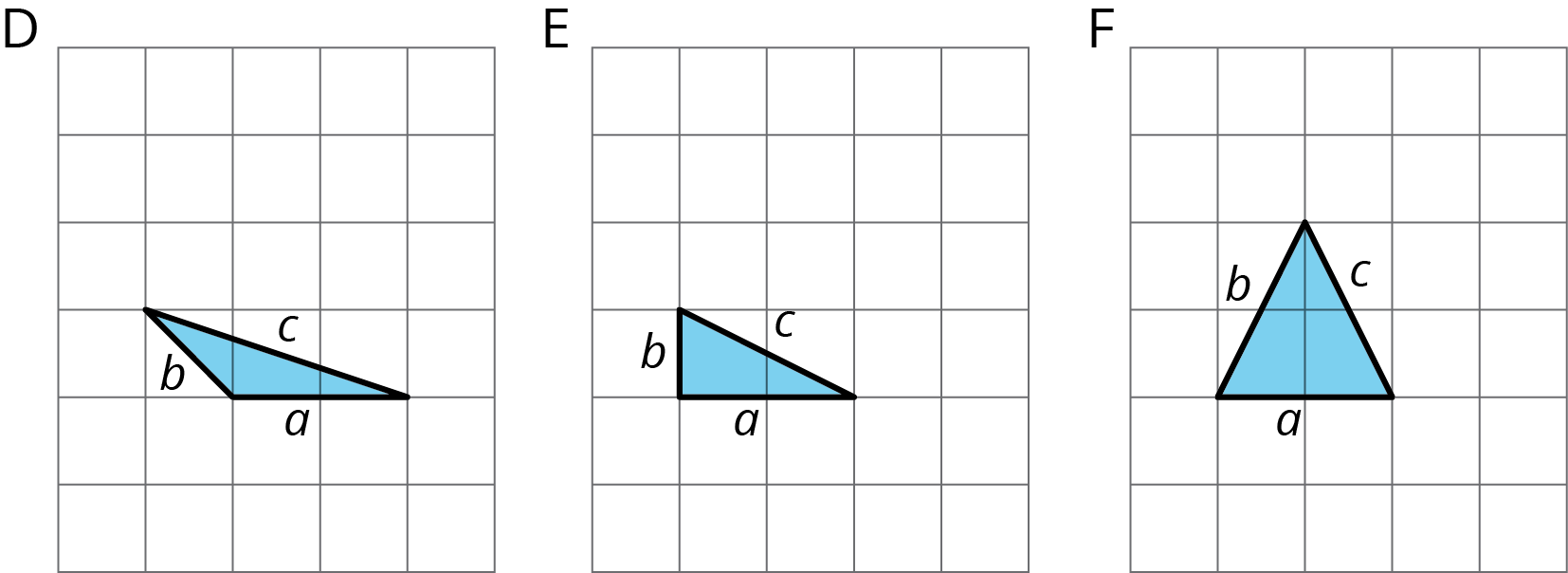
triangle \(a\) \(b\) \(c\) D E F triangle \(a^2\) \(b^2\) \(c^2\) D E F - What do you notice about the values in the table for Triangle E but not for Triangles D and F?
- Complete the tables for these three more triangles:
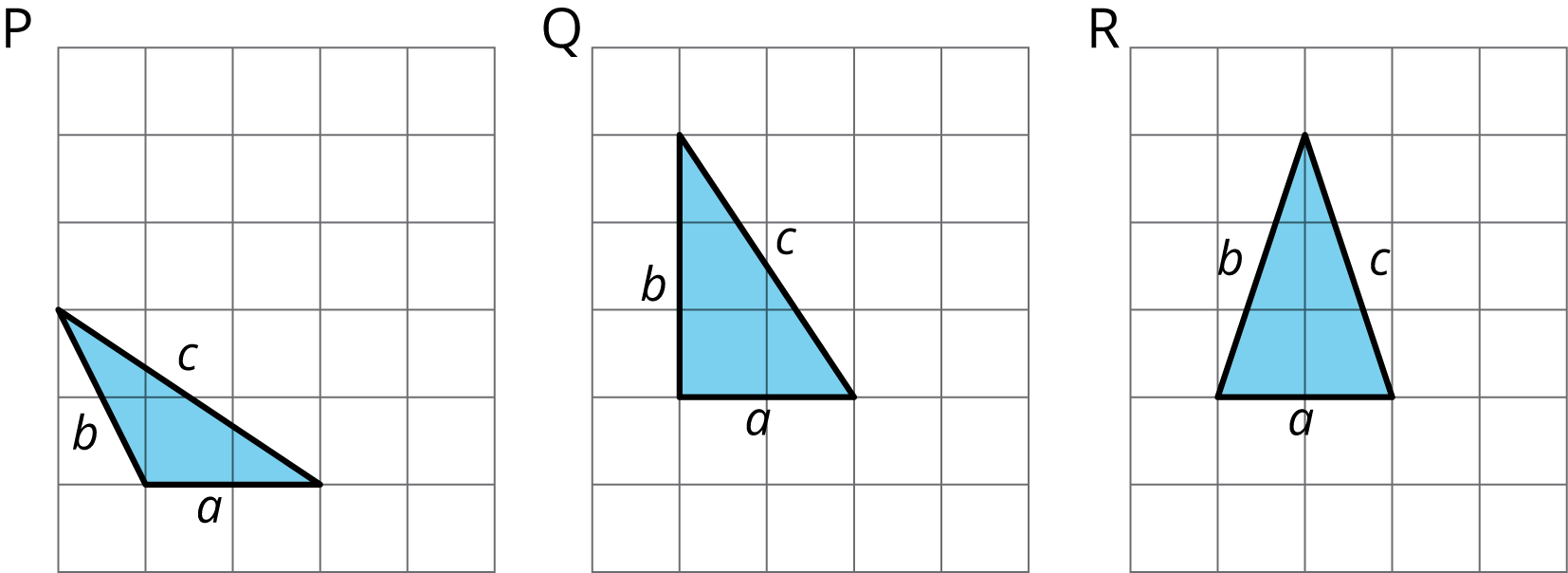
triangle \(a\) \(b\) \(c\) P Q R triangle \(a^2\) \(b^2\) \(c^2\) P Q R - What do you notice about the values in the table for Triangle Q but not for Triangles P and R?
- What do Triangle E and Triangle Q have in common?
6.3: Meet the Pythagorean Theorem
- Find the missing side lengths. Be prepared to explain your reasoning.
- For which triangles does \(a^2+b^2=c^2\)?



If the four shaded triangles in the figure are congruent right triangles, does the inner quadrilateral have to be a square? Explain how you know.

Summary
A right triangle is a triangle with a right angle. In a right triangle, the side opposite the right angle is called the hypotenuse, and the two other sides are called its legs. Here are some right triangles with the hypotenuse and legs labeled:
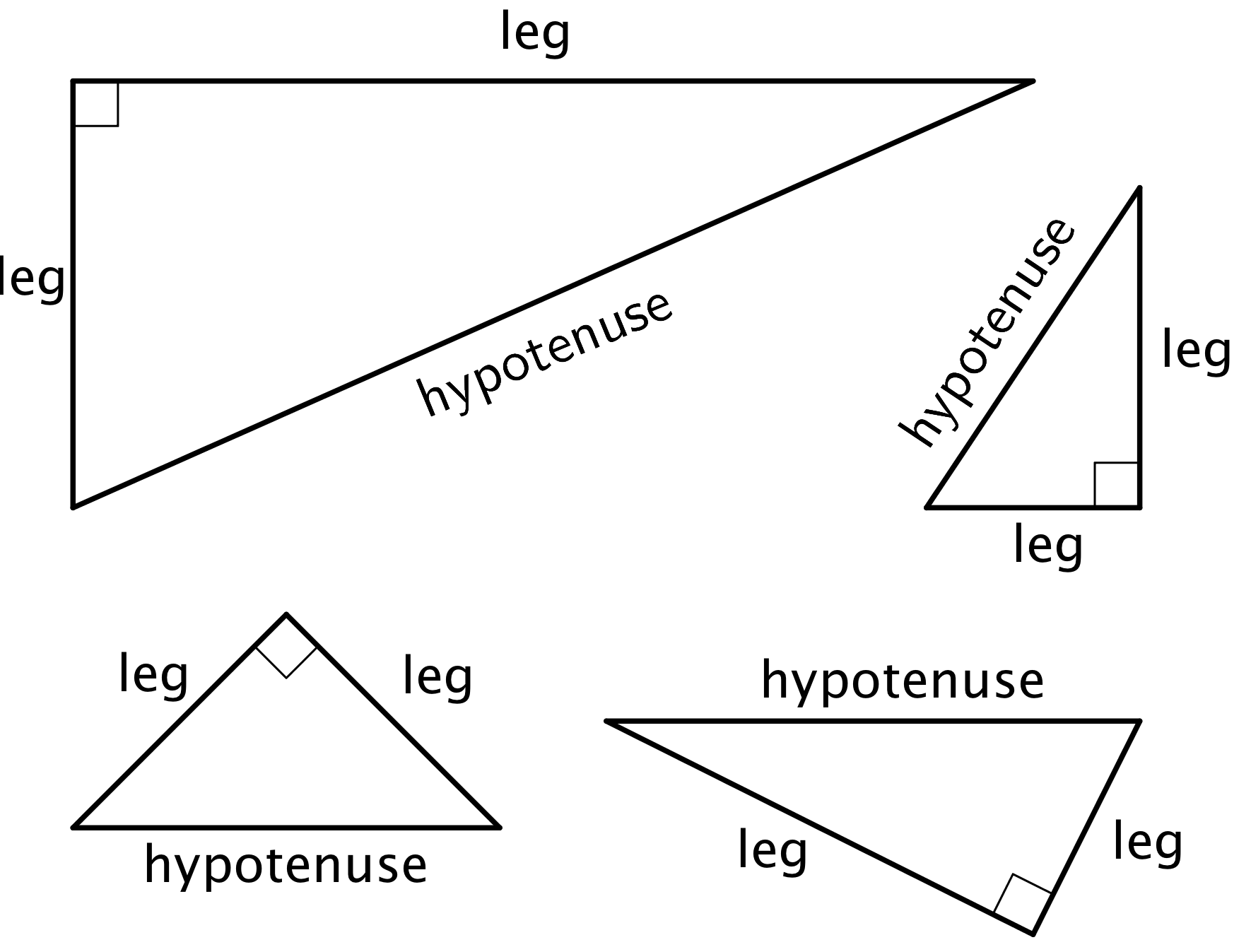
We often use the letters \(a\) and \(b\) to represent the lengths of the shorter sides of a triangle and \(c\) to represent the length of the longest side of a right triangle. If the triangle is a right triangle, then \(a\) and \(b\) are used to represent the lengths of the legs, and \(c\) is used to represent the length of the hypotenuse (since the hypotenuse is always the longest side of a right triangle). For example, in this right triangle, \(a=\sqrt{20}\), \(b=\sqrt5\), and \(c=5\).
Here are some right triangles:

Notice that for these examples of right triangles, the square of the hypotenuse is equal to the sum of the squares of the legs. In the first right triangle in the diagram, \(9+16=25\), in the second, \(1+16=17\), and in the third, \(9+9=18\). Expressed another way, we have \(\displaystyle a^2+b^2=c^2\) This is a property of all right triangles, not just these examples, and is often known as the Pythagorean Theorem. The name comes from a mathematician named Pythagoras who lived in ancient Greece around 2,500 BCE, but this property of right triangles was also discovered independently by mathematicians in other ancient cultures including Babylon, India, and China. In China, a name for the same relationship is the Shang Gao Theorem. In future lessons, you will learn some ways to explain why the Pythagorean Theorem is true for any right triangle.
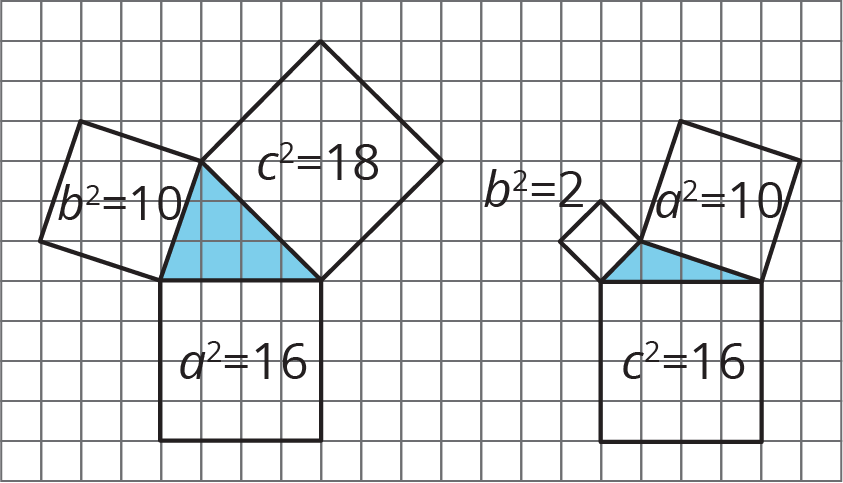
It is important to note that this relationship does not hold for all triangles. Here are some triangles that are not right triangles, and notice that the lengths of their sides do not have the special relationship \(a^2+b^2=c^2\). That is, \(16+10\) does not equal 18, and \(2+10\) does not equal 16.
Glossary Entries
- Pythagorean Theorem
The Pythagorean Theorem describes the relationship between the side lengths of right triangles.
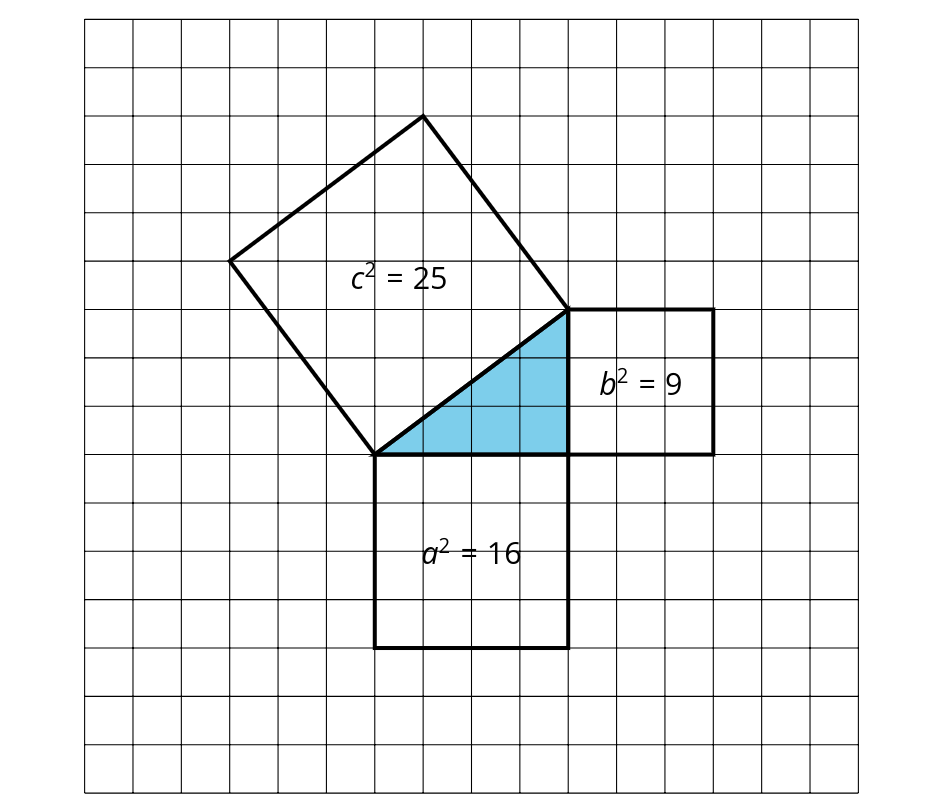
The diagram shows a right triangle with squares built on each side. If we add the areas of the two small squares, we get the area of the larger square.
The square of the hypotenuse is equal to the sum of the squares of the legs. This is written as \(a^2+b^2=c^2\).
- hypotenuse
The hypotenuse is the side of a right triangle that is opposite the right angle. It is the longest side of a right triangle.
Here are some right triangles. Each hypotenuse is labeled.

- legs
The legs of a right triangle are the sides that make the right angle.
Here are some right triangles. Each leg is labeled.
