Lesson 2
Changing Temperatures
2.1: Which One Doesn’t Belong: Arrows (5 minutes)
Warm-up
In this warm-up, students compare four number line diagrams with arrows. To give all students access the activity, each diagram has one obvious reason it does not belong. Students will use diagrams like these later in the lesson to represent sums of signed numbers, but for this activity, the goal is to just get them used to analyzing these types of diagrams carefully before they have to interpret them in terms of rational number arithmetic.
Launch
Arrange students in groups of 2–4. Display the image of the four figures for all to see. Ask students to indicate when they have noticed one figure that does not belong and can explain why. Give students 1 minute of quiet think time and then time to share their thinking with their group. After everyone has conferred in groups, ask the group to offer at least one reason each figure doesn’t belong.
Student Facing
Which pair of arrows doesn't belong?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
After students have conferred in groups, invite each group to share one reason why a particular figure might not belong. Record and display the responses for all to see. After each response, poll the rest of the class if they agree or disagree. Since there is no single correct answer to the question of which diagram does not belong, attend to students’ explanations and ensure the reasons given make sense.
Ask the students what they think the arrows might represent. After collecting responses, say we are going to represent positive and negative numbers and their sums using arrows on a number line.
2.2: Warmer and Colder (15 minutes)
Activity
In this activity, the context of temperature is used to help students make sense of adding signed numbers (MP2). First students reason about temperature increases and decreases. They represent these increases and decreases on a number line, and then connect these temperature changes with adding positive numbers for increases and adding negative numbers for decreases. Students repeatedly add numbers to 40 and then to -20 to see that adding a positive number is the same as moving to the right on the number line and adding a negative number is the same as moving to the left on the number line (MP8).
Launch
Arrange students in groups of 2. Ask them, “If the temperature starts at 40 degrees and increases 10 degrees, what will the final temperature be?” Show them this number line:

Explain how the diagram represents the situation, including the start temperature, the change, and the final temperature. Point out that in the table, this situation is represented by an equation where the initial temperature and change in temperature are added together to find the final temperature.
Next, ask students to think about the change in the second row of the table. Give students 1 minute of quiet work time to draw the diagram that shows a decrease of 5 degrees and to think about how they can represent this with an addition equation. Have them discuss with a partner for 1 minute. Ask a few students to share what they think the addition equation should be. Be sure students agree on the correct addition equation before moving on. Tell students they will be answering similar questions,
- first by reasoning through the temperature change using whatever method makes sense,
- then drawing a diagram to show the temperature change, and
- finally, by writing an equation to represent the situation.
Give students 4 minutes of quiet work time followed by partner and then whole group discussion.
Supports accessibility for: Visual-spatial processing
Design Principle(s): Support sense-making; Maximize meta-awareness
Student Facing
-
Complete the table and draw a number line diagram for each situation.
start (\(^\circ\text{C}\)) change (\(^\circ\text{C}\)) final (\(^\circ \text{C}\)) addition equation a +40 10 degrees warmer +50 \(40 + 10 = 50\) b +40 5 degrees colder c +40 30 degrees colder d +40 40 degrees colder e +40 50 degrees colder -
-
Complete the table and draw a number line diagram for each situation.
start (\(^\circ\text{C}\)) change (\(^\circ\text{C}\)) final (\(^\circ\text{C}\)) addition equation a -20 30 degrees warmer b -20 35 degrees warmer c -20 15 degrees warmer d -20 15 degrees colder -
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
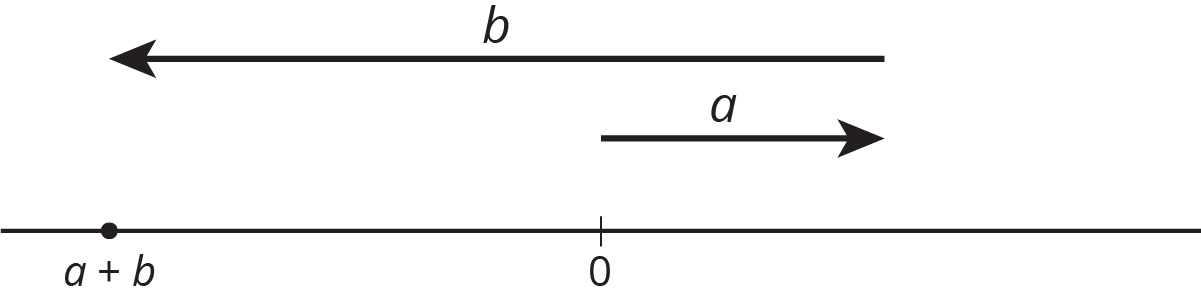
For the numbers \(a\) and \(b\) represented in the figure, which expression is equal to \(|a+b|\)?
\(|a|+|b|\)
\(|a|-|b|\)
\(|b|-|a|\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students,
- “How can we represent an increase in temperature on a number line?” (An arrow pointing to the right.)
- “How can we represent a decrease in temperature on a number line?” (An arrow pointing to the left.)
- “How are positive numbers represented on a number line?” (Arrows pointing to the right.)
- “How are negative numbers represented on a number line?” (Arrows pointing to the left.)
- “How can we represent a sum of two numbers?” (But the arrows so the tail of the second is at the tip of the first.)
- “How can we determine the sum from the diagram?” (It is at the tip of the second arrow.)
- “What happens when we add a positive number to another number?” (We move to the right on the number line.)
- “What happens when we add a negative number to another number?” (We move to the left on the number line.)
2.3: Winter Temperatures (10 minutes)
Activity
In this activity, students use what they learned in the previous activity to find temperature differences and connect them to addition equations. Students who use number line diagrams are using tools strategically (MP5). Students may draw number line diagrams in a variety of ways; what matters is that they can explain how their diagrams represent the situation. Students may think of these questions in terms of subtraction; that is completely correct, but the discussion should focus on how to think of these situations in terms of addition. Students will have an opportunity to connect addition and subtraction in a future lesson.
Launch
Before students start working, it may be helpful to display a map of the United States and point out the locations of the cities in the problem. Explain that in the northern hemisphere, it tends to be colder the farther north you are.
If students are using the digital version, ask them to think about and respond to the questions before testing out their conclusions with the embedded applet. If students jump right to using the applet, they might skip some deep thinking that results from figuring out how to represent the initial temperature, change in temperature, and final temperature, as well as miss out on practice representing these operations with a number line.
Design Principle(s): Support sense-making
Student Facing
One winter day, the temperature in Houston is \(8^\circ\) Celsius. Find the temperatures in these other cities. Explain or show your reasoning.
- In Orlando, it is \(10^\circ\) warmer than it is in Houston.
- In Salt Lake City, it is \(8^\circ\) colder than it is in Houston.
- In Minneapolis, it is \(20^\circ\) colder than it is in Houston.
- In Fairbanks, it is \(10^\circ\) colder than it is in Minneapolis.
- Use the thermometer applet to verify your answers and explore your own scenarios.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Before students start working, it may be helpful to display a map of the United States and point out the locations of the cities in the problem. Explain that in the northern hemisphere, it tends to be colder the farther north you are.
If students are using the digital version, ask them to think about and respond to the questions before testing out their conclusions with the embedded applet. If students jump right to using the applet, they might skip some deep thinking that results from figuring out how to represent the initial temperature, change in temperature, and final temperature, as well as miss out on practice representing these operations with a number line.
Design Principle(s): Support sense-making
Student Facing
One winter day, the temperature in Houston is \(8^\circ\) Celsius. Find the temperatures in these other cities. Explain or show your reasoning.
-
In Orlando, it is \(10^\circ\) warmer than it is in Houston.
-
In Salt Lake City, it is \(8^\circ\) colder than it is in Houston.
-
In Minneapolis, it is \(20^\circ\) colder than it is in Houston.
-
In Fairbanks, it is \(10^\circ\) colder than it is in Minneapolis.
- Write an addition equation that represents the relationship between the temperature in Houston and the temperature in Fairbanks.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students struggle to find the temperature in Minneapolis, thinking that \(8 - 20\) doesn't have an answer, suggest they represent the decrease in temperature as \(8 + (\text-20)\) and use a number line to reason about the resulting temperature.
Activity Synthesis
Ask students who used number lines to share their reasoning. If a students correctly describes the situation in terms of subtraction, acknowledge that perspective and then ask them if they can also think of it in terms of addition. If no students used a number line, demonstrate how to represent these situations a number line diagram. For example, we can draw this diagram for Minneapolis:

The initial temperature of 8 is represented by an arrow starting at 0 and going 8 units to the right. The decrease in temperature is represented by an arrow starting at 8 and going 20 units to the left. The final temperature is represented by a point at -12, where the second arrow ends. Remind them that we can represent this with an addition equation: \(\displaystyle 8 + (\text-20) = \text-12\)
Lesson Synthesis
Lesson Synthesis
Main learning points:
- We can represent a decrease as adding a negative number.
- We can represent addition on a number line with two arrows, the second arrow starting where the first arrow ends.
- We can represent a negative addend on a number line as an arrow pointing to the left.
Discussion questions:
- “How can you represent an increase or decrease in temperature using an addition equation?”
- “How can you represent an addition equation on a number line?”
2.4: Cool-down - Stories about Temperature (10 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
If it is \(42^\circ\) outside and the temperature increases by \(7^\circ\), then we can add the initial temperature and the change in temperature to find the final temperature.
\(42 + 7 = 49\)
If the temperature decreases by \(7^\circ\), we can either subtract \(42-7\) to find the final temperature, or we can think of the change as \(\text-7^\circ\). Again, we can add to find the final temperature.
\(42 + (\text-7) = 35\)
In general, we can represent a change in temperature with a positive number if it increases and a negative number if it decreases. Then we can find the final temperature by adding the initial temperature and the change. If it is \(3^\circ\) and the temperature decreases by \(7^\circ\), then we can add to find the final temperature.
\(3+ (\text-7) = \text-4\)
We can represent signed numbers with arrows on a number line. We can represent positive numbers with arrows that start at 0 and point to the right. For example, this arrow represents +10 because it is 10 units long and it points to the right.

We can represent negative numbers with arrows that start at 0 and point to the left. For example, this arrow represents -4 because it is 4 units long and it points to the left.
To represent addition, we put the arrows “tip to tail.” So this diagram represents \(3+5\):

And this represents \(3 + (\text-5)\):