Lesson 9
Multiplying Rational Numbers
9.1: Before and After (5 minutes)
Warm-up
In this lesson, students will interpret negative time in context. The warm-up primes them for those interpretations.
Launch
Arrange students in groups of 2. Give students 30 seconds of quiet think time, followed by partner discussion.
Student Facing

Where was the girl:
- 5 seconds after this picture was taken? Mark her approximate location on the picture.
- 5 seconds before this picture was taken? Mark her approximate location on the picture.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to come to agreement with their partners, and help them to productively resolve any discrepancies. Point out that if she is walking at a constant speed, then her positions before and after will be equally far from her position in the picture.
9.2: Backwards in Time (15 minutes)
Activity
Students use their earlier understanding of a chosen zero point and description of positive and negative velocity, and extend this to include negative values for time to represent a time before the time assigned chosen as zero. This will produce different end points depending on if the velocity or time is negative or positive. Students use the context to help make sense of the arithmetic problems (MP2). Looking at a number of different examples will help students describe rules for identifying the sign of the product of two negative numbers (MP8). Students may choose to use a number line to help them in their reasoning; this is an example of using appropriate tools strategically (MP5).
Launch
Keep students in the same groups. Remind the students of movement east or west as positive or negative velocity.
This activity is the same context as one in the previous lesson, and the questions are related. So students should be able to get to work rather quickly. However, each question requires some careful thought, and one question builds on the other. Consider suggesting that students check in with their partner frequently and explain their thinking. Additionally, you might consider asking students to pause after each question for a quick whole-class discussion before continuing to the next question.
Supports accessibility for: Organization; Attention
Design Principle(s): Cultivate conversation; Support sense-making
Student Facing
A traffic safety engineer was studying travel patterns along a highway. She set up a camera and recorded the speed and direction of cars and trucks that passed by the camera. Positions to the east of the camera are positive, and to the west are negative.
-
Here are some positions and times for one car:
position (feet) -180 -120 -60 0 60 120 time (seconds) -3 -2 -1 0 1 2 - In what direction is this car traveling?
- What is its velocity?
-
-
What does it mean when the time is zero?
-
What could it mean to have a negative time?
-
-
Here are the positions and times for a different car whose velocity is -50 feet per second:
position (feet) 0 -50 -100 time (seconds) -3 -2 -1 0 1 2 - Complete the table with the rest of the positions.
- In what direction is this car traveling? Explain how you know.
-
Complete the table for several different cars passing the camera.
velocity
(meters per
second)time after passing
the camera
(seconds)ending
position
(meters)equation car C +25 +10 +250 \(25\boldcdot 10 = 250\) car D -20 +30 car E +32 -40 car F -35 -20 car G -15 -8 -
- If a car is traveling east when it passes the camera, will its position be positive or negative 60 seconds before it passes the camera?
-
If we multiply a positive number and a negative number, is the result positive or negative?
-
- If a car is traveling west when it passes the camera, will its position be positive or negative 60 seconds before it passes the camera?
- If we multiply two negative numbers, is the result positive or negative?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students struggle to calculate the velocity, ask them how fast is the car going after 1 second.
Activity Synthesis
The key thing for students to understand here is that a negative multiplied by another negative is a positive. The last two rows in the table and the final two questions are the keys to this so draw attention to the logical progression that movement in the negative direction will have a positive position when time is negative.
9.3: Cruising (15 minutes)
Optional activity
This is the first of two optional activities. The teacher may choose to implement either of the optional activities that would best reinforce the learning goals for their students.
In this optional activity, students find the position of a car traveling at a constant velocity at different positive and negative times, and plot the points in the coordinate plane. They see that just as with constant speed, the graph goes through \((0,0)\), but because the velocity is negative it slants downward from left to right instead of passing through the first quadrant.
Launch
Arrange students in groups of 2. Give them 4 minutes of quiet work time, followed by partner and then whole-class discussion.
Design Principle(s): Support sense-making
Student Facing
Around noon, a car was traveling -32 meters per second down a highway. At exactly noon (when time was 0), the position of the car was 0 meters.
-
Complete the table.
time (s) -10 -7 -4 -1 2 5 8 11 position (m) - Graph the relationship between the time and the car's position.
- What was the position of the car at -3 seconds?
- What was the position of the car at 6.5 seconds?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 2. Give them 4 minutes of quiet work time, followed by partner and then whole-class discussion.
Design Principle(s): Support sense-making
Student Facing
Around noon, a car was traveling -32 meters per second down a highway. At exactly noon (when time was 0), the position of the car was 0 meters.
-
Complete the table.
time (s) -10 -7 -4 -1 2 5 8 11 position (m) - Graph the relationship between the time and the car's position.

- What was the position of the car at -3 seconds?
- What was the position of the car at 6.5 seconds?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Find the value of these expressions without using a calculator.
\((\text-1)^2\)
\((\text-1)^3\)
\((\text-1)^4\)
\((\text-1)^{99}\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students how the graph is similar and different from the graph of a proportional relationship. Poll the class for the last two questions. Ask students if they can see an equation that relates the time and the position of the car. Record their ideas and make sure everyone comes to agreement that if \(d\) is the position and \(t\) is the time, then \(d = \text-32t\).
9.4: Rational Numbers Multiplication Grid (10 minutes)
Optional activity
In this optional activity, students revisit the representation of a multiplication chart, which may be familiar from previous grades; however, in this activity, the multiplication chart is extended to include negative numbers. Students identify and continue patterns (MP8) to complete the chart and see that it fits the patterns in the chart for the product of two negative numbers to be a positive number.
The blackline master has a multiplication chart that also includes the factors 1.5, -1.5, 3.2, and -3.2, so that students can see how the patterns extend to rational numbers that are not integers. Encourage students to complete the rows and columns for the integers first and then come back to 1.5, -1.5, 3.2, and -3.2 later. Directions are included on the blackline master for a way that students can fold their papers to hide the non-integers while they fill in the integers. If you want students to do this, it would be good to demonstrate and walk them through the process of folding their paper.
Launch
Arrange students in groups of 3. If desired, distribute 1 copy of the blackline master to every student and instruct students to ignore the chart printed in their books or devices. (Also if desired, instruct students to fold their papers according to the directions on the top and right sides of the chart, so that the decimal rows and columns are temporarily hidden.) Give students 30 seconds of quiet think time. Have them share what patterns they notice about the numbers that are already filled in. Give the groups 5 minutes of work time followed by whole-class discussion.
If students have access to the digital materials, students can use the applet to complete the chart. The applet helps students focus on fewer of the numbers and patterns at a time, similar to the purpose of folding the blackline master. Also, the applet gives students immediate feedback on whether their answers are correct which helps them test their theories about ramifications of multiplying by a negative number.
Supports accessibility for: Memory; Conceptual processing
Student Facing
Look at the patterns along the rows and columns and continue those patterns to complete the table. When you have filled in all the boxes you can see, click on the "More Boxes" button.
What does this tell you about multiplication by a negative?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 3. If desired, distribute 1 copy of the blackline master to every student and instruct students to ignore the chart printed in their books or devices. (Also if desired, instruct students to fold their papers according to the directions on the top and right sides of the chart, so that the decimal rows and columns are temporarily hidden.) Give students 30 seconds of quiet think time. Have them share what patterns they notice about the numbers that are already filled in. Give the groups 5 minutes of work time followed by whole-class discussion.
If students have access to the digital materials, students can use the applet to complete the chart. The applet helps students focus on fewer of the numbers and patterns at a time, similar to the purpose of folding the blackline master. Also, the applet gives students immediate feedback on whether their answers are correct which helps them test their theories about ramifications of multiplying by a negative number.
Supports accessibility for: Memory; Conceptual processing
Student Facing
- Complete the shaded boxes in the multiplication square.
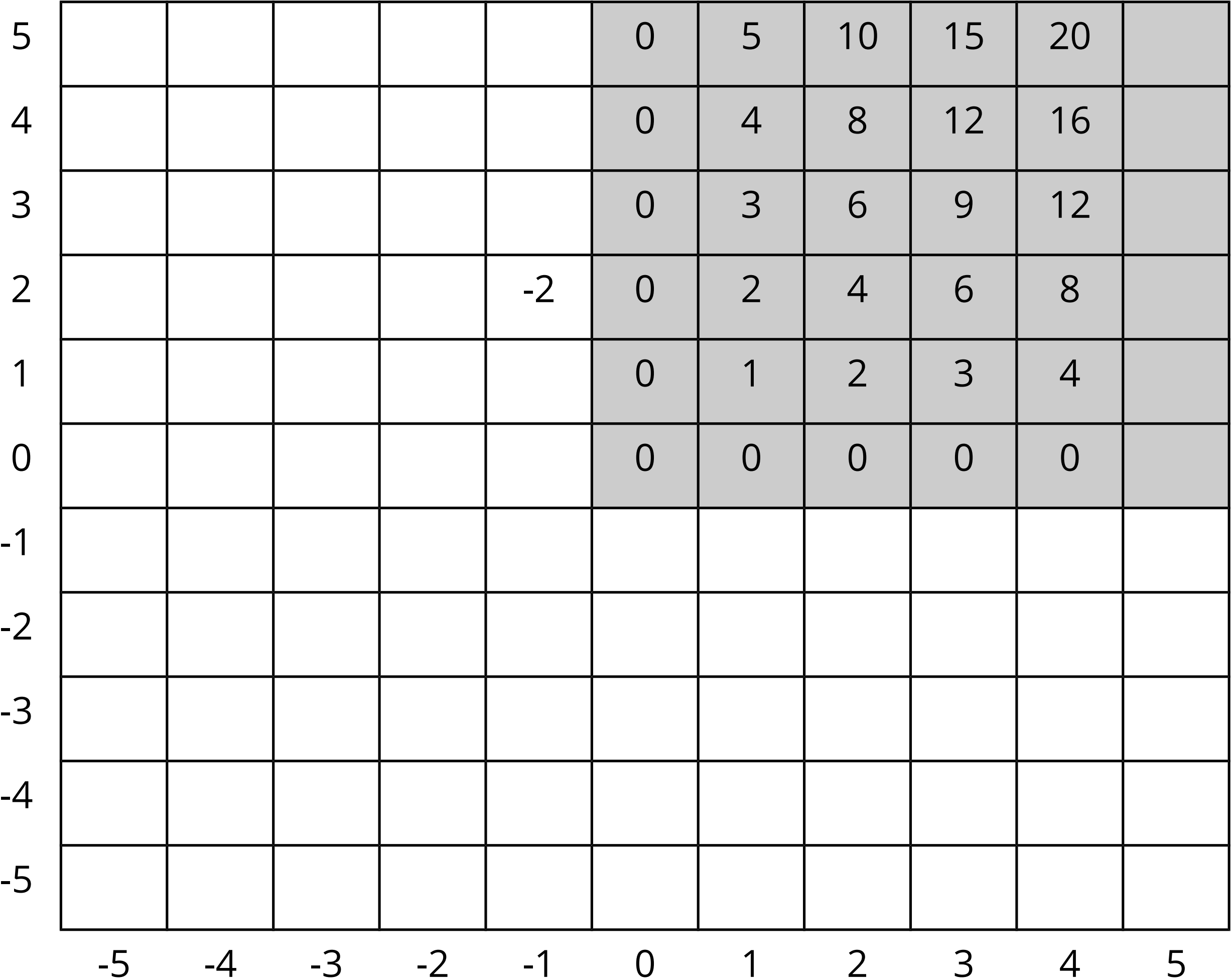
- Look at the patterns along the rows and columns. Continue those patterns into the unshaded boxes.
- Complete the whole table.
- What does this tell you about multiplication with negative numbers?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may need a reminder of how a mutliplication chart works: the factors are listed at the end of the rows and columns, and their products go in the boxes.
Activity Synthesis
The most important takeaway is that it makes sense for the product of two negative numbers to be a positive number, whether or not the numbers are integers. This fits in with the patterns in the extended multiplication chart. Those patterns depend on the distributive property. For example, the reason the numbers in the top row go up by 5s is that \(5(n+1) = 5n + 5\). So when students extend the pattern to negative numbers, they are extending the distributive property.
Display a complete chart for all to see, and ask students to explain the ways in which the chart shows that the product of a negative and a negative is a positive. The general argument involves assuming that a pattern observed in a row or column will continue on the other side of 0.

Lesson Synthesis
Lesson Synthesis
Key takeaways:
- Positive times are after a chosen zero time, and negative times are times before the chosen zero time.
- A positive times a positive is always positive.
- A negative times a positive or a positive times a negative is always negative.
- A negative times a negative is always positive.
Discussion questions:
- How can we represent a time that came before a specific zero point?
- What kind of number do you get when you multiply a negative number by a positive number? Use a context from the lesson to explain why this makes sense.
- What kind of number do you get when you multiply a negative number by a negative number? Use a context from the lesson to explain why this makes sense.
9.5: Cool-down - True Statements (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
We can use signed numbers to represent time relative to a chosen point in time. We can think of this as starting a stopwatch. The positive times are after the watch starts, and negative times are times before the watch starts.
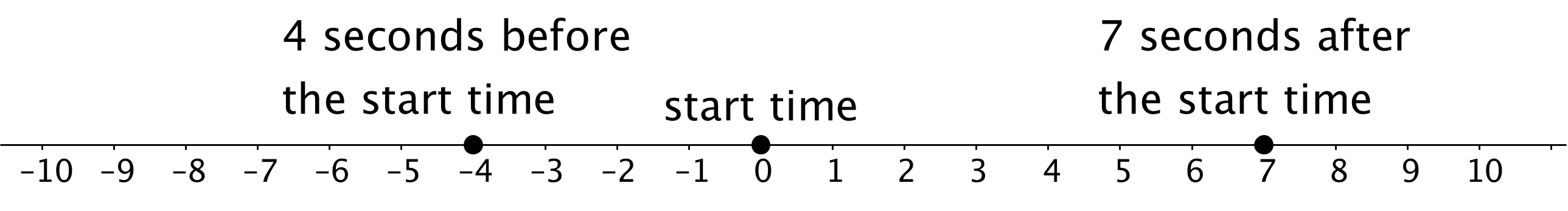
If a car is at position 0 and is moving in a positive direction, then for times after that (positive times), it will have a positive position. A positive times a positive is positive.

If a car is at position 0 and is moving in a negative direction, then for times after that (positive times), it will have a negative position. A negative times a positive is negative.

If a car is at position 0 and is moving in a positive direction, then for times before that (negative times), it must have had a negative position. A positive times a negative is negative.

If a car is at position 0 and is moving in a negative direction, then for times before that (negative times), it must have had a positive position. A negative times a negative is positive.

Here is another way of seeing this:
We can think of \(3\boldcdot 5\) as \(5 + 5 + 5\), which has a value of 15.
We can think of \(3\boldcdot (\text-5)\) as \(\text-5 + \text-5 + \text-5\), which has a value of -15.
We know we can multiply positive numbers in any order: \(3\boldcdot 5=5\boldcdot 3\)
If we can multiply signed numbers in any order, then \((\text-5)\boldcdot 3\) would also equal -15.
Now let’s think about multiplying two negatives.
We can find \(\text-5\boldcdot (3+\text-3)\) in two ways:
- Applying the distributive property:
\(\text-5\boldcdot 3 + \text-5\boldcdot (\text-3)\)
- Adding the numbers in parentheses:
\(\text-5\boldcdot (0) = 0\)
This means that these expressions must be equal.
\(\text-5\boldcdot 3 + \text-5\boldcdot (\text-3) = 0\)
Multiplying the first two numbers gives
\(\text-15 + \text-5\boldcdot (\text-3) = 0\)
Which means that
\( \text-5\boldcdot (\text-3) = 15\)
There was nothing special about these particular numbers. This always works!
- A positive times a positive is always positive.
- A negative times a positive or a positive times a negative is always negative.
- A negative times a negative is always positive.