Lesson 13
Expressions with Rational Numbers
Problem 1
The value of \(x\) is \(\frac {\text{-}1}{4}\). Order these expressions from least to greatest:
\(x\)
\(1-x\)
\(x-1\)
\(\text-1\div x\)
Solution
For access, consult one of our IM Certified Partners.
Problem 2
Here are four expressions that have the value \(\frac {\text{-}1}{2}\):
\(\frac {\text{-}1}{4} + \left(\frac {\text{-}1}{4}\right)\)
\(\frac12 - 1\)
\(\text-2 \boldcdot \frac14\)
\(\text-1 \div 2\)
Write five expressions: a sum, a difference, a product, a quotient, and one that involves at least two operations that have the value \(\frac {\text{-}3}{4}\).
Solution
For access, consult one of our IM Certified Partners.
Problem 3
Find the value of each expression.
- \(\text-22 + 5\)
- \(\text-22 -(\text-5)\)
- \((\text-22) (\text-5)\)
- \(\text-22 \div 5\)
Solution
For access, consult one of our IM Certified Partners.
Problem 4
The price of an ice cream cone is $3.25, but it costs $3.51 with tax. What is the sales tax rate?
Solution
For access, consult one of our IM Certified Partners.
(From Unit 4, Lesson 10.)Problem 5
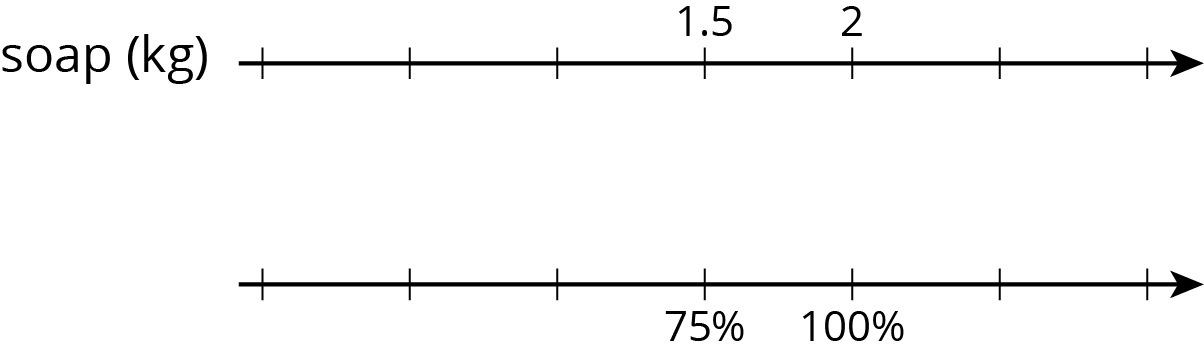
Two students are both working on the same problem: A box of laundry soap has 25% more soap in its new box. The new box holds 2 kg. How much soap did the old box hold?
- Here is how Jada set up her double number line.
- Here is how Lin set up her double number line.
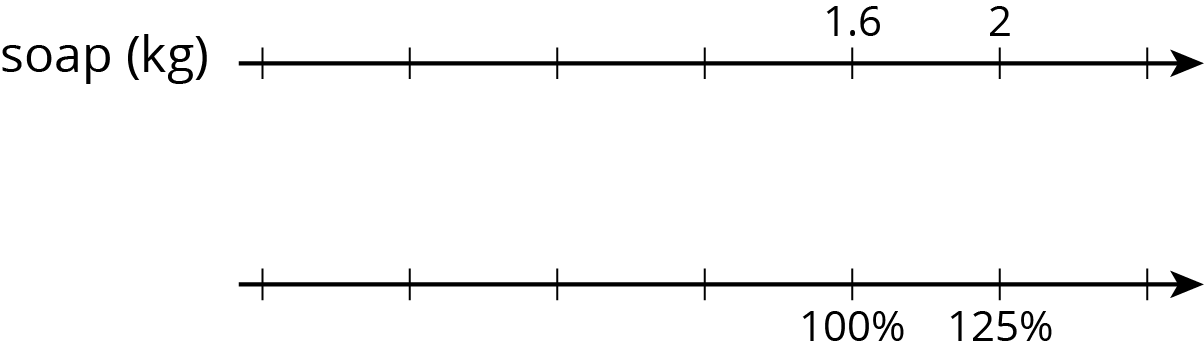
Do you agree with either of them? Explain or show your reasoning.
Solution
For access, consult one of our IM Certified Partners.
(From Unit 4, Lesson 7.)Problem 6
- A coffee maker’s directions say to use 2 tablespoons of ground coffee for every 6 ounces of water. How much coffee should you use for 33 ounces of water?
- A runner is running a 10 km race. It takes her 17.5 minutes to reach the 2.5 km mark. At that rate, how long will it take her to run the whole race?
Solution
For access, consult one of our IM Certified Partners.
(From Unit 4, Lesson 3.)