Lesson 7
A Proof of the Pythagorean Theorem
Let’s prove the Pythagorean Theorem.
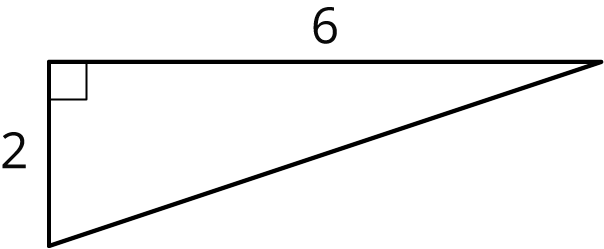
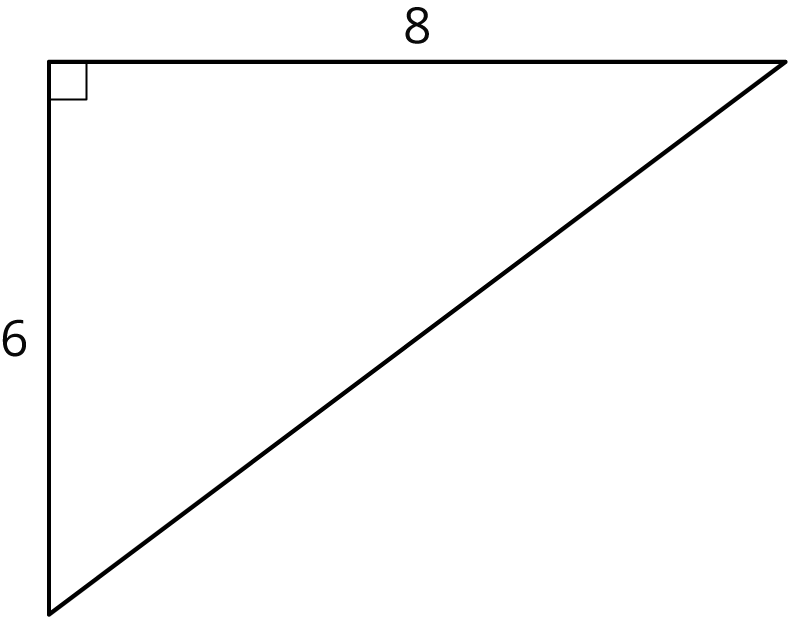
Problem 1
- Find the lengths of the unlabeled sides.
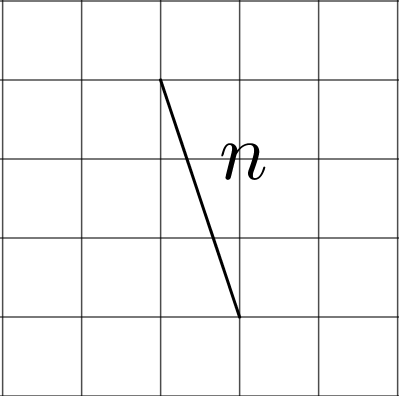
- One segment is \(n\) units long and the other is \(p\) units long. Find the value of \(n\) and \(p\). (Each small grid square is 1 square unit.)

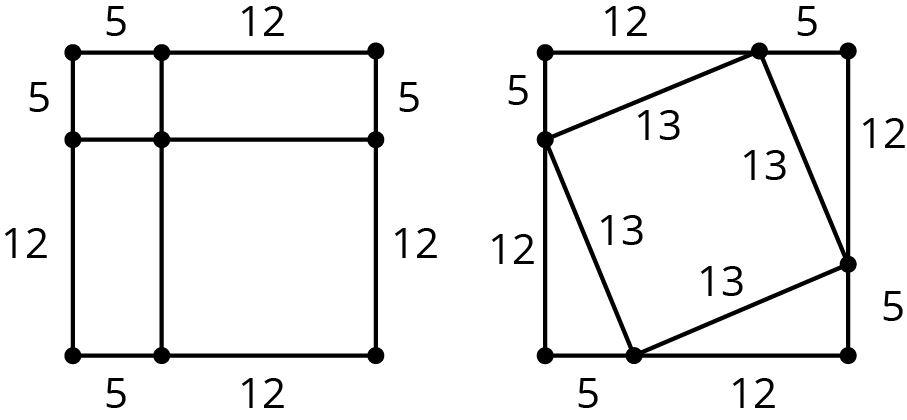
Problem 2
Use the areas of the two identical squares to explain why \(5^2+12^2=13^2\) without doing any calculations.
Problem 3
Each number is between which two consecutive integers?
-
\(\sqrt{10}\)
-
\(\sqrt{54}\)
-
\(\sqrt{18}\)
-
\(\sqrt{99}\)
-
\(\sqrt{41}\)
Problem 4
-
Give an example of a rational number, and explain how you know it is rational.
- Give three examples of irrational numbers.
Problem 5
Write each expression as a single power of 10.
- \(10^5 \boldcdot 10^0\)
- \(\frac{10^9}{10^0}\)
Problem 6
Andre is ordering ribbon to make decorations for a school event. He needs a total of exactly 50.25 meters of blue and green ribbon. Andre needs 50% more blue ribbon than green ribbon for the basic design, plus an extra 6.5 meters of blue ribbon for accents. How much of each color of ribbon does Andre need to order?