Lesson 12
Edge Lengths and Volumes
Let’s explore the relationship between volume and edge lengths of cubes.
12.1: Ordering Squares and Cubes
Let \(a\), \(b\), \(c\), \(d\), \(e\), and \(f\) be positive numbers.
Given these equations, arrange \(a\), \(b\), \(c\), \(d\), \(e\), and \(f\) from least to greatest. Explain your reasoning.
-
\(a^2 = 9\)
-
\(b^3 = 8\)
-
\(c^2 = 10\)
-
\(d^3 = 9\)
-
\(e^2 = 8\)
-
\(f^3 = 7\)
12.2: Name That Edge Length!
Fill in the missing values using the information provided:
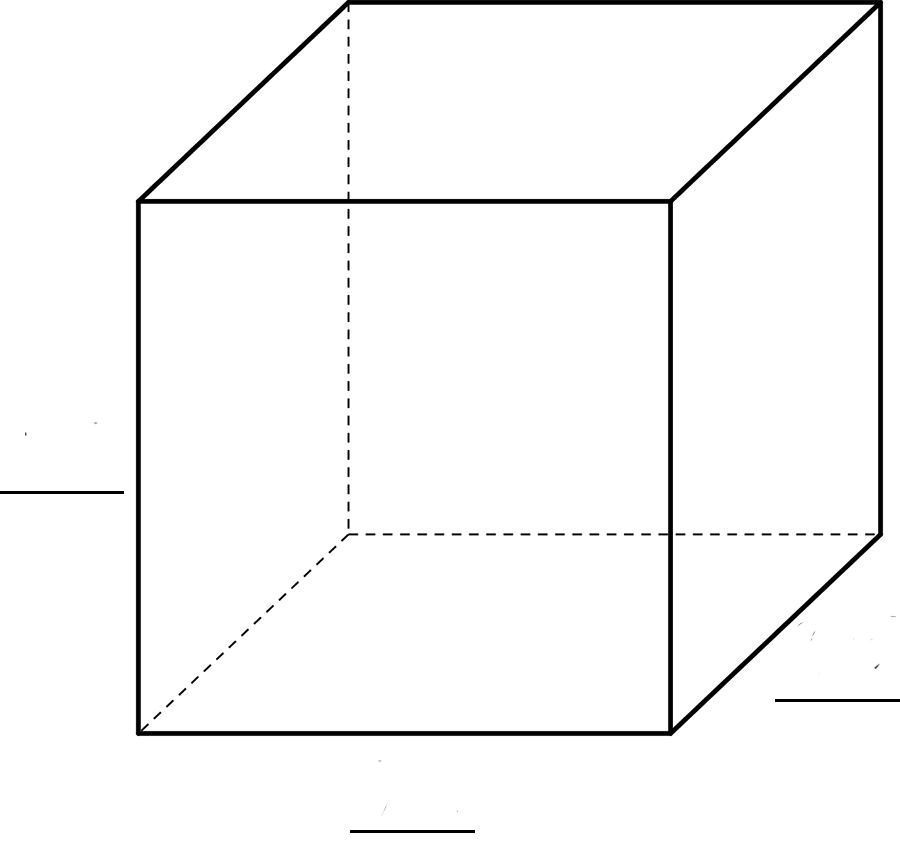
| sides | volume | volume equation |
|---|---|---|
| \(27\,\text{in}^3\) | ||
|
\(\sqrt[3]{5}\) |
||
| \((\sqrt[3]{16})^3=16\) |
A cube has a volume of 8 cubic centimeters. A square has the same value for its area as the value for the surface area of the cube. How long is each side of the square?
12.3: Card Sort: Rooted in the Number Line
Your teacher will give your group a set of cards. For each card with a letter and value, find the two other cards that match. One shows the location on a number line where the value exists, and the other shows an equation that the value satisfies. Be prepared to explain your reasoning.
Summary
To review, the side length of the square is the square root of its area. In this diagram, the square has an area of 16 units and a side length of 4 units.
These equations are both true: \(\displaystyle 4^2=16\) \(\displaystyle \sqrt{16}=4\)

Now think about a solid cube. The cube has a volume, and the edge length of the cube is called the cube root of its volume. In this diagram, the cube has a volume of 64 units and an edge length of 4 units:
These equations are both true:
\(\displaystyle 4^3=64\)
\(\displaystyle \sqrt[3]{64}=4\)
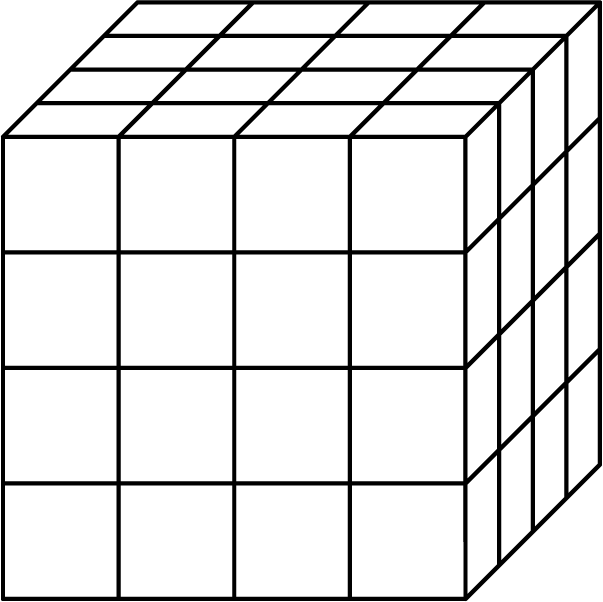
\(\sqrt[3]{64}\) is pronounced “The cube root of 64.” Here are some other values of cube roots:
\(\sqrt[3]{8}=2\), because \(2^3=8\)
\(\sqrt[3]{27}=3\), because \(3^3=27\)
\(\sqrt[3]{125}=5\), because \(5^3=125\)
Glossary Entries
- cube root
The cube root of a number \(n\) is the number whose cube is \(n\). It is also the edge length of a cube with a volume of \(n\). We write the cube root of \(n\) as \(\sqrt[3]{n}\).
For example, the cube root of 64, written as \(\sqrt[3]{64}\), is 4 because \(4^3\) is 64. \(\sqrt[3]{64}\) is also the edge length of a cube that has a volume of 64.