Lesson 12
Edge Lengths and Volumes
Let’s explore the relationship between volume and edge lengths of cubes.
Problem 1
- What is the volume of a cube with a side length of
- 4 centimeters?
- \(\sqrt[3]{11}\) feet?
- \(s\) units?
- What is the side length of a cube with a volume of
- 1,000 cubic centimeters?
- 23 cubic inches?
- \(v\) cubic units?
Problem 2
Write an equivalent expression that doesn’t use a cube root symbol.
- \(\sqrt[3]{1}\)
- \(\sqrt[3]{216}\)
- \(\sqrt[3]{8000}\)
- \(\sqrt[3]{\frac{1}{64}}\)
- \(\sqrt[3]{\frac{27}{125}}\)
- \(\sqrt[3]{0.027}\)
- \(\sqrt[3]{0.000125}\)
Problem 3
Find the distance between each pair of points. If you get stuck, try plotting the points on graph paper.
- \(X=(5,0)\) and \(Y=(\text-4,0)\)
-
\(K=(\text-21,\text-29)\) and \(L=(0,0)\)
Problem 4
Here is a 15-by-8 rectangle divided into triangles. Is the shaded triangle a right triangle? Explain or show your reasoning.

Problem 5
Here is an equilateral triangle. The length of each side is 2 units. A height is drawn. In an equilateral triangle, the height divides the opposite side into two pieces of equal length.
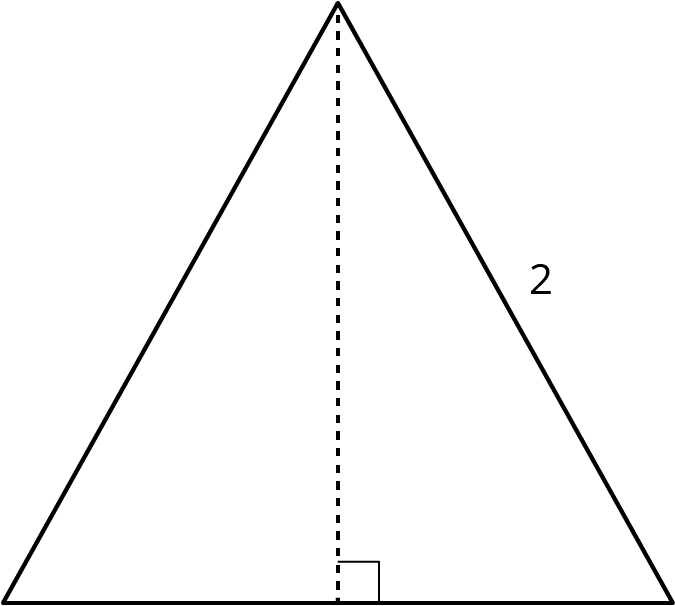
- Find the exact height.
- Find the area of the equilateral triangle.
- (Challenge) Using \(x\) for the length of each side in an equilateral triangle, express its area in terms of \(x\).