Lesson 9

Moves in Parallel

Let’s transform some lines.

Problem 1

  1. Draw parallel lines \(AB\) and \(CD\).
  2. Pick any point \(E\). Rotate \(AB\) 90 degrees clockwise around \(E\).
  3. Rotate line \(CD\) 90 degrees clockwise around \(E\).
  4. What do you notice?

Problem 2

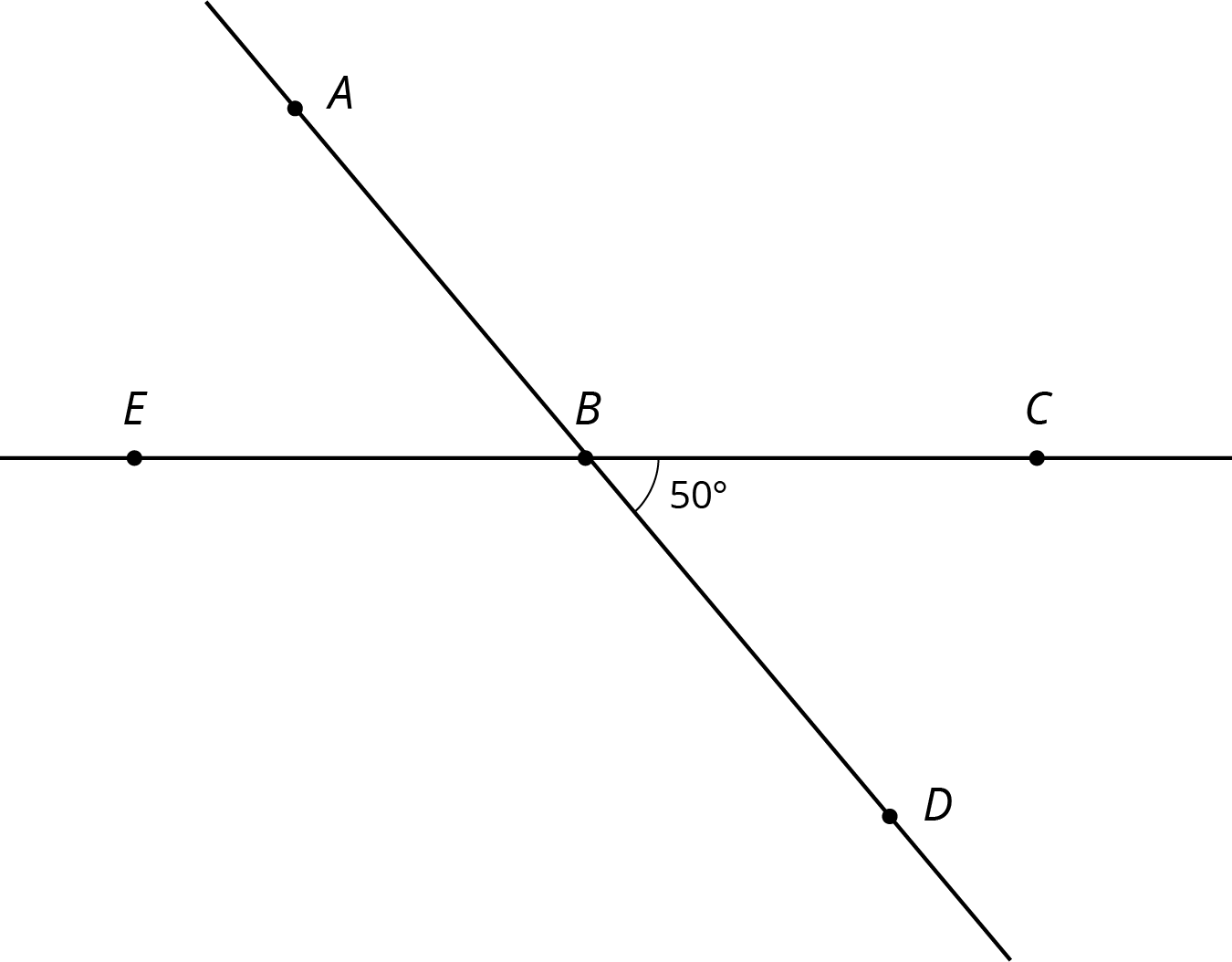
Use the diagram to find the measures of each angle. Explain your reasoning.

  1. \(m{\angle ABC}\)
  2. \(m{\angle EBD}\)
  3. \(m{\angle ABE}\)
Lines A D and E C intersect at point B. Angle C B D is 50 degrees.

Problem 3

Points \(P\) and \(Q\) are plotted on a line.

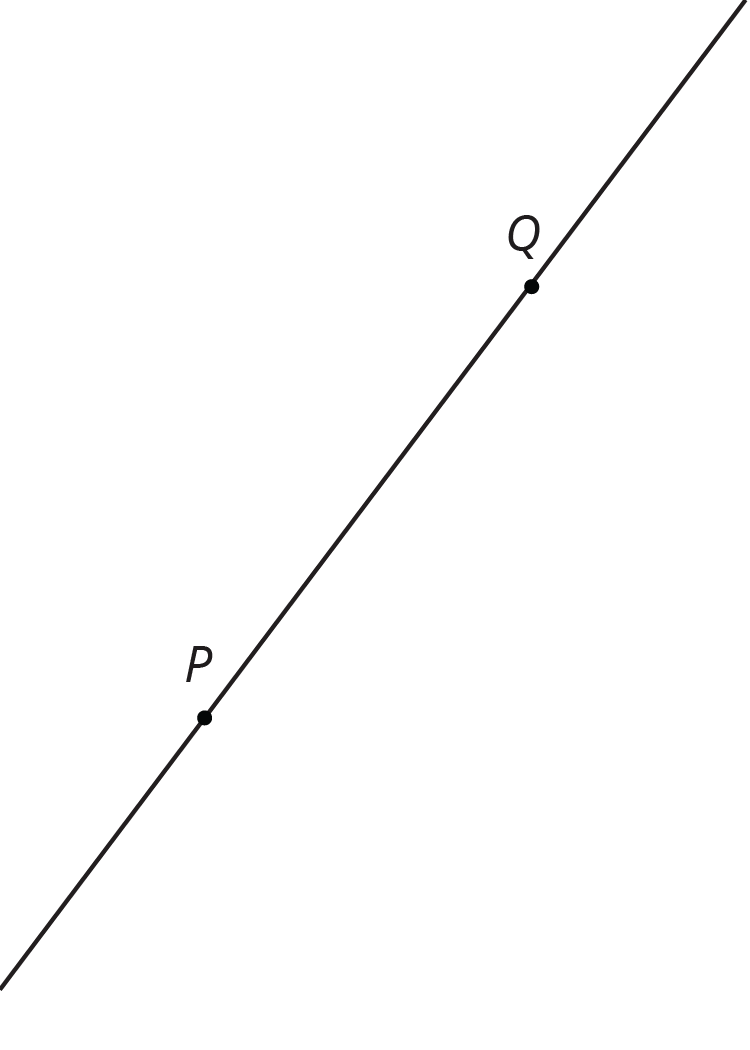
A line that slants upward and to the right with two plots labeled P and Q pointed on it. Point P is below point Q.
  1. Find a point \(R\) so that a 180-degree rotation with center \(R\) sends \(P\) to \(Q\) and \(Q\) to \(P\).
  2. Is there more than one point \(R\) that works for part a?

Problem 4

In the picture triangle \(A’B’C’\) is an image of triangle \(ABC\) after a rotation. The center of rotation is \(D\).

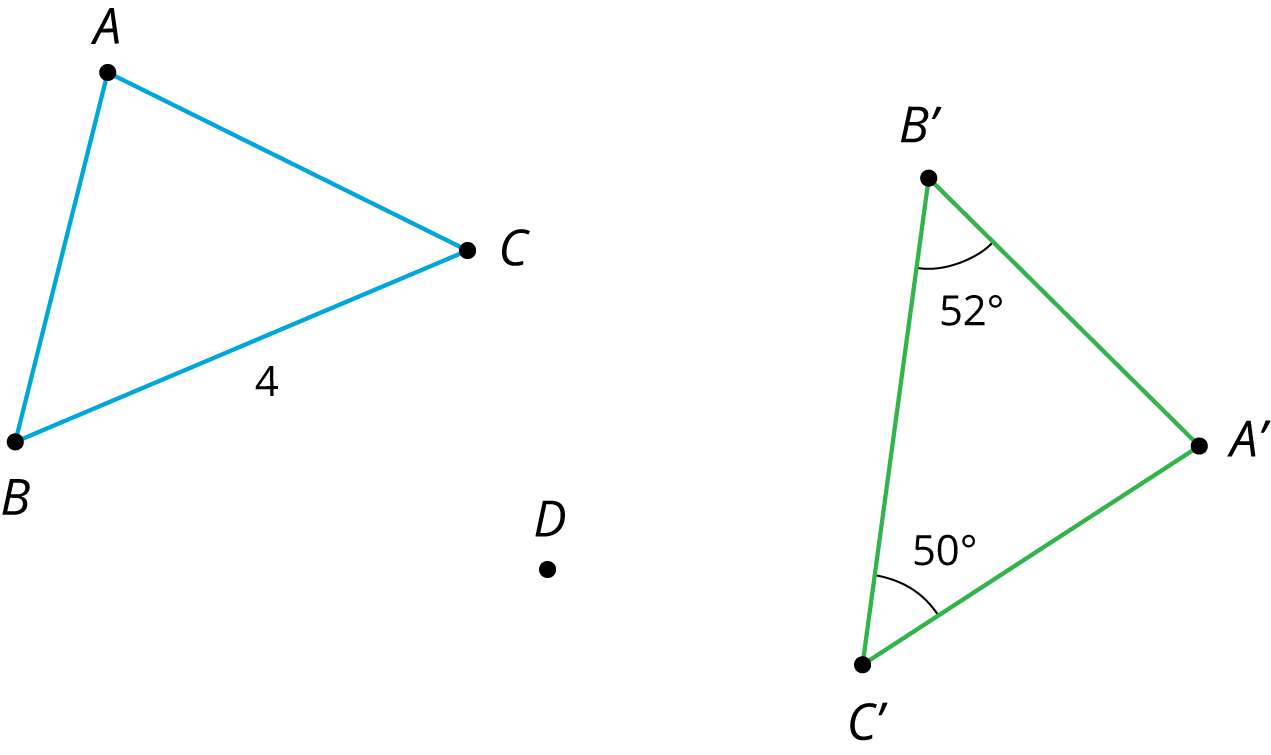
A triangle A B C and its image, triangle A prime B prime C prime and a point D. Side B C is 4, angle C prime is 50 degrees and angle B prime is 52 degrees. 
  1. What is the length of side \(B’C’\)? Explain how you know.
  2. What is the measure of angle \(B\)? Explain how you know.
  3. What is the measure of angle \(C\)? Explain how you know.
(From Unit 1, Lesson 7.)

Problem 5

The point \((\text-4,1)\) is rotated 180 degrees counterclockwise using center \((0,0)\). What are the coordinates of the image?

A:

\((\text-1,\text-4)\)

B:

\((\text-1,4)\)

C:

\((4,1)\)

D:

\((4,\text-1)\)

(From Unit 1, Lesson 6.)