Lesson 11
What Is the Same?
Let’s decide whether shapes are the same.
11.1: Find the Right Hands
A person’s hands are mirror images of each other. In the diagram, a left hand is labeled. Shade all of the right hands.

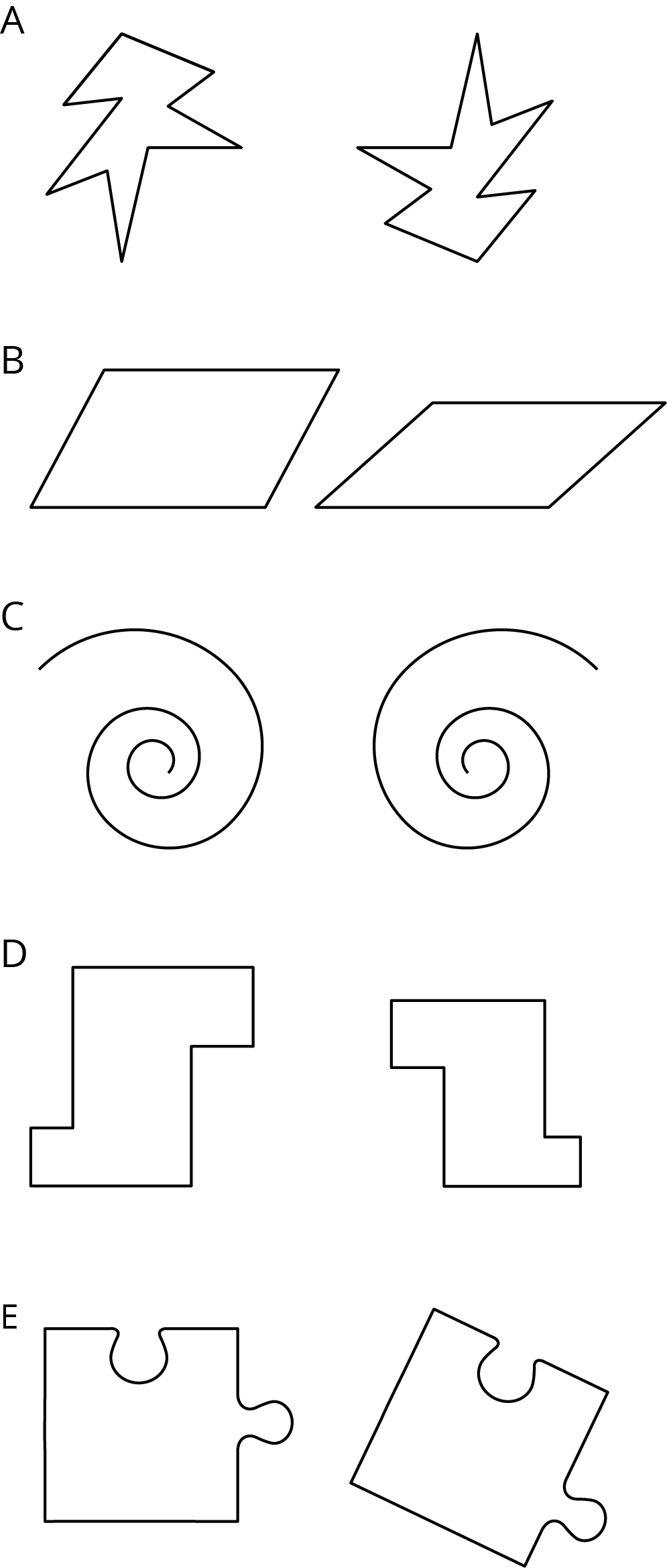
11.2: Are They the Same?
For each pair of shapes, decide whether or not they are the same.
11.3: Area, Perimeter, and Congruence
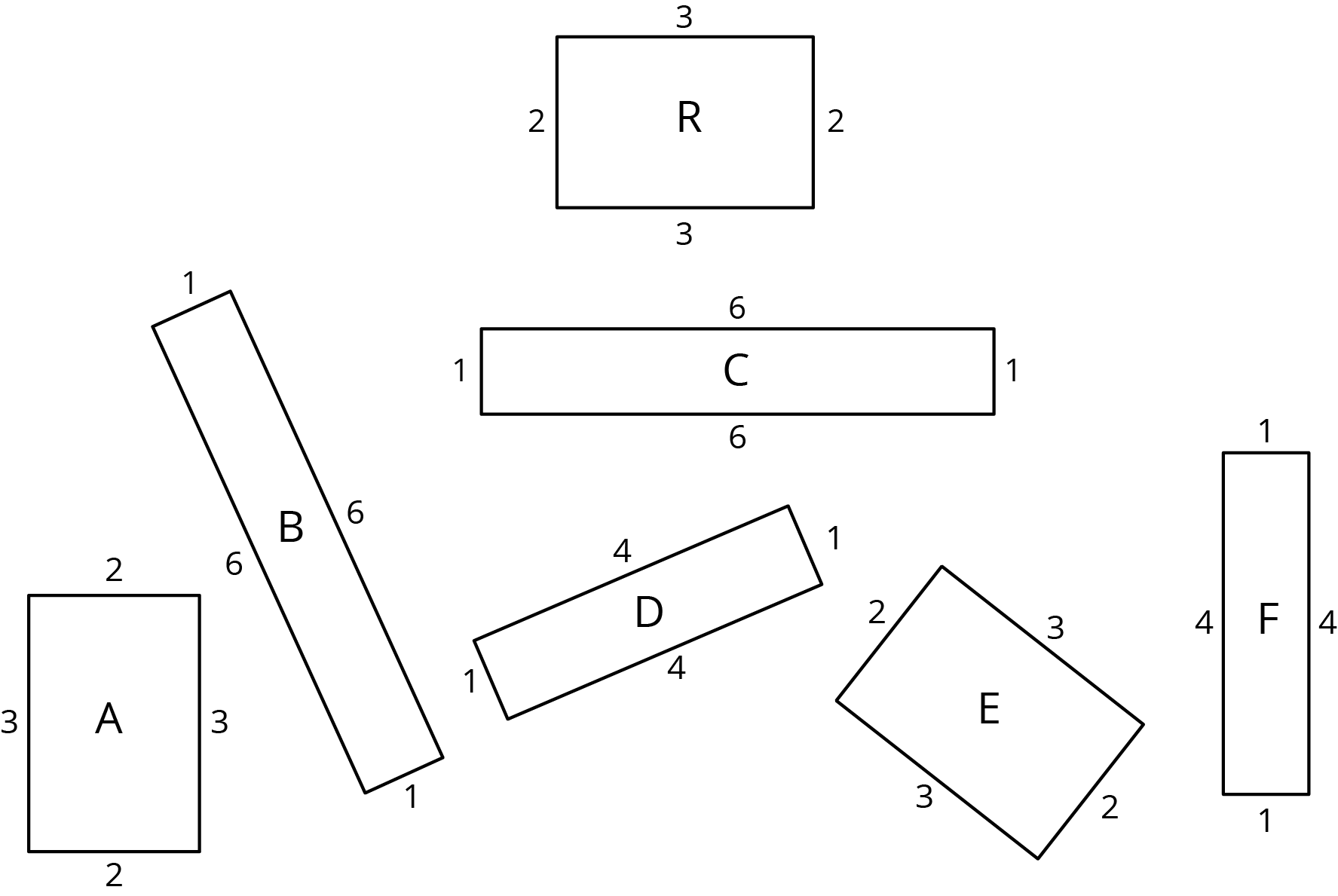
- Which of these rectangles have the same area as Rectangle R but different perimeter?
- Which rectangles have the same perimeter as Rectangle R but different area?
- Which have the same area and the same perimeter as Rectangle R?
- Use materials from the geometry tool kit to decide which rectangles are congruent. Shade congruent rectangles with the same color.
In square \(ABCD\), points \(E\), \(F\), \(G\), and \(H\) are midpoints of their respective sides. What fraction of square \(ABCD\) is shaded? Explain your reasoning.

Summary
Congruent is a new term for an idea we have already been using. We say that two figures are congruent if one can be lined up exactly with the other by a sequence of rigid transformations. For example, triangle \(EFD\) is congruent to triangle \(ABC\) because they can be matched up by reflecting triangle \(ABC\) across \(AC\) followed by the translation shown by the arrow. Notice that all corresponding angles and side lengths are equal.

Here are some other facts about congruent figures:
-
We don’t need to check all the measurements to prove two figures are congruent; we just have to find a sequence of rigid transformations that match up the figures.
-
A figure that looks like a mirror image of another figure can be congruent to it. This means there must be a reflection in the sequence of transformations that matches up the figures.
-
Since two congruent polygons have the same area and the same perimeter, one way to show that two polygons are not congruent is to show that they have a different perimeter or area.
Glossary Entries
- congruent
One figure is congruent to another if it can be moved with translations, rotations, and reflections to fit exactly over the other.
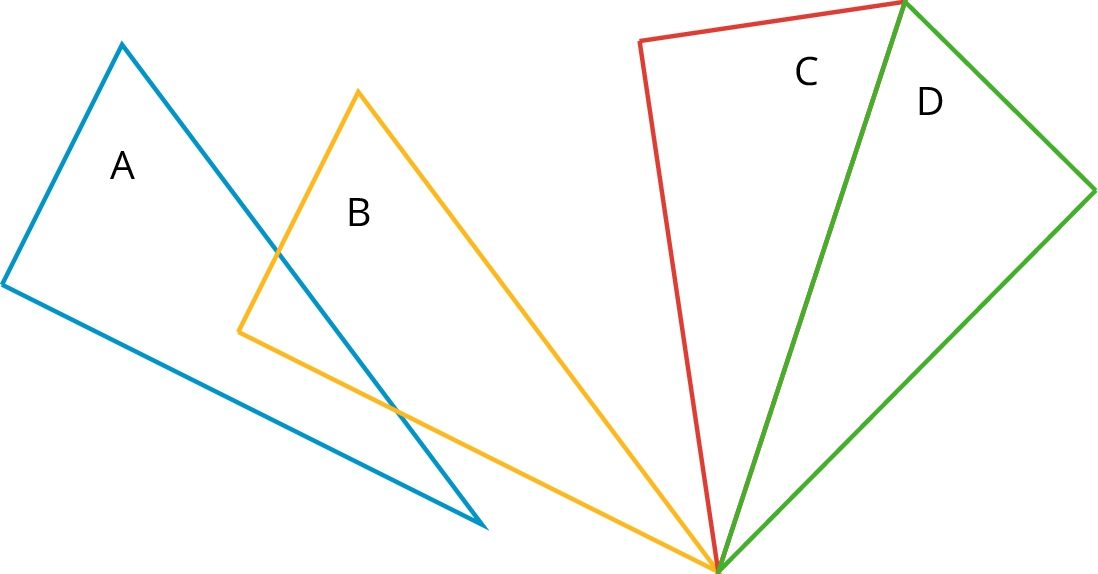
In the figure, Triangle A is congruent to Triangles B, C, and D. A translation takes Triangle A to Triangle B, a rotation takes Triangle B to Triangle C, and a reflection takes Triangle C to Triangle D.