Lesson 13

Congruence

Let’s find ways to test congruence of interesting figures.

13.1: Not Just the Vertices

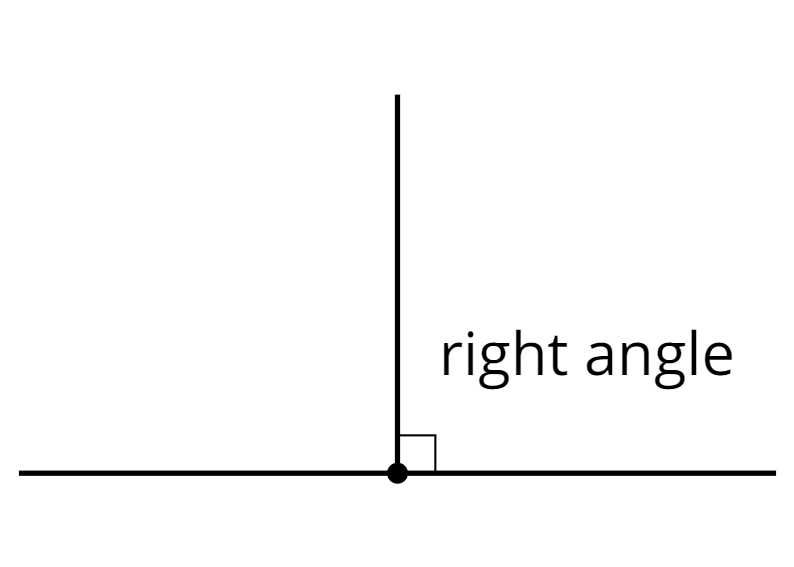
Trapezoids \(ABCD\) and \(A’B’C’D’\) are congruent.

  • Draw and label the points on \(A’B’C’D’\) that correspond to \(E\) and \(F\).
  • Draw and label the points on \(ABCD\) that correspond to \(G’\) and \(H’\).
  • Draw and label at least three more pairs of corresponding points.
Two trapezoids A B C D and its image A prime B prime C prime D prime on a square grid.

13.2: Congruent Ovals

Are any of the ovals congruent to one another? Explain how you know.

Four ovals on a square grid. There is one pair of small ovals and one pair of larger ovals. Each pair has the long length in the horizontal and vertical orientation.


You can use 12 toothpicks to create a polygon with an area of five square toothpicks, like this:

Can you use exactly 12 toothpicks to create a polygon with an area of four square toothpicks?

A twelve sided figure in a grid.

13.3: Corresponding Points in Congruent Figures

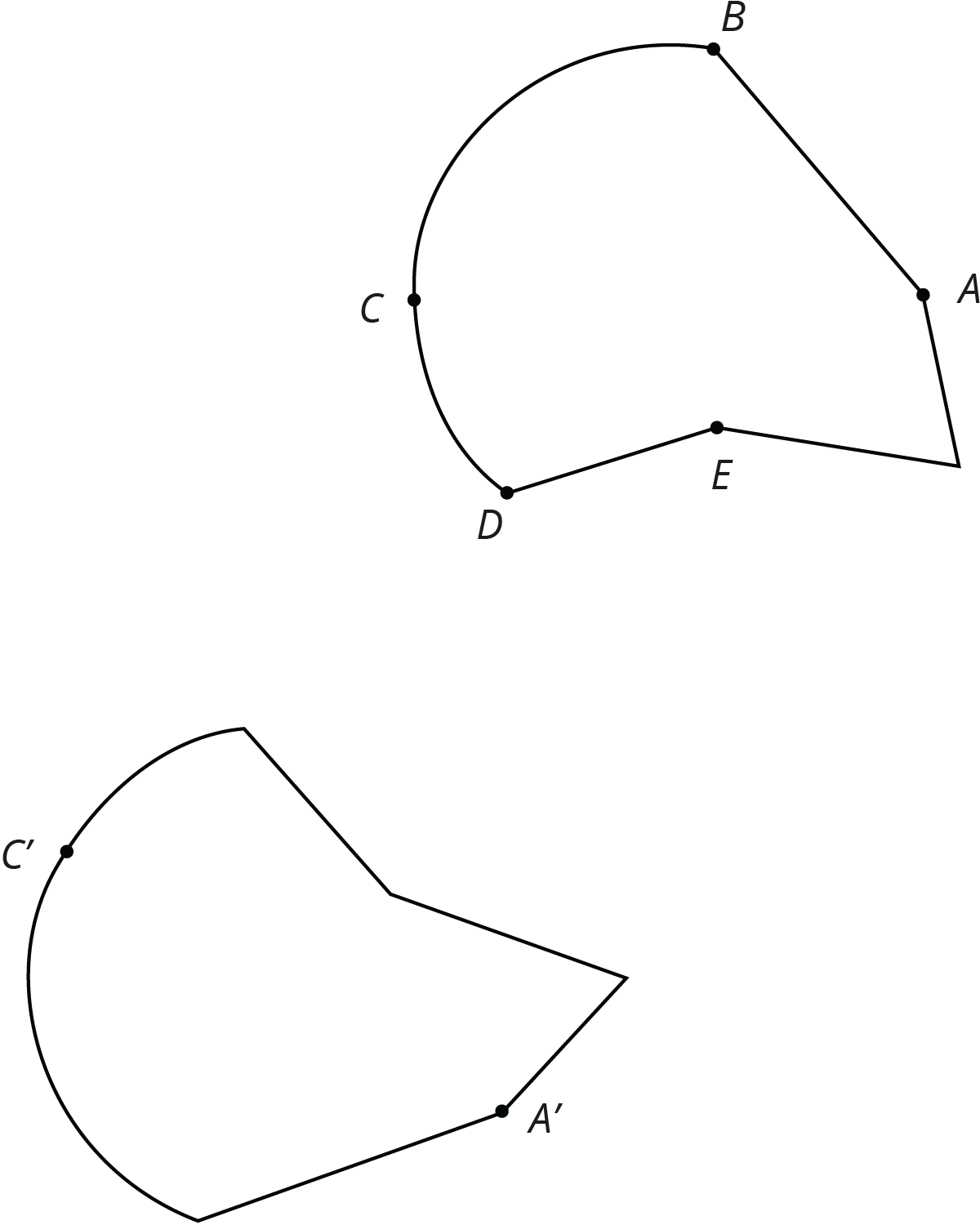
Here are two congruent shapes with some corresponding points labeled.

Figure A B C D E and its image A prime B prime C prime D prime E prime. The image has been reflected and has points A prime and C prime.

  1. Draw the points corresponding to \(B\), \(D\), and \(E\), and label them \(B’\), \(D’\), and \(E’\).

  2. Draw line segments \(AD\) and \(A’D’\) and measure them. Do the same for segments \(BC\) and \(B’C’\) and for segments \(AE\) and \(A’E’\). What do you notice?

  3. Do you think there could be a pair of corresponding segments with different lengths? Explain.

13.4: Astonished Faces

Are these faces congruent? Explain your reasoning.

Two faces on a square grid. The heads are the same size, as are the mouths and the eyes. The eyes are closer together and the smile is higher on the left face.

 

Summary

To show two figures are congruent, you align one with the other by a sequence of rigid transformations. This is true even for figures with curved sides. Distances between corresponding points on congruent figures are always equal, even for curved shapes. For example, corresponding segments \(AB\) and \(A'B'\) on these congruent ovals have the same length:

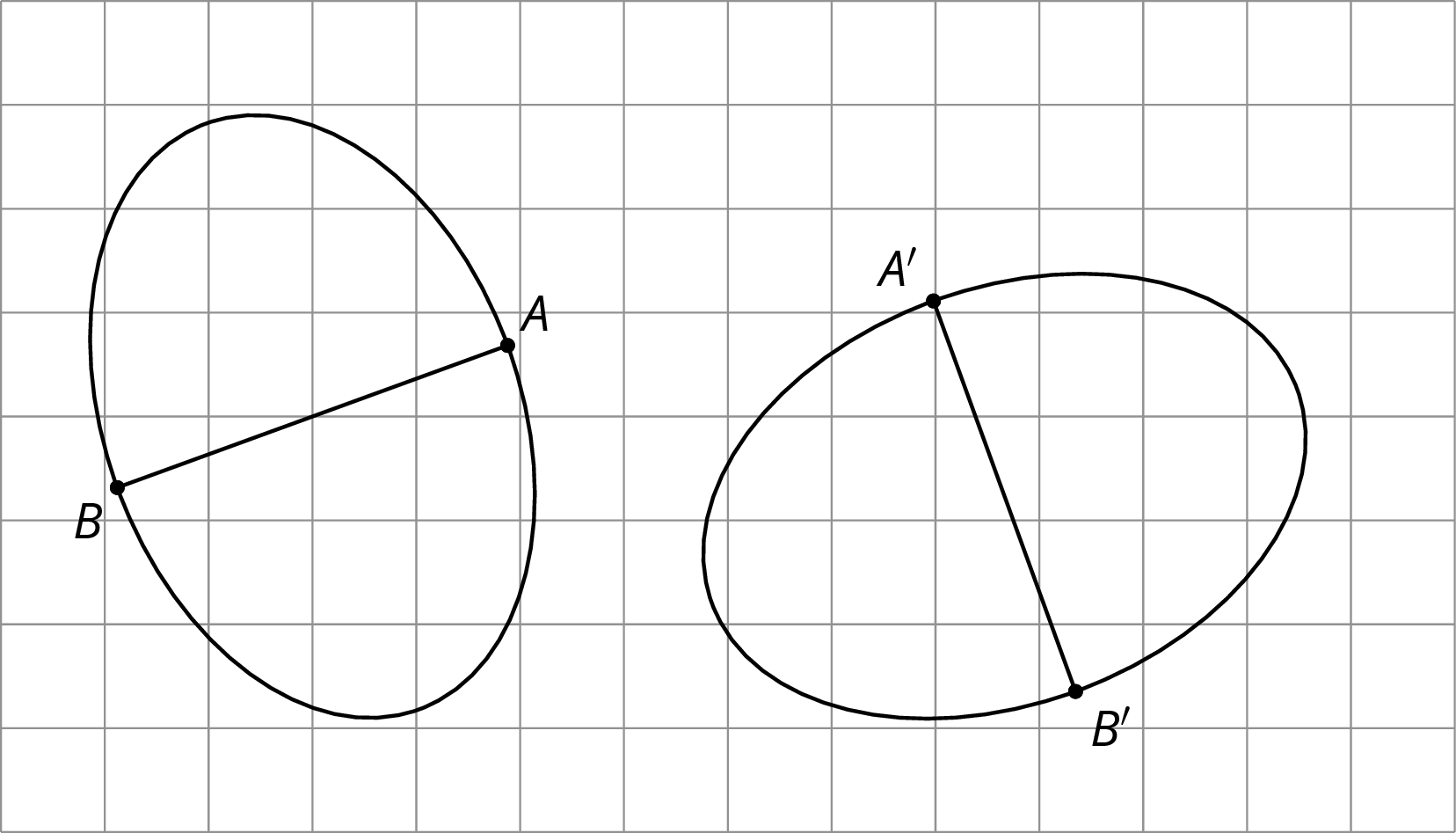
Two congruent ovals on a square grid.

To show two figures are not congruent, you can find parts of the figures that should correspond but that have different measurements.

For example, these two ovals don’t look congruent.

Two ovals on a grid. The first is 5 units wide and 4 units tall. The second is skewed to the right.

On both, the longest distance is 5 units across, and the longest distance from top to bottom is 4 units. The line segment from the highest to lowest point is in the middle of the left oval, but in the right oval, it’s 2 units from the right end and 3 units from the left end. This proves they are not congruent.

Two ovals on a grid. The first is 5 units wide and 4 units tall. The second is skewed to the right.

Video Summary

Video VLS G8U1V3 Congruence (Lessons 11–13) available at https://player.vimeo.com/video/442078342.

Glossary Entries

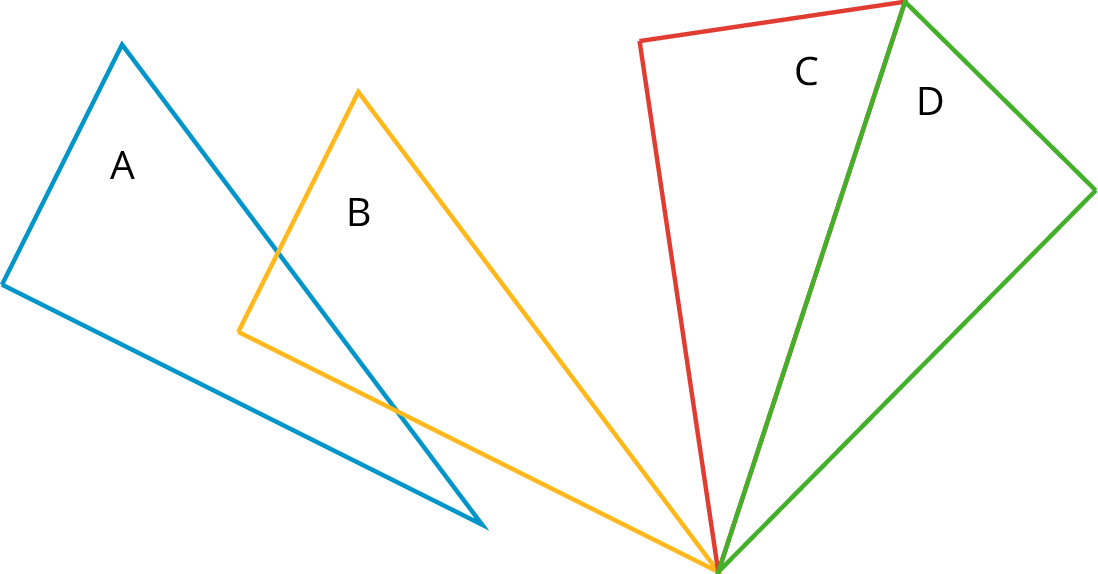
  • congruent

    One figure is congruent to another if it can be moved with translations, rotations, and reflections to fit exactly over the other.

    In the figure, Triangle A is congruent to Triangles B, C, and D. A translation takes Triangle A to Triangle B, a rotation takes Triangle B to Triangle C, and a reflection takes Triangle C to Triangle D.

     

    four congruent triangles

     

  • right angle

    A right angle is half of a straight angle. It measures 90 degrees.

    a right angle