Lesson 8

Rotation Patterns

Let’s rotate figures in a plane.

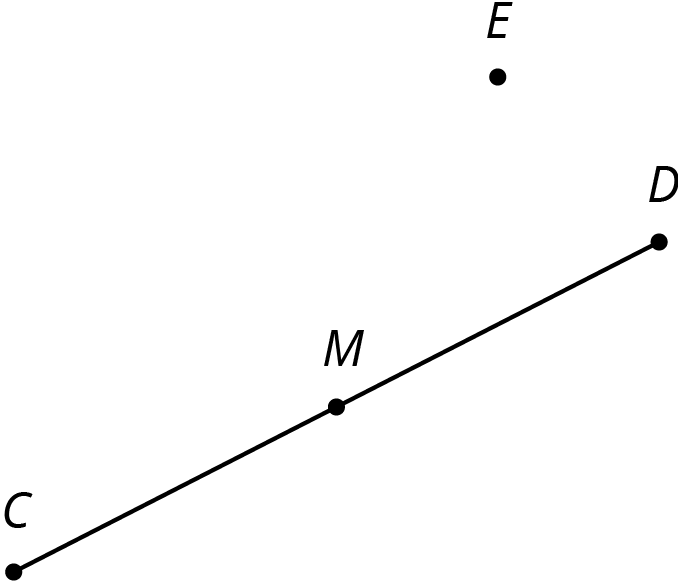
Problem 1

For the figure shown here,

  1. Rotate segment \(CD\) \(180^\circ\) around point \(D\).
  2. Rotate segment \(CD\) \(180^\circ\) around point \(E\).
  3. Rotate segment \(CD\) \(180^\circ\) around point \(M\).
Segment C D with midpoint M and C D rising from left to right. Point E is above M D, slightly left of point D.

 

Problem 2

Here is an isosceles right triangle:

Draw these three rotations of triangle \(ABC\) together.

  1. Rotate triangle \(ABC\) 90 degrees clockwise around \(A\).
  2. Rotate triangle \(ABC\) 180 degrees around \(A\).
  3. Rotate triangle \(ABC\) 270 degrees clockwise around \(A\).
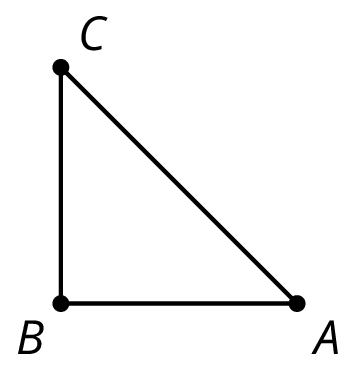
Right isosceles triangle A B C has horizonatl side A B with point A to the right of B, and has vertical side B C with point C directly above point B.

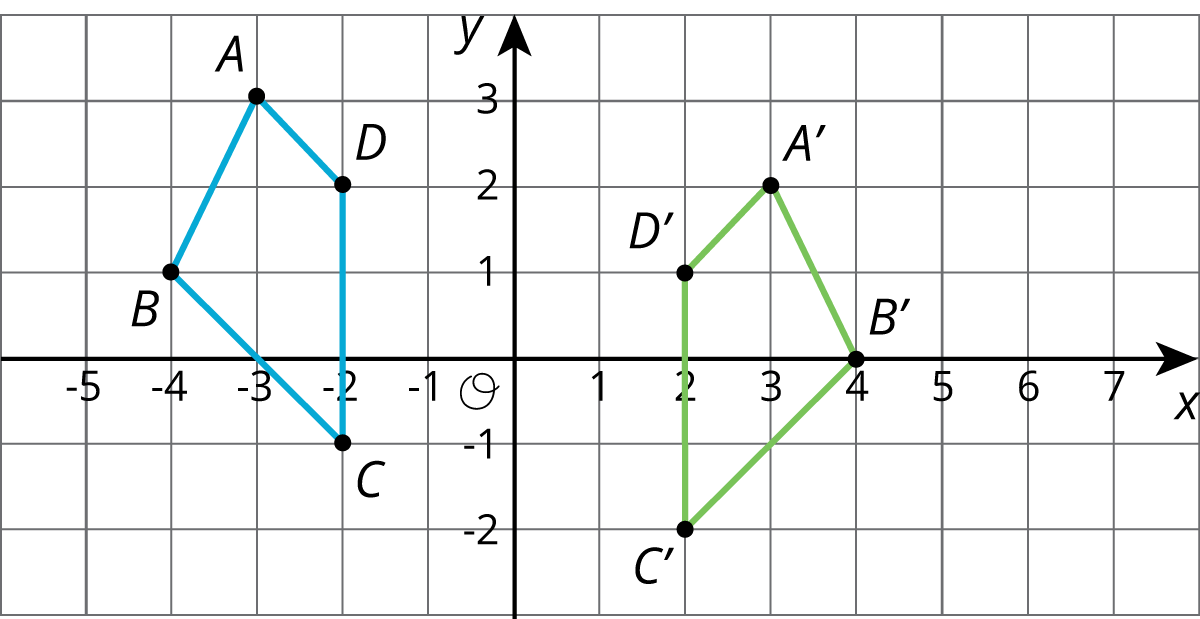
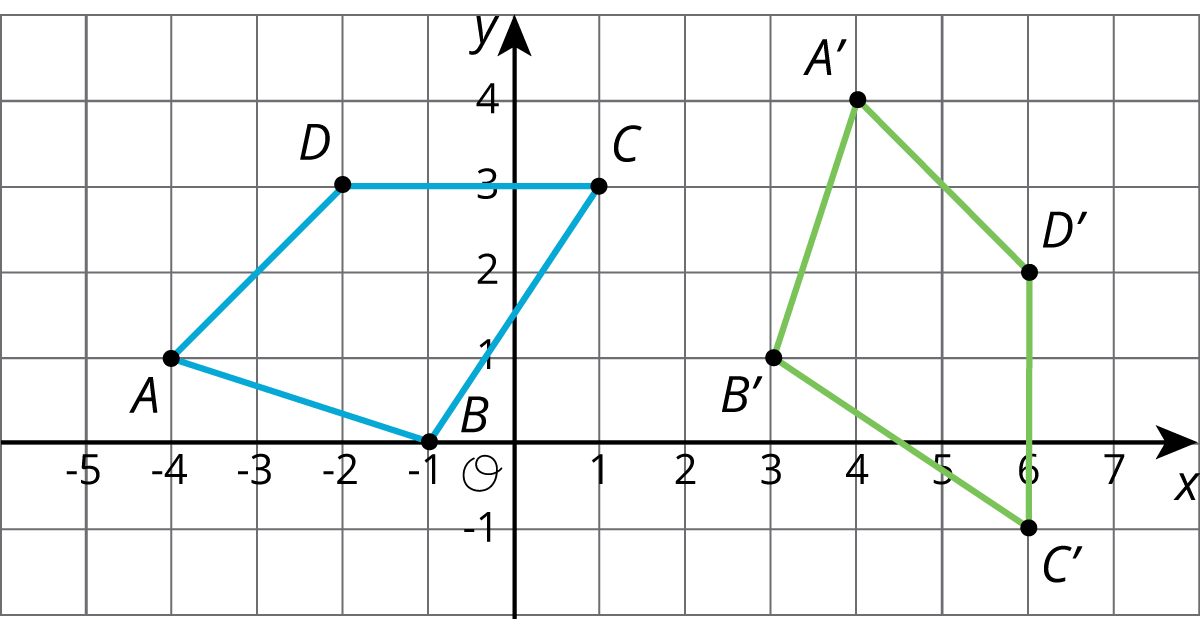
Problem 3

Each graph shows two polygons \(ABCD\) and \(A’B’C’D’\). In each case, describe a sequence of transformations that takes \(ABCD\) to \(A’B’C’D’\).

  1.  
    Quadrilateral \(A \ B\ C\ D\) and its image quadrilateral \(A\ prime\ B\ prime\ C\ prime\ D\ prime\)  on a coordinate plane, origin \(O\).
  2.  
    Quadrilateral \(A\ B\ C\ D\) and its image quadrilateral \(A\ prime\ B\ prime\ C\ prime\) and \(D\ prime\) on a coordinate plane, origin \(O\).
(From Unit 1, Lesson 5.)

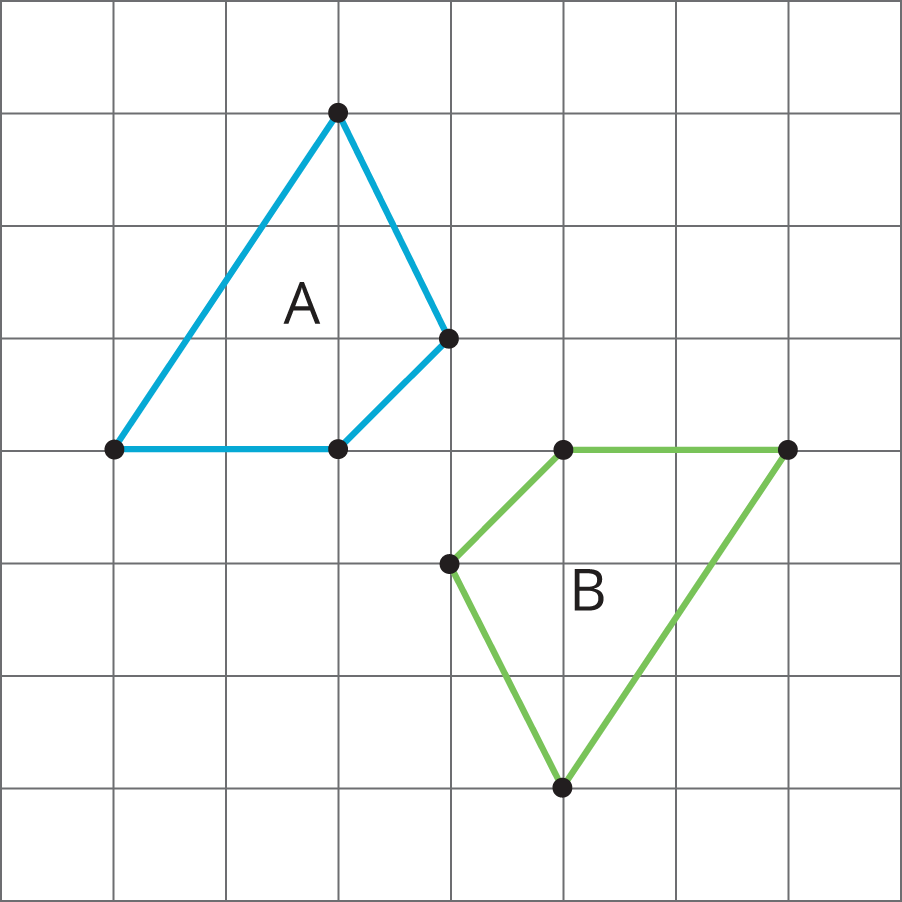
Problem 4

Lin says that she can map Polygon A to Polygon B using only reflections. Do you agree with Lin? Explain your reasoning.

Two quadrilaterals polygon A and B on a grid.
(From Unit 1, Lesson 4.)