Lesson 16

Parallel Lines and the Angles in a Triangle

Let’s see why the angles in a triangle add to 180 degrees.

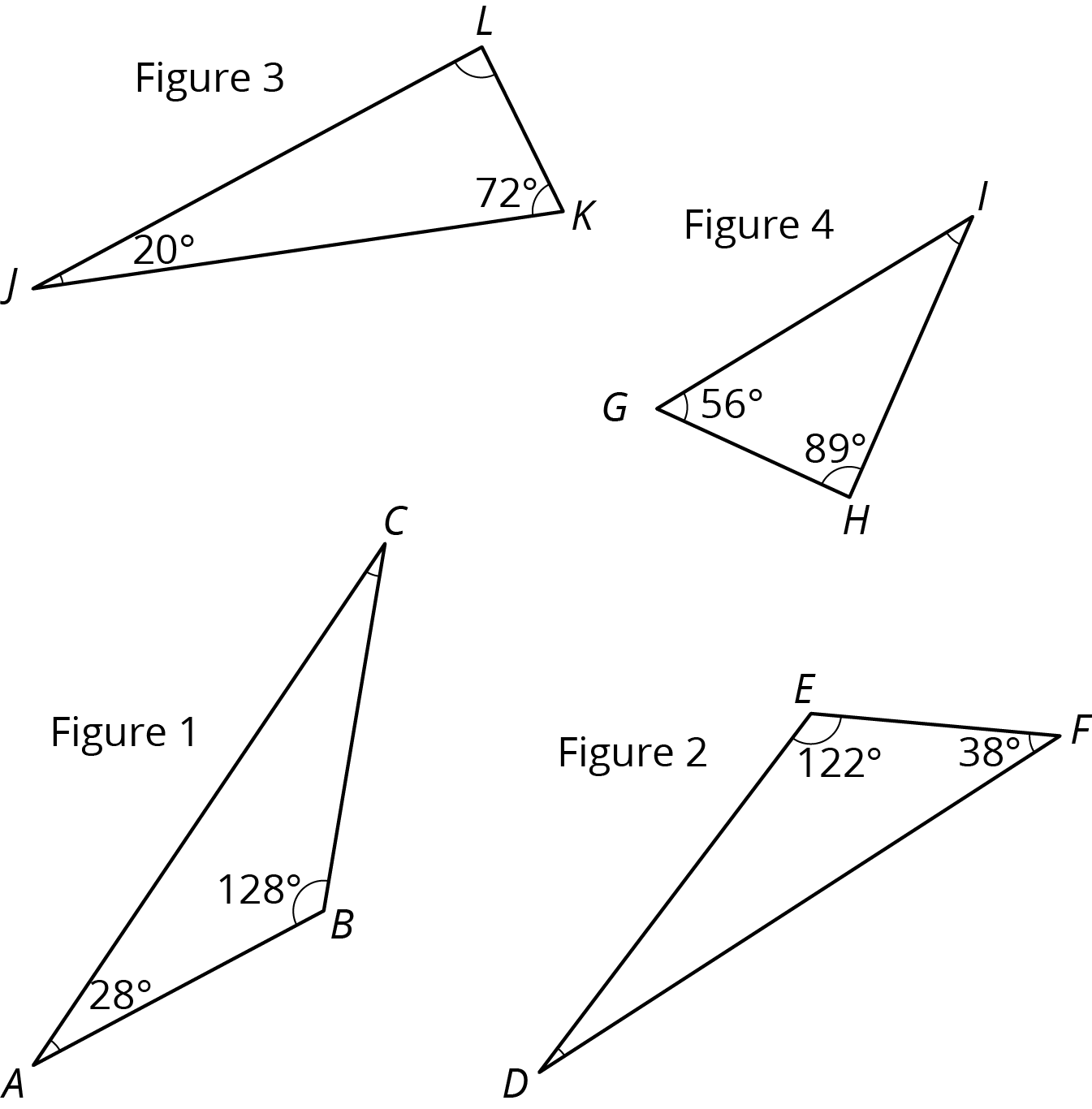
Problem 1

For each triangle, find the measure of the missing angle.

Four triangles. 

Problem 2

Is there a triangle with two right angles? Explain your reasoning.

Problem 3

In this diagram, lines \(AB\) and \(CD\) are parallel.

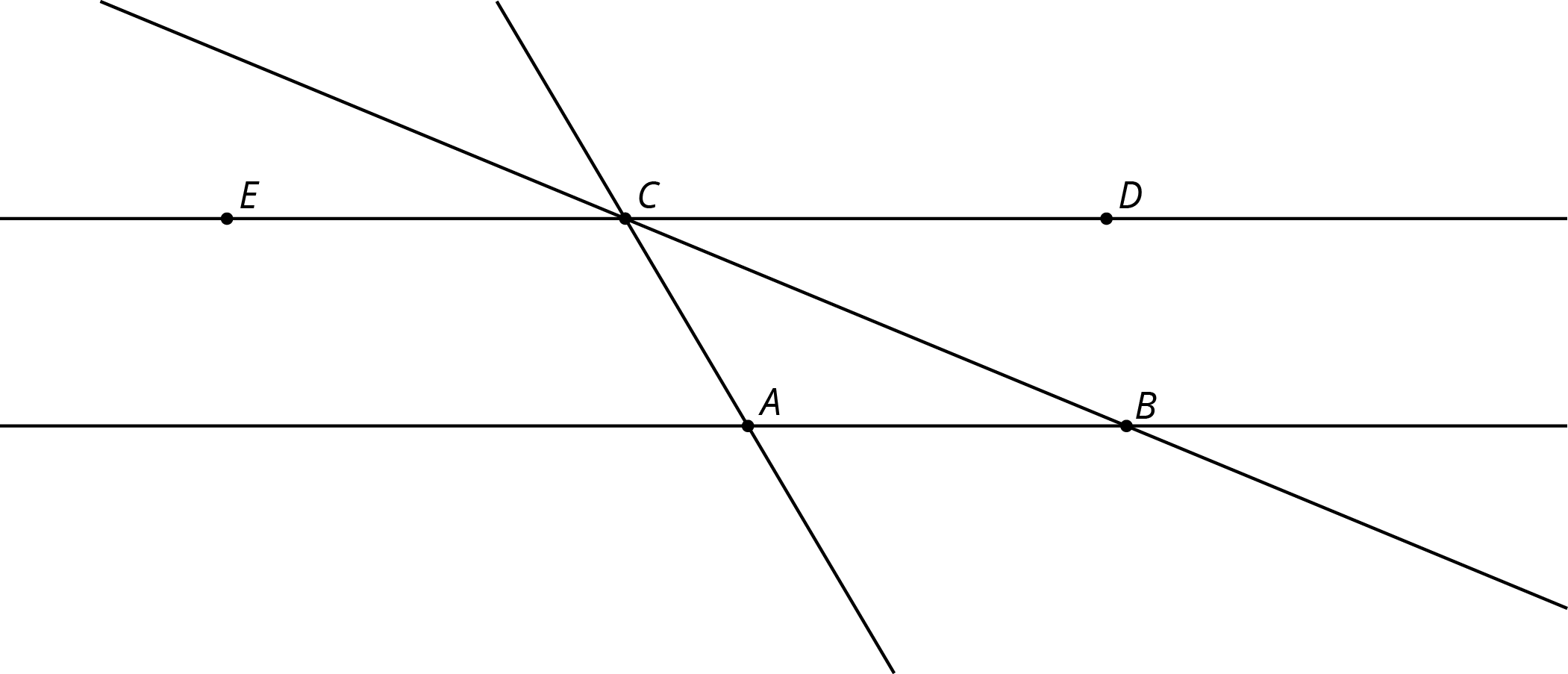
Four lines. Line A B. Line A C. Line C B. Line E D. Point C lies on line E D.

Angle \(ABC\) measures \(35^\circ\) and angle \(BAC\) measures \(115^\circ\).

  1. What is \(m{\angle ACE}\)?
  2. What is \(m{\angle DCB}\)?
  3. What is \(m{\angle ACB}\)?

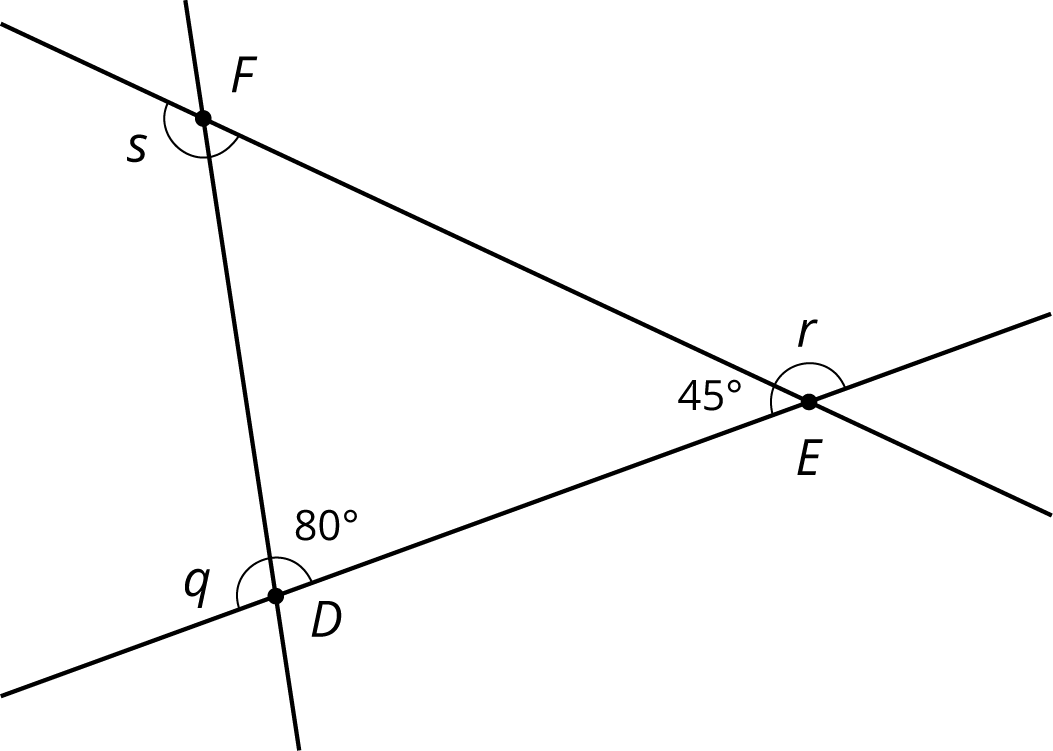
Problem 4

Here is a diagram of triangle \(DEF\).

  1. Find the measures of angles \(q\), \(r\), and \(s\).
  2. Find the sum of the measures of angles \(q\), \(r\), and \(s\).

  3. What do you notice about these three angles?

Three lines intersect to form Triangle D E F.

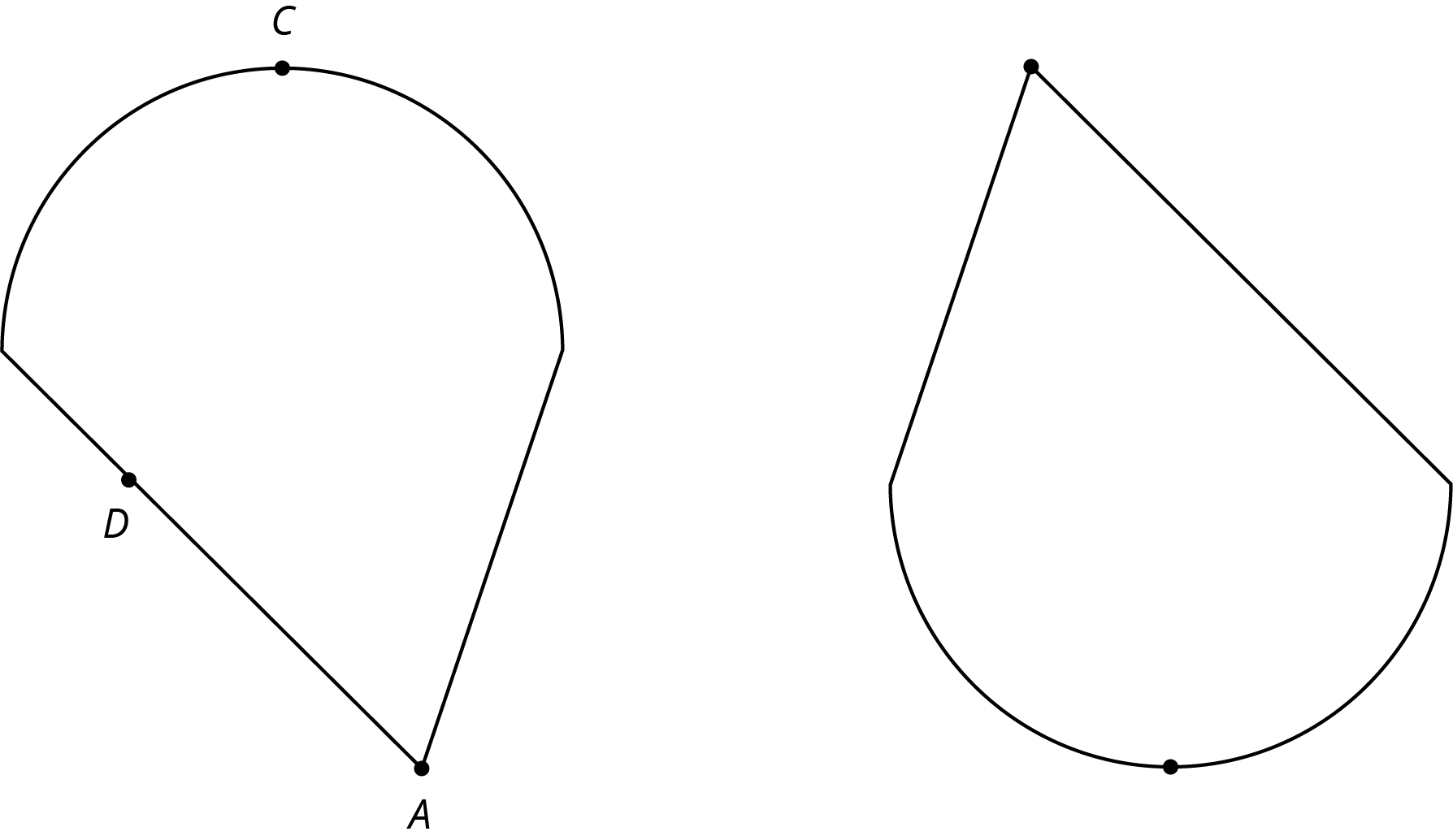
Problem 5

The two figures are congruent.

  1. Label the points \(A’\), \(B’\) and \(C’\) that correspond to \(A\), \(B\), and \(C\) in the figure on the right.
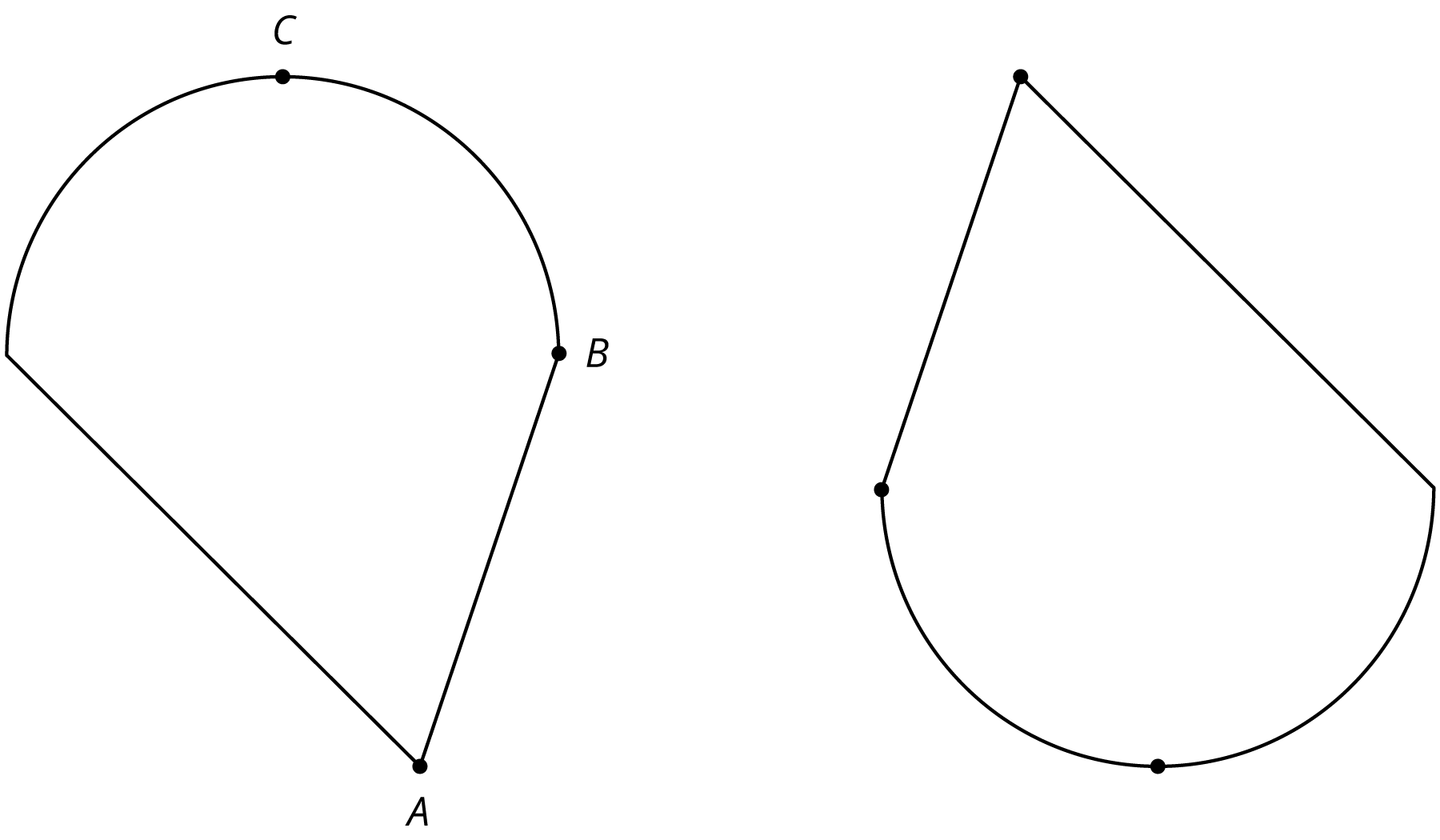
    Two congruent figures are semicircles with a connected opposite angle point.
  2. If segment \(AB\) measures 2 cm, how long is segment \(A’B’\)? Explain.
  3. The point \(D\) is shown in addition to \(A\) and \(C\). How can you find the point \(D’\) that corresponds to \(D\)? Explain your reasoning.
    Two congruent figures are semicircles with a connected opposite angle point.
(From Unit 1, Lesson 13.)