Lesson 15
Adding the Angles in a Triangle
Let’s explore angles in triangles.
Problem 1
In triangle \(ABC\), the measure of angle \(A\) is \(40^\circ\).
- Give possible measures for angles \(B\) and \(C\) if triangle \(ABC\) is isosceles.
- Give possible measures for angles \(B\) and \(C\) if triangle \(ABC\) is right.
Problem 2
For each set of angles, decide if there is a triangle whose angles have these measures in degrees:
- 60, 60, 60
- 90, 90, 45
- 30, 40, 50
- 90, 45, 45
- 120, 30, 30
If you get stuck, consider making a line segment. Then use a protractor to measure angles with the first two angle measures.
Problem 3
Angle \(A\) in triangle \(ABC\) is obtuse. Can angle \(B\) or angle \(C\) be obtuse? Explain your reasoning.
Problem 4
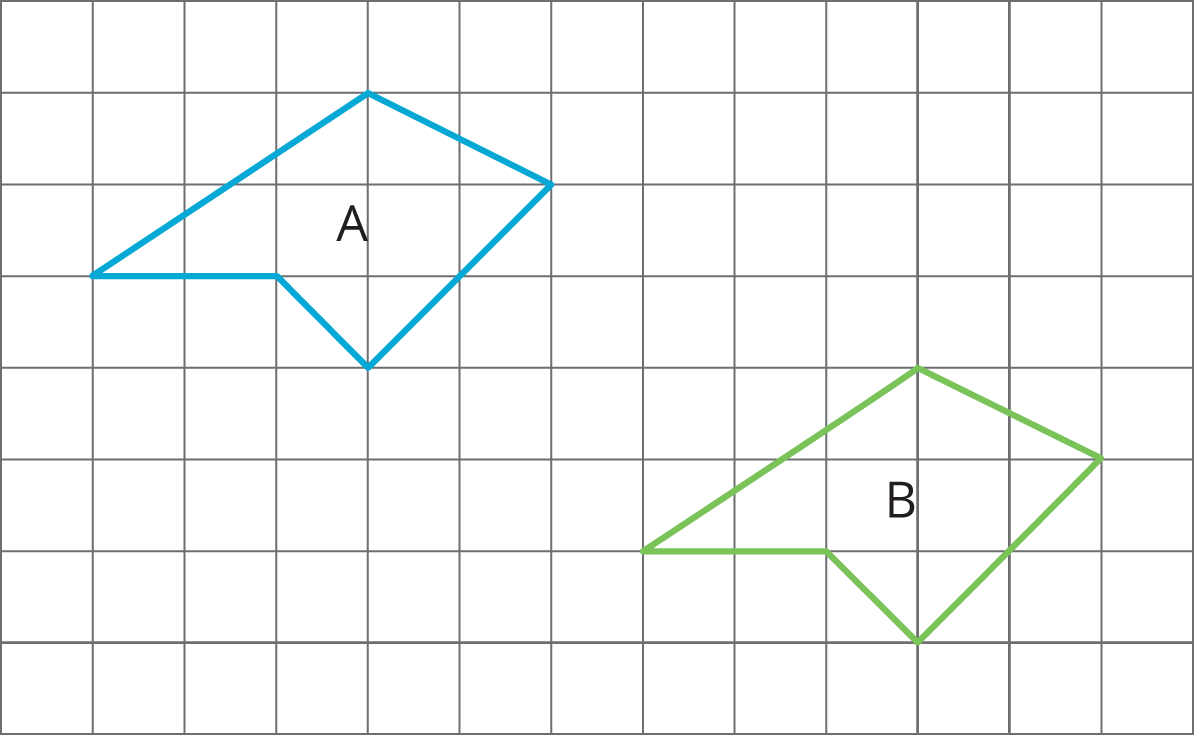
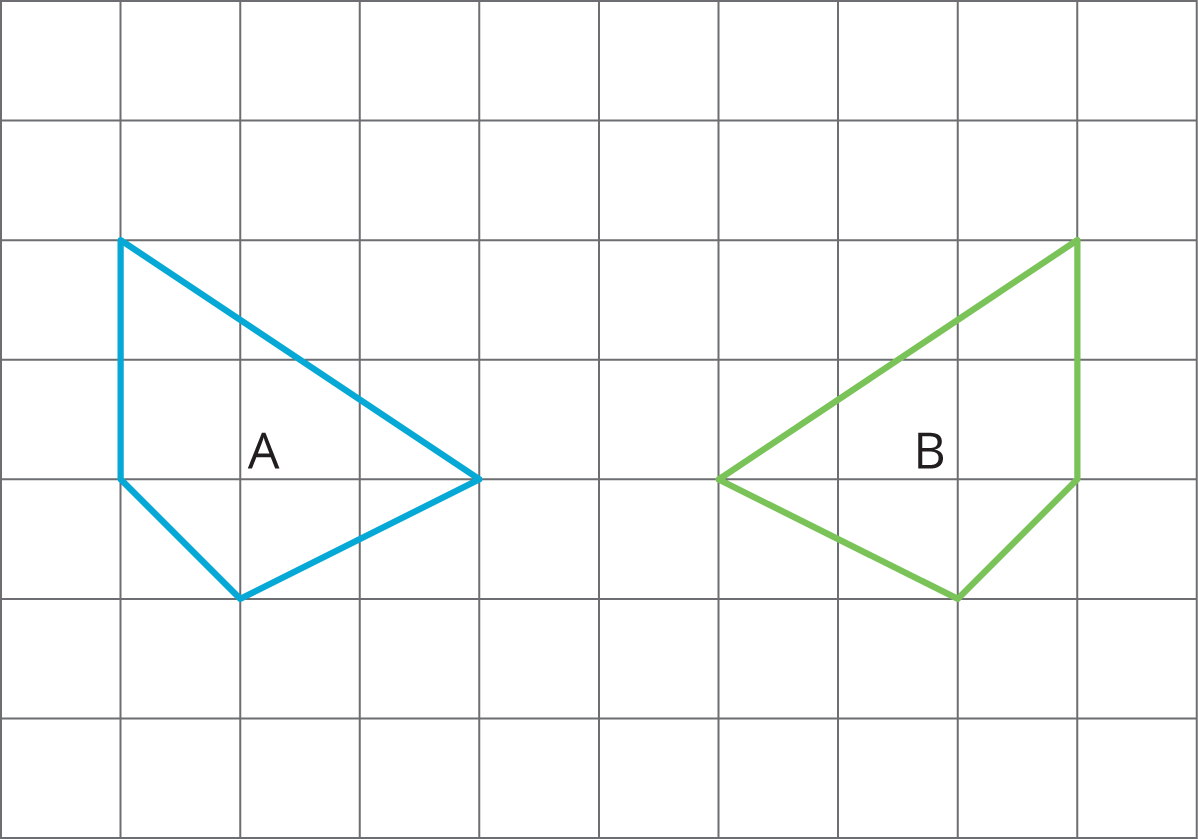
For each pair of polygons, describe the transformation that could be applied to Polygon A to get Polygon B.
Problem 5
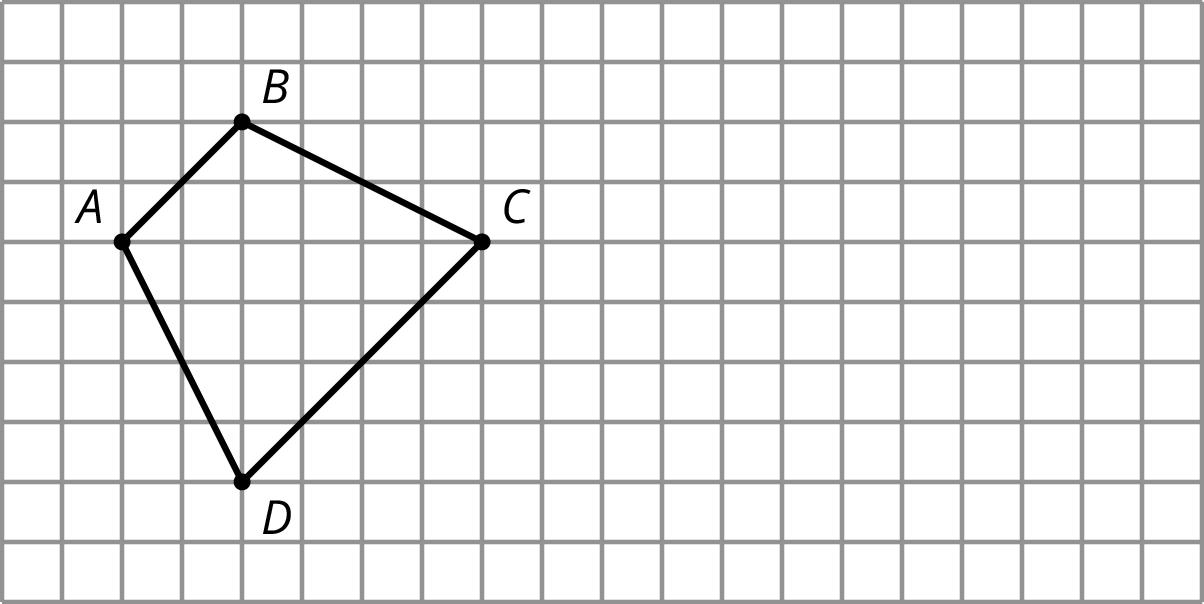
On the grid, draw a scaled copy of quadrilateral \(ABCD\) using a scale factor of \(\frac12\).