Lesson 10

Composing Figures

Let’s use reasoning about rigid transformations to find measurements without measuring.

Problem 1

Here is the design for the flag of Trinidad and Tobago.

The flag of Trinidad and Tobago: a red rectangle with a black stripe outlined with narrow white stripe from upper left corner to lower right corner.

Describe a sequence of translations, rotations, and reflections that take the lower left triangle to the upper right triangle.

Problem 2

Here is a picture of an older version of the flag of Great Britain. There is a rigid transformation that takes Triangle 1 to Triangle 2, another that takes Triangle 1 to Triangle 3, and another that takes Triangle 1 to Triangle 4.

An image of an older version of the flag of Great Britain.
  1. Measure the lengths of the sides in Triangles 1 and 2. What do you notice?
  2. What are the side lengths of Triangle 3? Explain how you know.
  3. Do all eight triangles in the flag have the same area? Explain how you know.

Problem 3

  1. Which of the lines in the picture is parallel to line \(\ell\)? Explain how you know.
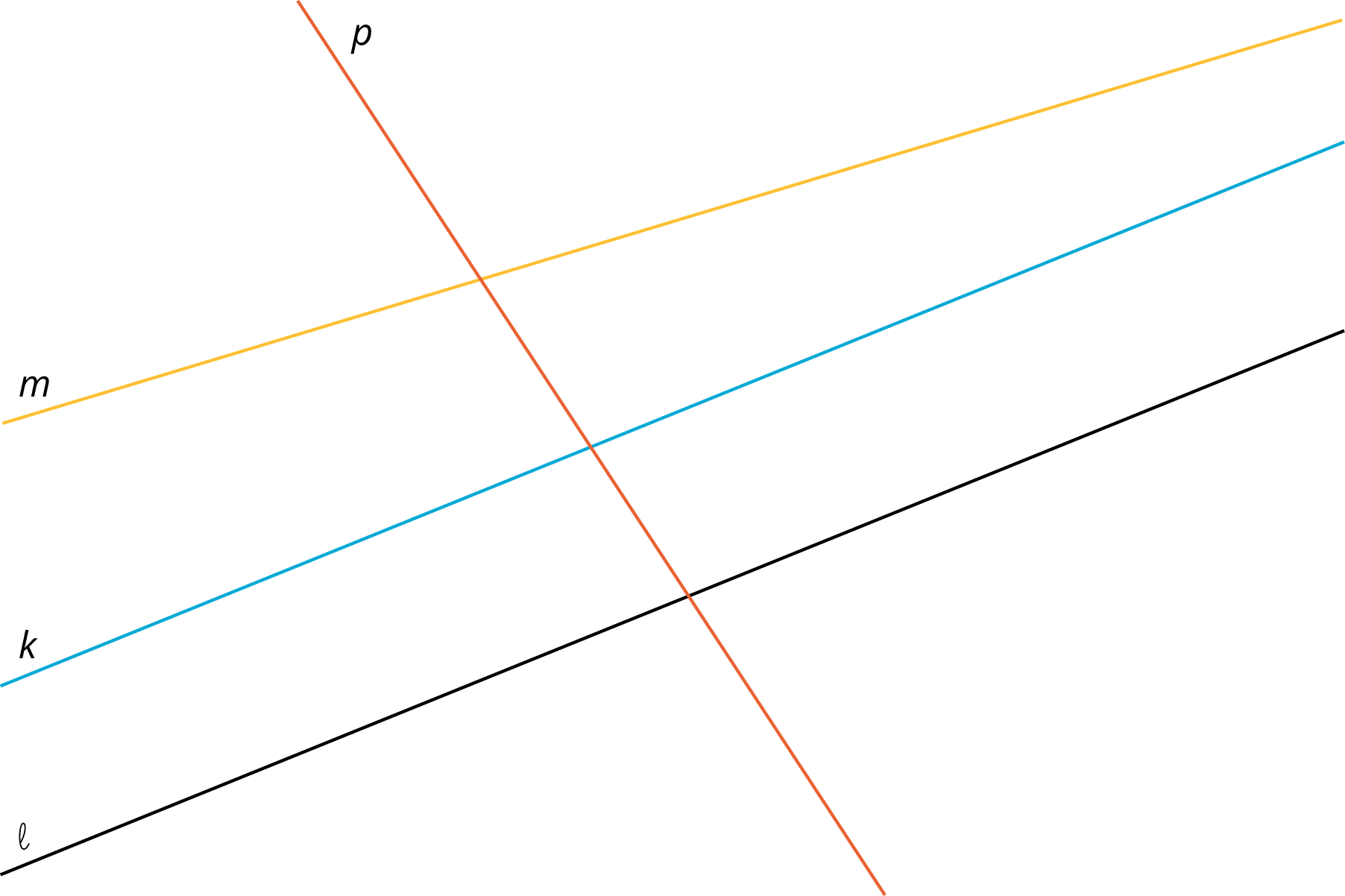
    Three lines, \(m, k \),  and \(l\), cut by a transversal, \(p\). 
  2. Explain how to translate, rotate or reflect line \(\ell\) to obtain line \(k\).
  3. Explain how to translate, rotate or reflect line \(\ell\) to obtain line \(p\).
(From Unit 1, Lesson 9.)

Problem 4

Point \(A\) has coordinates \((3,4)\). After a translation 4 units left, a reflection across the \(x\)-axis, and a translation 2 units down, what are the coordinates of the image?

(From Unit 1, Lesson 6.)

Problem 5

Here is triangle \(XYZ\):

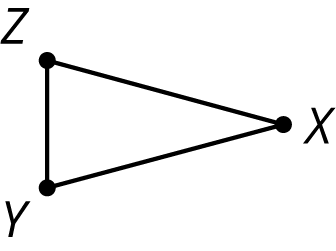
Triangle X Y Z appears isosceles, with Z Y vertical and Z X congruent to Y X.

 

Draw these three rotations of triangle \(XYZ\) together.

  1. Rotate triangle \(XYZ\) 90 degrees clockwise around \(Z\).
  2. Rotate triangle \(XYZ\) 180 degrees around \(Z\).
  3. Rotate triangle \(XYZ\) 270 degrees clockwise around \(Z\).
(From Unit 1, Lesson 8.)