Lesson 8
Position, Speed, and Direction
Let's use signed numbers to represent movement.
8.1: Distance, Rate, Time
- An airplane moves at a constant speed of 120 miles per hour for 3 hours. How far does it go?
- A train moves at constant speed and travels 6 miles in 4 minutes. What is its speed in miles per minute?
- A car moves at a constant speed of 50 miles per hour. How long does it take the car to go 200 miles?
8.2: Going Left, Going Right
- After each move, record your location in the table. Then write an expression to represent the ending position that uses the starting position, the speed, and the time. The first row is done for you.
starting
positiondirection speed
(units per
second)time
(seconds)ending
position
(units)expression 0 right 5 3 +15 \(0 + 5 \boldcdot 3\) 0 left 4 6 0 right 2 8 0 right 6 2 0 left 1.1 5 - How can you see the direction of movement in the expression?
- Using a starting position \(p\), a speed \(s\), and a time \(t\), write two expressions for an ending position. One expression should show the result of moving right, and one expression should show the result of moving left.
8.3: Velocity
A traffic safety engineer was studying travel patterns along a highway. She set up a camera and recorded the speed and direction of cars and trucks that passed by the camera. Positions to the east of the camera are positive, and to the west are negative.
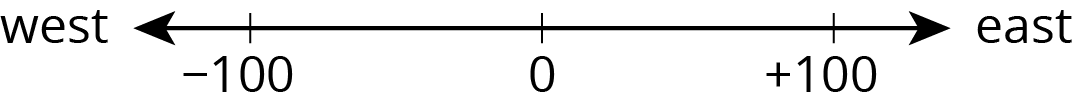
Vehicles that are traveling towards the east have a positive velocity, and vehicles that are traveling towards the west have a negative velocity.
- Complete the table with the position of each vehicle if the vehicle is traveling at a constant speed for the indicated time period. Then write an equation.
velocity
(meters per
second)time after passing
the camera
(seconds)ending
position
(meters)equation
describing
the position+25 +10 +250 \(25 \boldcdot 10 = 250\) -20 +30 +32 +40 -35 +20 +28 0 - If a car is traveling east when it passes the camera, will its position be positive or negative 60 seconds after it passes the camera? If we multiply two positive numbers, is the result positive or negative?
- If a car is traveling west when it passes the camera, will its position be positive or negative 60 seconds after it passes the camera? If we multiply a negative and a positive number, is the result positive or negative?
In many contexts we can interpret negative rates as "rates in the opposite direction." For example, a car that is traveling -35 miles per hour is traveling in the opposite direction of a car that is traveling 40 miles per hour.
- What could it mean if we say that water is flowing at a rate of -5 gallons per minute?
-
Make up another situation with a negative rate, and explain what it could mean.
Summary
We can use signed numbers to represent the position of an object along a line. We pick a point to be the reference point, and call it zero. Positions to the right of zero are positive. Positions to the left of zero are negative.
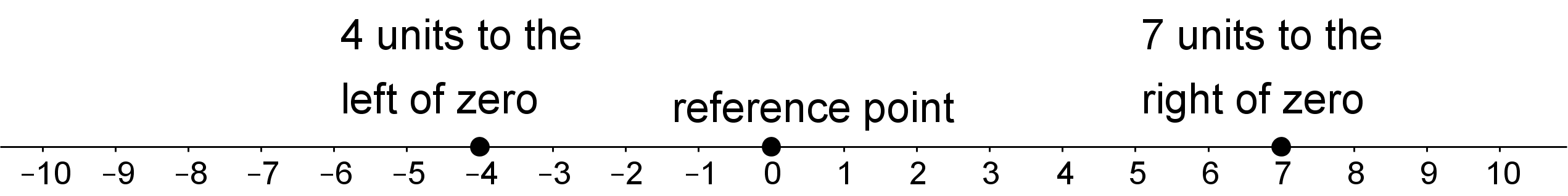
When we combine speed with direction indicated by the sign of the number, it is called velocity. For example, if you are moving 5 meters per second to the right, then your velocity is +5 meters per second. If you are moving 5 meters per second to the left, then your velocity is -5 meters per second.
If you start at zero and move 5 meters per second for 10 seconds, you will be \(5\boldcdot 10= 50\) meters to the right of zero. In other words, \( 5\boldcdot 10 = 50\).
If you start at zero and move -5 meters per second for 10 seconds, you will be \(5\boldcdot 10= 50\) meters to the left of zero. In other words,
\(\displaystyle \text-5\boldcdot 10 = \text-50\)
In general, a negative number times a positive number is a negative number.