Lesson 16
Representing Contexts with Equations
Let’s write equations that represent situations.
16.1: Don't Solve It
Is the solution positive or negative?
\((\text-8.7)(1.4) = a\)
\(\text- 8.7b = 1.4\)
\(\text-8.7 + c = \text- 1.4\)
\(\text-8.7 - d = \text- 1.4\)
16.2: Warmer or Colder than Before?
For each situation,
-
Find two equations that could represent the situation from the bank of equations. (Some equations will not be used.)
-
Explain what the variable \(v\) represents in the situation.
-
Determine the value of the variable that makes the equation true, and explain your reasoning.
Bank of equations:
| \(\text-3v=9\) | \(v = \text-16 + 6\) | \(v = \frac13 \boldcdot (\text-6)\) | \(v+12=4\) | \(\text-4\boldcdot 3=v\) |
| \(v = 4 + (\text-12)\) | \(v = \text-16 - (6)\) | \(v=9+3\) | \(\text-4 \boldcdot \text-3 = v\) | \(\text-3v = \text-6\) |
| \(\text-6 + v = \text-16\) | \(\text-4 = \frac13v\) | \(v=\text-\frac13 \boldcdot 9\) | \(v = \text-\frac13 \boldcdot (\text-6)\) | \(v = 4 + 12\) |
- Between 6 a.m. and noon, the temperature rose 12 degrees Fahrenheit to 4 degrees Fahrenheit.
- At midnight the temperature was -6 degrees. By 4 a.m. the temperature had fallen to -16 degrees.
- The temperature is 0 degrees at midnight and dropping 3 degrees per hour. The temperature is -6 degrees at a certain time.
- The temperature is 0 degrees at midnight and dropping 3 degrees per hour. The temperature is 9 degrees at a certain time.
- The temperature at 9 p.m. is one third the temperature at midnight.
You may use this applet if you find it helpful.
16.3: Animals Changing Altitudes
-
Match each situation with a diagram.
- A penguin is standing 3 feet above sea level and then dives down 10 feet. What is its depth?
- A dolphin is swimming 3 feet below sea level and then jumps up 10 feet. What is its height at the top of the jump?
- A sea turtle is swimming 3 feet below sea level and then dives down 10 feet. What is its depth?
- An eagle is flying 10 feet above sea level and then dives down to 3 feet above sea level. What was its change in altitude?
- A pelican is flying 10 feet above sea level and then dives down reaching 3 feet below sea level. What was its change in altitude?
- A shark is swimming 10 feet below sea level and then swims up reaching 3 feet below sea level. What was its change in depth?
- A penguin is standing 3 feet above sea level and then dives down 10 feet. What is its depth?
-
Next, write an equation to represent each animal's situation and answer the question. Be prepared to explain your reasoning.
Diagrams
A
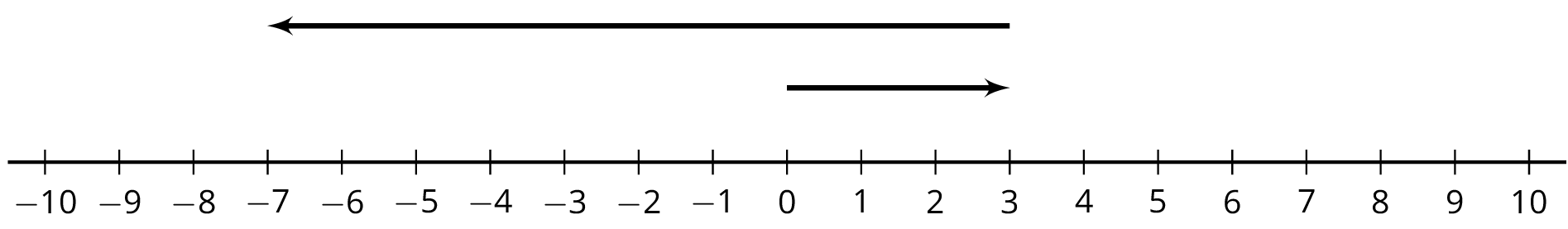
B

C
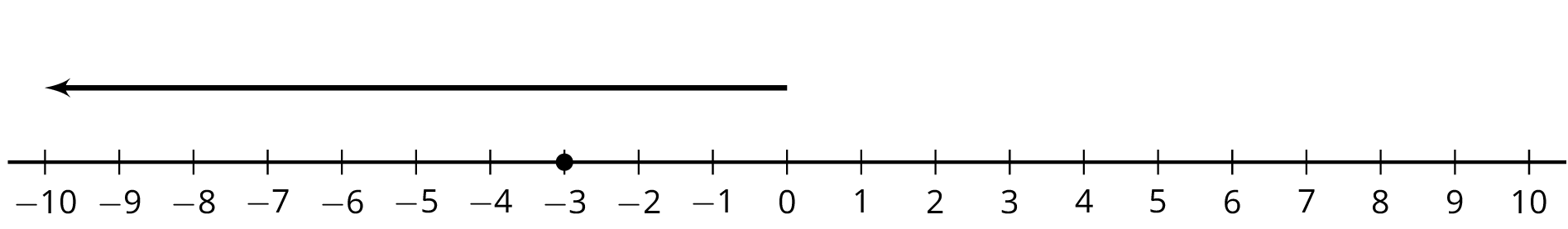
D
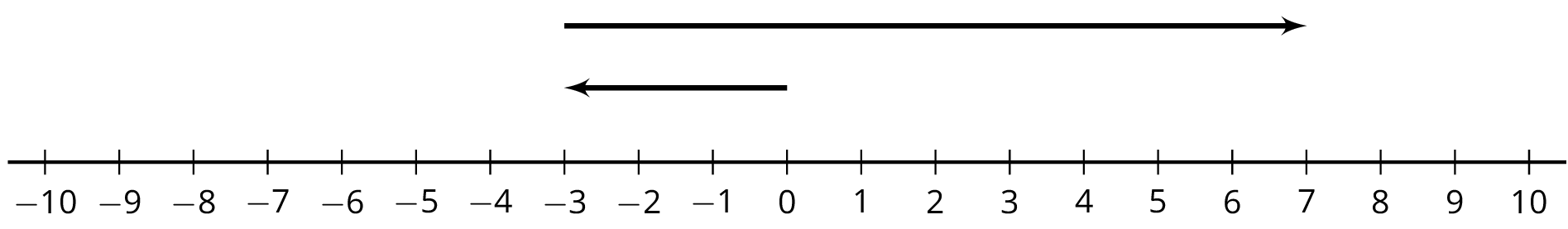
E
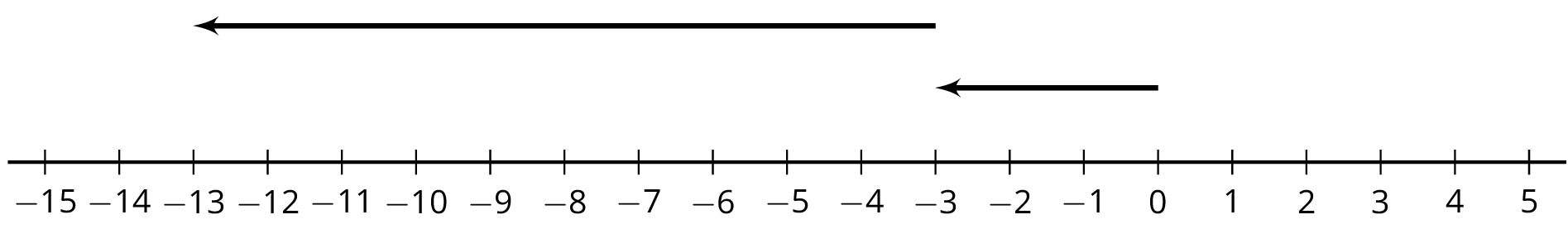
F
16.4: Equations Tell a Story
Your teacher will assign your group one of these situations. Create a visual display about your situation that includes:
-
An equation that represents your situation
-
What your variable and each term in the equation represent
-
How the operations in the equation represent the relationships in the story
-
How you use inverses to solve for the unknown quantity
-
The solution to your equation
-
As a \(7\frac14\) inch candle burns down, its height decreases \(\frac34\) inch each hour. How many hours does it take for the candle to burn completely?
-
On Monday \(\frac19\) of the enrolled students in a school were absent. There were 4,512 students present. How many students are enrolled at the school?
-
A hiker begins at sea level and descends 25 feet every minute. How long will it take to get to an elevation of -750 feet?
-
Jada practices the violin for the same amount of time every day. On Tuesday she practices for 35 minutes. How much does Jada practice in a week?
-
The temperature has been dropping \(2\frac12\) degrees every hour and the current temperature is \(\text-15 ^\circ\text{F}\). How many hours ago was the temperature \(0^\circ\text{F}\)?
-
The population of a school increased by 12%, and now the population is 476. What was the population before the increase?
-
During a 5% off sale, Diego pays $74.10 for a new hockey stick. What was the original price?
-
A store buys sweaters for $8 and sells them for $26. How many sweaters does the store need to sell to make a profit of $990?
Diego and Elena are 2 miles apart and begin walking towards each other. Diego walks at a rate of 3.7 miles per hour and Elena walks 4.3 miles per hour. While they are walking, Elena's dog runs back and forth between the two of them, at a rate of 6 miles per hour. Assuming the dog does not lose any time in turning around, how far has the dog run by the time Diego and Elena reach each other?
Summary
We can use variables and equations involving signed numbers to represent a story or answer questions about a situation.
For example, if the temperature is \(\text-3^\circ\text{C}\) and then falls to \(\text-17^\circ\text{C}\), we can let \(x\) represent the temperature change and write the equation:
\(\displaystyle \text-3 + x = \text- 17\)
We can solve the equation by adding 3 to each side. Since \(\text-17 + 3 = \text-14\), the change is \(\text-14^\circ\text{C}\).
Here is another example: if a starfish is descending by \(\frac32\) feet every hour then we can solve \(\displaystyle \text-\frac32h=\text-6\) to find out how many hours \(h\) it takes the starfish to go down 6 feet.
We can solve this equation by multiplying each side by \(\text-\frac23\). Since \(\text-\frac23\boldcdot \text-6 = 4\), we know it will take the starfish 4 hours to descend 6 feet.
Video Summary
Glossary Entries
- variable
A variable is a letter that represents a number. You can choose different numbers for the value of the variable.
For example, in the expression \(10-x\), the variable is \(x\). If the value of \(x\) is 3, then \(10-x=7\), because \(10-3=7\). If the value of \(x\) is 6, then \(10-x=4\), because \(10-6=4\).