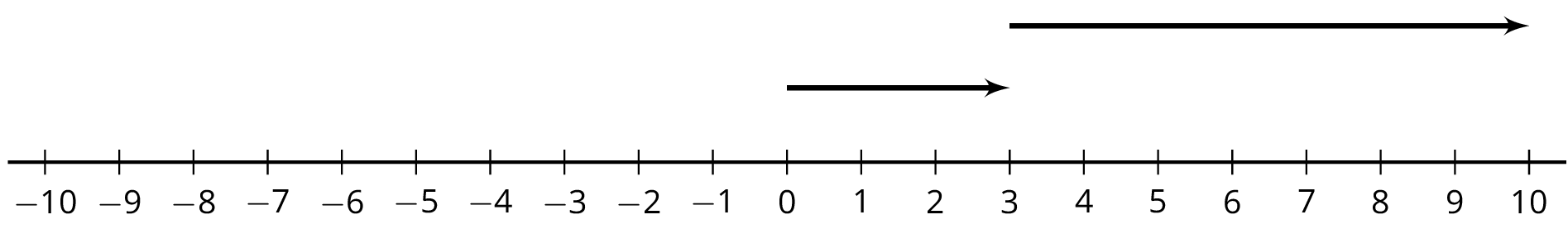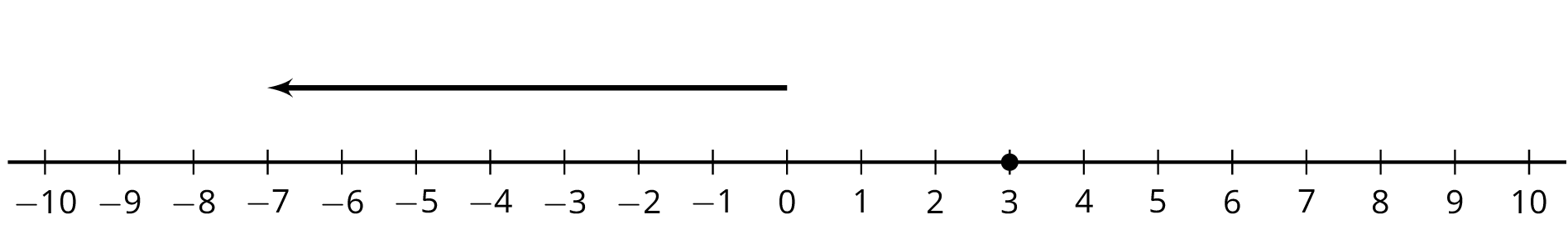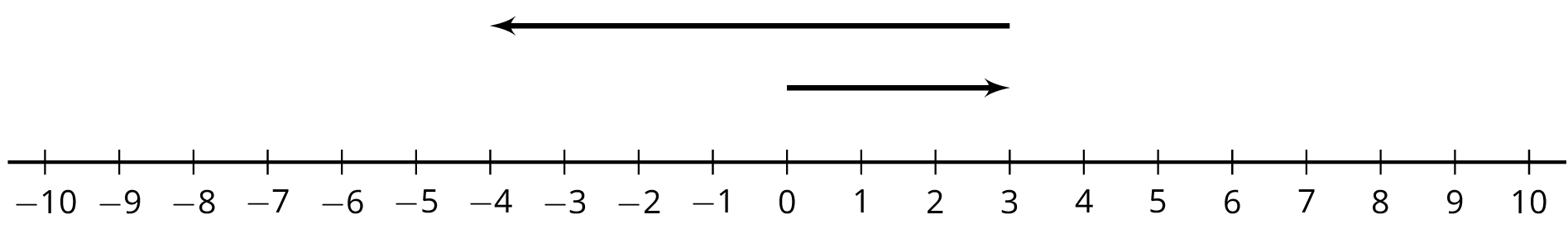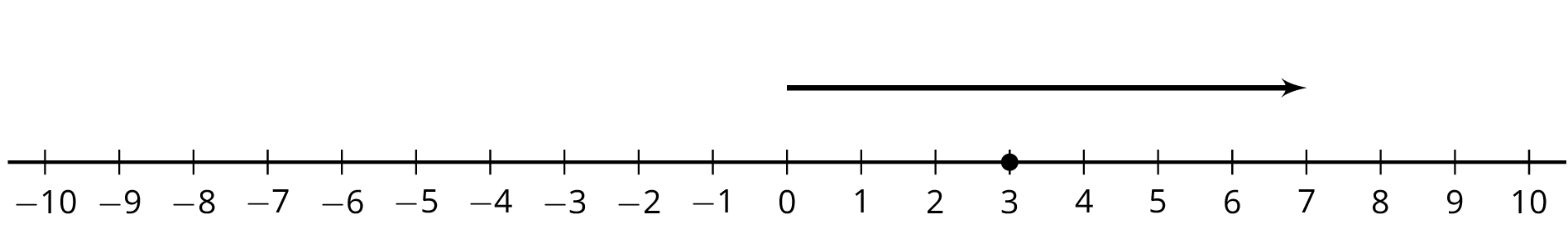Lesson 5
Representing Subtraction
Let's subtract signed numbers.
5.1: Equivalent Equations
Consider the equation \(2+3=5\). Here are some more equations, using the same numbers, that express the same relationship in a different way:
\(3 + 2 = 5\)
\(5 - 3 = 2\)
\(5 - 2 = 3\)
For each equation, write two more equations, using the same numbers, that express the same relationship in a different way.
- \(9+ (\text- 1)= 8\)
- \(\text- 11+ x= 7\)
5.2: Subtraction with Number Lines
-
Here is an unfinished number line diagram that represents a sum of 8.
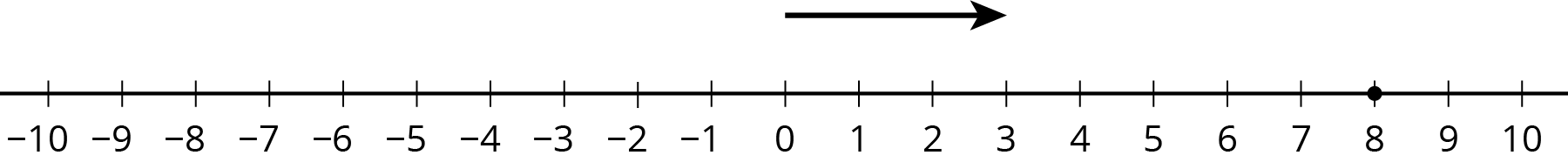
- How long should the other arrow be?
- For an equation that goes with this diagram, Mai writes \(3 + {?} = 8\).
Tyler writes \(8 - 3 = {?}\). Do you agree with either of them? - What is the unknown number? How do you know?
-
Here are two more unfinished diagrams that represent sums.
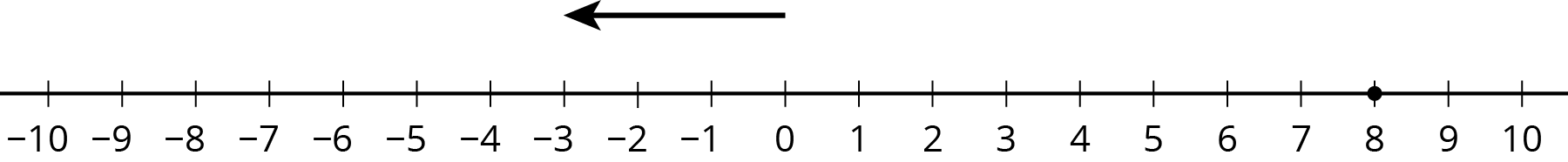
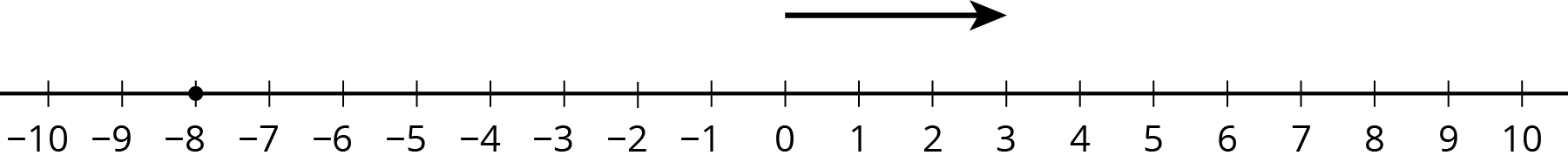
For each diagram:
- What equation would Mai write if she used the same reasoning as before?
- What equation would Tyler write if he used the same reasoning as before?
- How long should the other arrow be?
- What number would complete each equation? Be prepared to explain your reasoning.
- Draw a number line diagram for \((\text-8) - (\text-3) = {?}\) What is the unknown number? How do you know?
5.3: We Can Add Instead
-
Match each diagram to one of these expressions:
\(3 + 7\)
\(3 - 7\)
\(3 + (\text- 7)\)
\(3 - (\text- 7)\)
- Which expressions in the first question have the same value? What do you notice?
-
Complete each of these tables. What do you notice?
expression value \(8 + (\text- 8)\) \(8 - 8\) \(8 + (\text-5)\) \(8 - 5\) \(8 + (\text-12)\) \(8 - 12\) expression value \(\text-5 + 5\) \(\text-5 - (\text-5)\) \(\text-5 + 9\) \(\text-5 - (\text-9)\) \(\text-5 + 2\) \(\text-5 - (\text-2)\)
It is possible to make a new number system using only the numbers 0, 1, 2, and 3. We will write the symbols for adding and subtracting in this system like this: \(2 \oplus 1 = 3\) and \(2\ominus 1 = 1\). The table shows some of the sums.
| \(\oplus\) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 |
| 1 | 1 | 2 | 3 | 0 |
| 2 | 2 | 3 | 0 | 1 |
| 3 |
- In this system, \(1 \oplus 2 = 3\) and \(2 \oplus 3 = 1\). How can you see that in the table?
- What do you think \(3 \oplus 1\) should be?
- What about \(3\oplus 3\)?
- What do you think \(3\ominus 1\) should be?
- What about \(2\ominus 3\)?
- Can you think of any uses for this number system?
Summary
The equation \(7 - 5 = {?}\) is equivalent to \({?} + 5= 7\). The diagram illustrates the second equation.

Notice that the value of \(7 + (\text-5)\) is 2.

We can solve the equation \({?} + 5= 7\) by adding -5 to both sides. This shows that \(7 - 5= 7 + (\text- 5)\)
Likewise, \(3 - 5 = {?}\) is equivalent to \({?} + 5= 3\).

Notice that the value of \(3 + (\text-5)\) is -2.
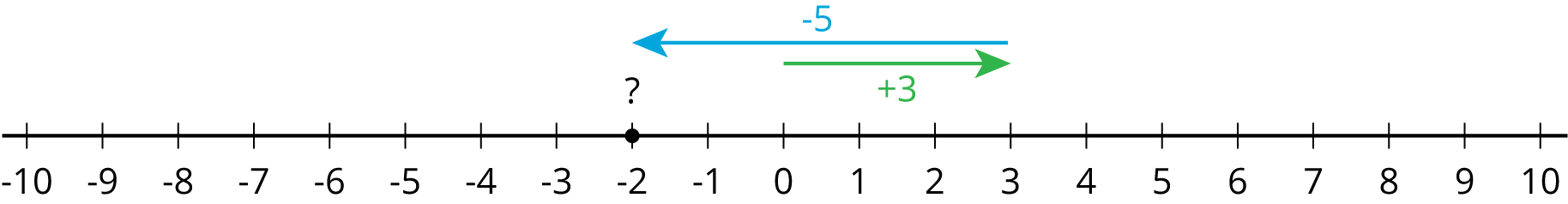
We can solve the equation \({?} + 5= 3\) by adding -5 to both sides. This shows that \(3 - 5 = 3 + (\text- 5)\)
In general:
\(\displaystyle a - b = a + (\text- b)\)
If \(a - b = x\), then \(x + b = a\). We can add \(\text- b\) to both sides of this second equation to get that \(x = a + (\text- b)\)
Glossary Entries
- deposit
When you put money into an account, it is called a deposit.
For example, a person added $60 to their bank account. Before the deposit, they had $435. After the deposit, they had $495, because \(435+60=495\).
- withdrawal
When you take money out of an account, it is called a withdrawal.
For example, a person removed $25 from their bank account. Before the withdrawal, they had $350. After the withdrawal, they had $325, because \(350-25=325\).