Lesson 9
Using the Partial Quotients Method
Let’s divide whole numbers.
Problem 1
Here is one way to find \(2,\!105 \div 5\) using partial quotients. Show a different way of using partial quotients to divide 2,105 by 5.
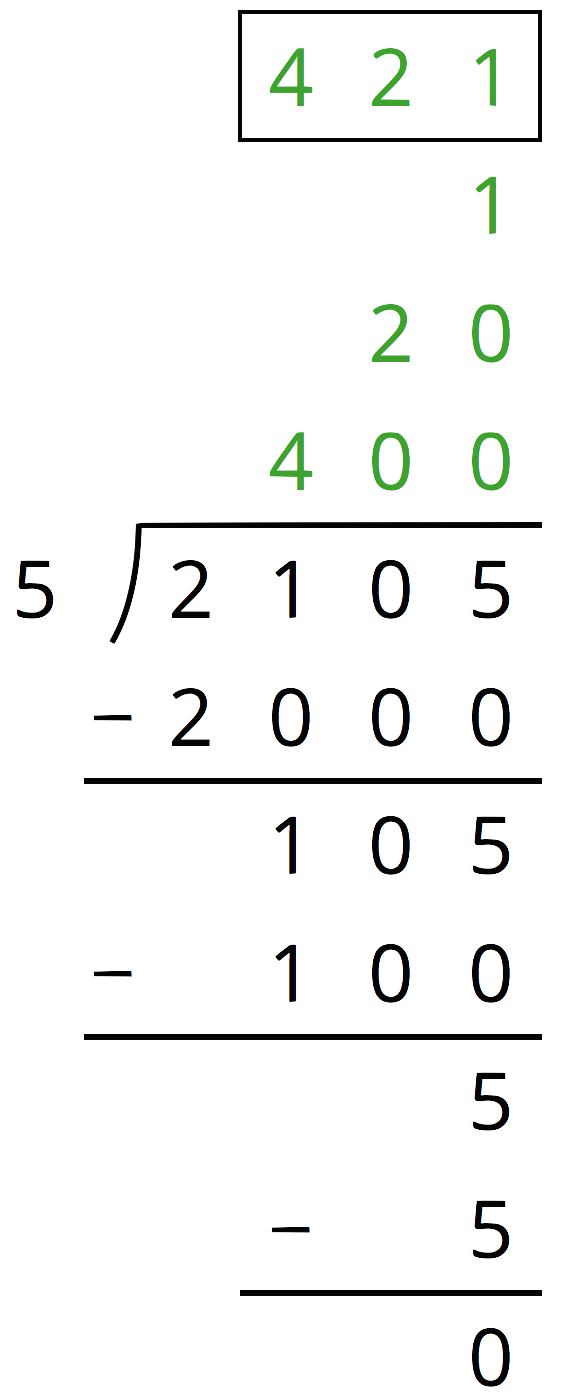
Problem 2

- How is Jada's work the same as Andre’s work? How is it different?
- Explain why they have the same answer.
Problem 3
Which might be a better way to evaluate \(1,\!150 \div 46\): drawing base-ten diagrams or using the partial quotients method? Explain your reasoning.
Problem 4
Here is an incomplete calculation of \(534\div 6\).
Write the missing numbers (marked with “?”) that would make the calculation complete.
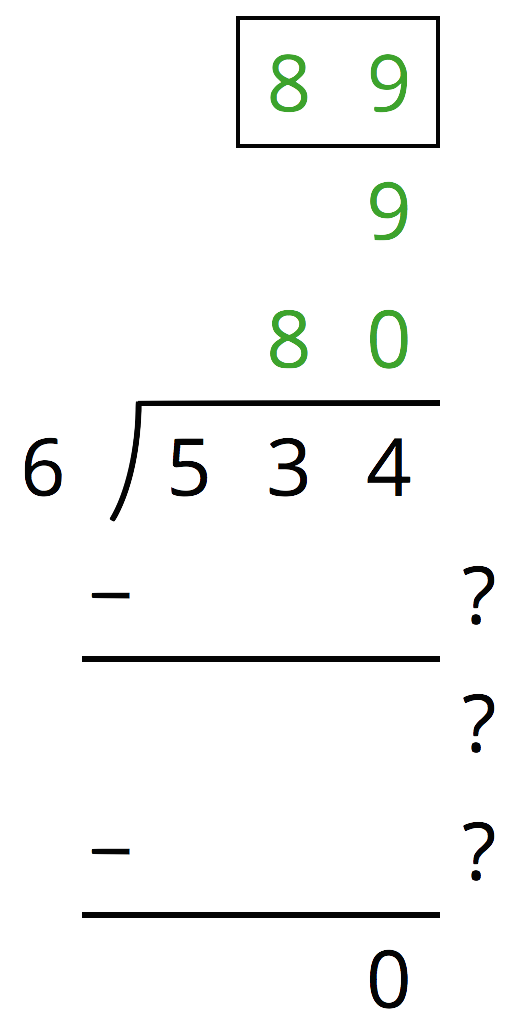
Problem 5
Use the partial quotients method to find \(1,\!032 \div 43\).
Problem 6
Which of the polygons has the greatest area?
A rectangle that is 3.25 inches wide and 6.1 inches long.
A square with side length of 4.6 inches.
A parallelogram with a base of 5.875 inches and a height of 3.5 inches.
A triangle with a base of 7.18 inches and a height of 5.4 inches.
Problem 7
One micrometer is a millionth of a meter. A certain spider web is 4 micrometers thick. A fiber in a shirt is 1 hundred-thousandth of a meter thick.
-
Which is wider, the spider web or the fiber? Explain your reasoning.
- How many meters wider?