Lesson 3

Adding and Subtracting Decimals with Few Non-Zero Digits

Let’s add and subtract decimals.

Problem 1

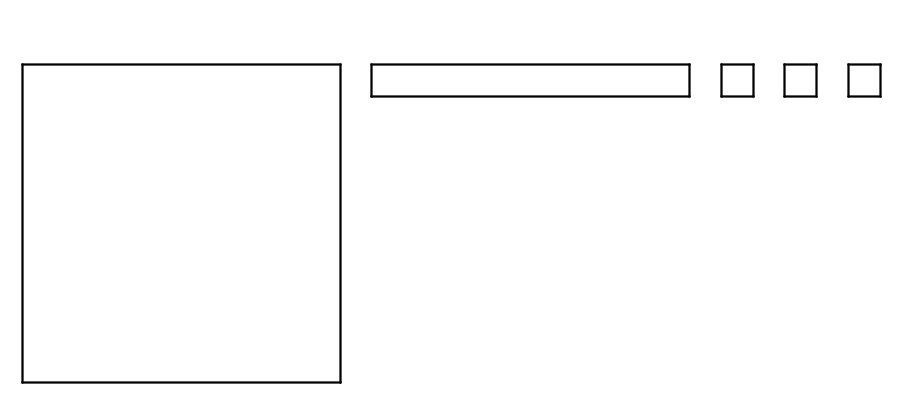
Here is a base-ten diagram that represents 1.13. Use the diagram to find \(1.13 - 0.46\).

Explain or show your reasoning.

A base-ten diagram representing 1 point 1 3. 1 large square, 1 rectangle, and 3 small squares. 

 

Problem 2

Compute the following sums. If you get stuck, consider drawing base-ten diagrams.

  1. \(0.027 + 0.004\)

  2. \(0.203 + 0.01\)

  3. \(1.2 + 0.145\)

Problem 3

A student said we cannot subtract 1.97 from 20 because 1.97 has two decimal digits and 20 has none. Do you agree with him? Explain or show your reasoning.

Problem 4

Decide which calculation shows the correct way to find \(0.3-0.006\) and explain your reasoning.

4 subtraction problems.

 

Problem 5

Complete the calculations so that each shows the correct difference.

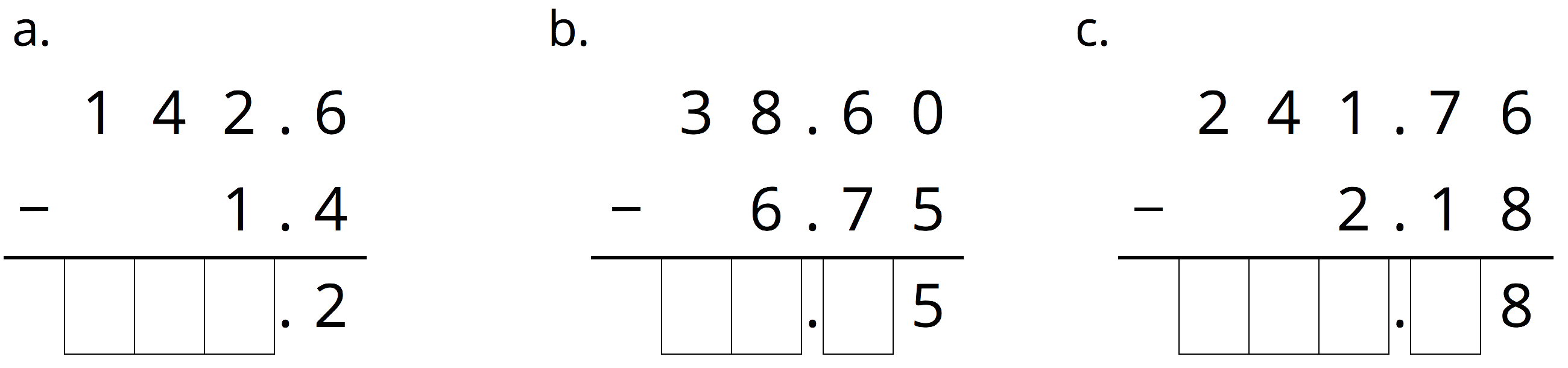
3 decimal subtraction problems. 

 

Problem 6

The school store sells pencils for $0.30 each, hats for $14.50 each, and binders for $3.20 each. Elena would like to buy 3 pencils, a hat, and 2 binders. She estimated that the cost will be less than $20.

  1. Do you agree with her estimate? Explain your reasoning.
  2. Estimate the number of pencils could she buy with $5. Explain or show your reasoning.
(From Unit 5, Lesson 1.)

Problem 7

A rectangular prism measures \(7\frac{1}{2}\) cm by 12 cm by \(15\frac{1}{2}\) cm.

  1. Calculate the number of cubes with edge length \(\frac{1}{2}\) cm that fit in this prism.
  2. What is the volume of the prism in \(\text{cm}^3\)? Show your reasoning. If you are stuck, think about how many cubes with \(\frac12\)-cm edge lengths fit into \(1\text{ cm}^3\).
(From Unit 4, Lesson 15.)

Problem 8

At a constant speed, a car travels 75 miles in 60 minutes. How far does the car travel in 18 minutes? If you get stuck, consider using the table.

minutes distance in miles
60 75
6
18
(From Unit 2, Lesson 12.)