Lesson 11

Dividing Numbers that Result in Decimals

Let’s find quotients that are not whole numbers.

Problem 1

Use long division to show that the fraction and decimal in each pair are equal.

\(\frac{3}{4}\) and 0.75

\(\frac{3}{50}\) and 0.06

\(\frac{7}{25}\) and 0.28

 

Problem 2

Mai walked \(\frac{1}{8}\) of a 30-mile walking trail. How many miles did Mai walk? Explain or show your reasoning.

Problem 3

Use long division to find each quotient. Write your answer as a decimal.

  1. \(99\div 12\)

  2. \(216 \div 5\)

  3. \(1,\!988 \div 8\)

Problem 4

Tyler reasoned: “\(\frac{9}{25}\) is equivalent to \(\frac{18}{50}\) and to \(\frac {36}{100}\), so the decimal of \(\frac{9}{25}\) is 0.36.”
 

  1. Use long division to show that Tyler is correct.

  2. Is the decimal of \(\frac{18}{50}\) also 0.36? Use long division to support your answer.

Problem 5

Complete the calculations so that each shows the correct difference.

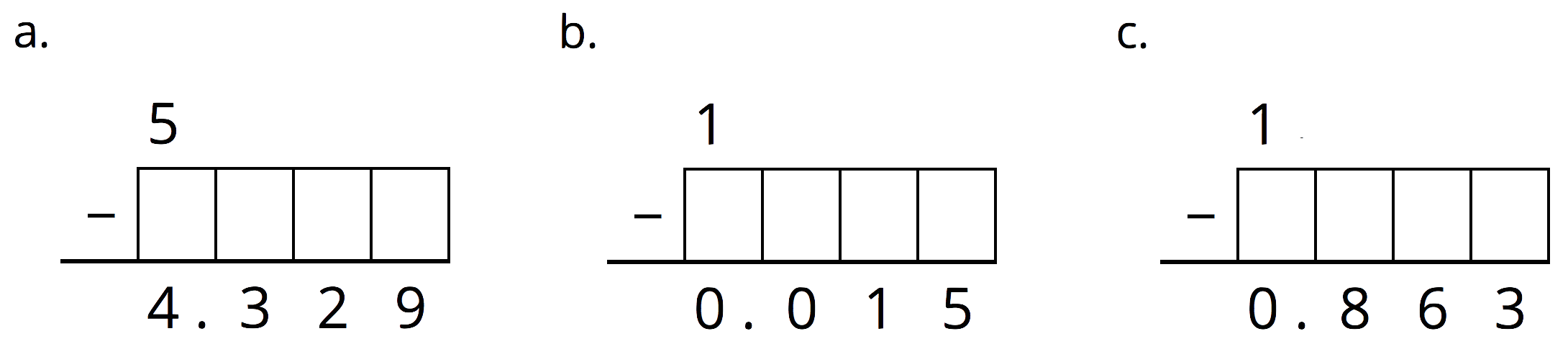
3 fill in the blank subtraction problems.
(From Unit 5, Lesson 4.)

Problem 6

Use the equation \(124 \boldcdot 15 = 1,\!860\) and what you know about fractions, decimals, and place value to explain how to place the decimal point when you compute \((1.24) \boldcdot (0.15)\).

(From Unit 5, Lesson 6.)