Lesson 8

Rising and Falling

View Student Lesson

Problem 1

A fan blade spins counterclockwise once per second.

Which of these graphs best depicts the height, \(h\), of \(P\) after \(s\) seconds? The fan blades are 1 foot long and the height is measured in feet from the center of the fan blades.

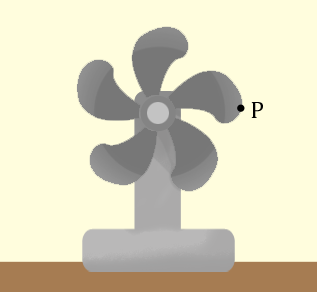
A drawing of a fan with 5 blades. The point P lies at the end of the blade directly to the right of the center of the fan.
A:
Coordinate plane, horizontal, s, 0 to 1, vertical, h, negative 1 to 1. Function oscillates from 0 comma 0 as high as 1, as low as negative 1, does 2 full cycles before ending at 1 comma 0.
B:
Coordinate plane, horizontal, s, 0 to 1, vertical, h, negative 1 to 1. Function oscillates from 0 comma 0 as low as negative 1, back up through point 5 comma 0, up as high as 1, down to 1 comma 0.
C:
Coordinate plane, horizontal, s, 0 to 1, vertical, h, negative 1 to 1. Function oscillates 0 comma 0, to negative 1, up to 1, back down to point 5 comma 0, then completes another cycle at 1 comma 0.
D:
Coordinate plane, horizontal, s, 0 to 1, vertical, h, negative 1 to 1. Function oscillates from 0 comma 0 as high as 1, back down through point 5 comma 0, down as low as negative 1, up to 1 comma 0.

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Which situations are modeled accurately by a periodic function? Select all that apply.

A:

the distance from the earth to the sun as a function of time

B:

the vertical height of a point on a rotating wheel as a function of time

C:

the area of a sheet of paper as a function of the number of times it is folded in half

D:

the number of centimeters in \(x\) inches

E:

the height of a swinging pendulum as a function of time

F:

the height of a ball tossed in the air as a function of time

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Here is the graph of a function for some values of \(x\).

Coordinate plane, x, negative 3 to 3 by 1, y, negative 0 to 5 by 1. A segment from 0 comma 1 to 1 comma 2.
  1. Can you extend the graph to the whole plane so that the function \(f\) is periodic? Explain your reasoning.
  2. Can you extend the graph to the whole plane so that the function \(f\) is not periodic? Explain your reasoning.

Solution

For access, consult one of our IM Certified Partners.

Problem 4

  1. Can a non-constant linear function be periodic? Explain your reasoning.
  2. Can a quadratic function be periodic? Explain your reasoning. 

Solution

For access, consult one of our IM Certified Partners.

Problem 5

Do \((7,1)\) and \((\text-5,5)\) lie on the same circle centered at \((0,0)\)? Explain how you know.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 6, Lesson 1.)

Problem 6

The measure of angle \(\theta\) is between 0 and \(2\pi\) radians. Which statements must be true of \(\sin(\theta)\) and \(\cos(\theta)\)? Select all that apply.

A:

\(\cos^2(\theta) + \sin^2(\theta) = 1\)

B:

If \(\sin(\theta) = 0\), then \(\cos(\theta) = 1\).

C:

If \(\sin(\theta) = 1\), then \(\cos(\theta) = 0\).

D:

\(\cos(\theta) + \sin(\theta) = 1\).

E:

The point \((\cos(\theta),\sin(\theta))\) lies on the unit circle.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 6, Lesson 5.)

Problem 7

The center of a clock is the origin \((0,0)\) in a coordinate system. The hour hand is 4 units long. What are the coordinates of the end of the hour hand at:

  1. 3:00
  2. 8:00
  3. 11:00

Solution

For access, consult one of our IM Certified Partners.

(From Unit 6, Lesson 7.)