Lesson 17
Comparing Transformations
17.1: Three Functions (5 minutes)
Warm-up
The purpose of this activity is for students to consider the graphs of three familiar types of functions, radical, linear, and quadratic, and understand that when the same transformations are applied to different function types, the graphs change in the same way. This warm-up also directly addresses that the order in which transformations are applied can matter, something which comes up repeatedly throughout the lesson.
Launch
Arrange students in groups of 2. Give students brief quiet work time followed by sharing their thinking with a partner.
Student Facing
For each pair of graphs, be prepared to describe a transformation from the graph on top to the graph on bottom.



Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students have difficulty identifying the transformations with precision, encourage them to try marking specific points on the graphs and considering how transformations take the point from one graph to the corresponding point on the other graph.
Activity Synthesis
There are many possible transformations that take the upper graph to the lower graph. Begin the discussion by displaying the three graphs and selecting students to share their transformation steps.
If the same set of steps is suggested for all three transformations, draw students' attention to them. Otherwise ask “What happens if we reflect the upper graph across the \(x\)-axis, and then translate it left 1 and down 3?” (That transformation works for all three.) Next, ask students if the transformation would work if we did the steps in a different order. (No, translating down and then reflecting across the \(x\)-axis has a different result than reflecting across the \(x\)-axis and then translating down.)
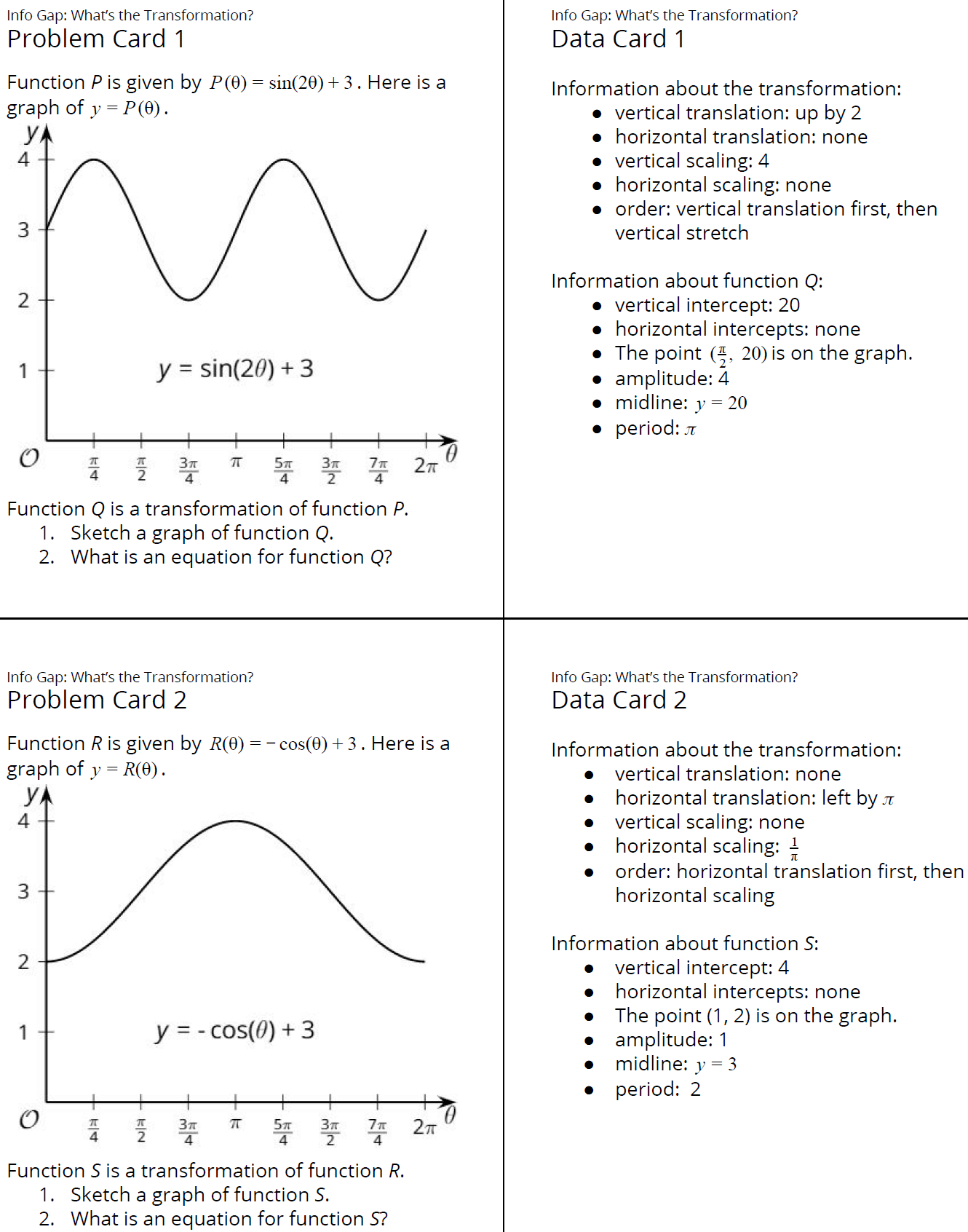
17.2: Info Gap: What's the Transformation? (25 minutes)
Activity
This info gap activity gives students an opportunity to determine and request the information needed to find and graph the transformation of a given function. In each case, the given function is a trigonometric function which has been translated horizontally or vertically and also reflected or scaled. The problem card gives the graph and equation of the trigonometric function. The student with the problem card figures out which transformations to apply to the graph and equation. The data cards give multiple ways for students to figure out the transformation. Monitor for students who
- ask for the explicit transformations and the order in which they are applied
- ask for the amplitude, midline, and period of the new function
The info gap structure requires students to make sense of problems by determining what information is necessary, and then to ask for information they need to solve it. This may take several rounds of discussion if their first requests do not yield the information they need (MP1). It also allows them to refine the language they use and ask increasingly more precise questions until they get the information they need (MP6).
Here is the text of the cards for reference and planning:
Launch
Tell students they will continue to work on identifying transformations between two functions. Explain the info gap structure, and consider demonstrating the protocol if students are unfamiliar with it.
Arrange students in groups of 2. In each group, distribute a problem card to one student and a data card to the other student. After you review their work on the first problem, give them the cards for a second problem and instruct them to switch roles.
Provide students with access to small sheets of graph paper.
Supports accessibility for: Memory; Organization
Design Principle(s): Cultivate Conversation
Student Facing
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the data card:
- Silently read the information on your card.
- Ask your partner “What specific information do you need?” and wait for your partner to ask for information. Only give information that is on your card. (Do not figure out anything for your partner!)
- Before telling your partner the information, ask “Why do you need to know (that piece of information)?”
- Read the problem card, and solve the problem independently.
- Share the data card, and discuss your reasoning.
If your teacher gives you the problem card:
- Silently read your card and think about what information you need to answer the question.
- Ask your partner for the specific information that you need.
- Explain to your partner how you are using the information to solve the problem.
- When you have enough information, share the problem card with your partner, and solve the problem independently.
- Read the data card, and discuss your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Suppose we considered the function \(T\) which is the sum of \(Q\) and \(S\). Is \(T\) also periodic? If yes, what is its period? If no, explain why not.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
After students have completed their work, share the correct answers and ask students to discuss the process of solving the problems. Focus on these points:
- The order of the transformations matters. For problem card 1, if the vertical stretch is done before the vertical translation it gives a different result, namely \(Q(x) = 4\sin(2x) + 14\). For problem card 2, if the horizontal stretch is done first and then the horizontal translation the result would be \(S(x) = \text-\cos(\pi (x + \pi))+3\)
- For the first card, the vertical translation will take \(\sin(2x) + 3\) to \(\sin(2x )+ 5\). For the vertical stretch, make sure students understand that both \(\sin(2x)\) and \(5\) need to be scaled by 4. The vertical stretch by 4 multiplies the output of the function by 4 and in this case the output, after the translation, is \(\sin(2x) + 5\).
- For the second card, the horizontal translation changes \(\text-\cos(x) + 3\) to \(\text-\cos(x+\pi) + 3\) and then the horizontal scaling by \(\frac{1}{\pi}\) gives \(\text-\cos(\pi x + \pi) + 3\). Unlike problem card 1, the scaling does not influence the constant 3 because the scale is horizontal while the 3 translated the graph vertically.
Ask students if they considered asking for the amplitude, period, and midline. In a sense, this information may be more straightforward to process because the order of the transformations is already encoded in this information. But the student with the problem card may not realize that this information is available.
Finally, ask students if they considered sketching the graph first and using this to find the transformed function. The sketch can help show major features of the graph (amplitude, midline, period) and serve as a guide for finding a valid equation.
17.3: Match the Graph (10 minutes)
Optional activity
This activity is optional. Use this activity to give students extra practice using technology to transform periodic functions.
The goal of this activity is for students to use graphing technology to transform the graph of a function to match another function. Because trigonometric functions are periodic, there are many ways to make the given transformations. Having the graphs allows students to use their visual intuition to visualize the transformations and then the main work of the activity is translating this into function notation.
Launch
Arrange students in groups of 2. Make sure each group has access to graphing technology.
Supports accessibility for: Language; Organization
Student Facing
Here is the graph of \(f(x)=\cos(x)\) and the graph of \(g\), which is a transformation of \(f\).

- Identify a transformation that takes \(f\) to \(g\) and write an equation for \(g\) in terms of \(f\) matching the transformation.
- Identify at least one other transformation that takes \(f\) to \(g\) and write an equation for \(g\) in terms of \(f\) matching the transformation.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The goal of this discussion is for students to make connections between the different ways to think about a graphical transformation and the different ways to algebraically rewrite an expression for a function.
Display the graphs of \(f\) and \(g\) for all to see. Invite groups to share their transformations, recording them alongside the graphs listing as many as students were able to identify. Here are some questions for discussion:
- “Why do \(g(x) = 2f\left(2(x-\frac{\pi}{4})\right)+3\) and \(g(x) = 2f\left(2x-\frac{\pi}{2}\right)+3\) both result in the same graph?” (The second is what happens if you use the distributive property. The value of the expression doesn't change, just the look.)
- “\(g(x)=\text-2f(2x+\frac{\pi}{2})+3\) works. How would you describe this transformation in words?” (Translate the graph of \(f\) left \(\frac{\pi}{2}\), stretch horizontally by a factor of \(\frac{1}{2}\), stretch vertically by a factor of 2, reflect over the \(x\)-axis, then translate up 3.)
Design Principle(s): Maximize meta-awareness; Cultivate conversation
Lesson Synthesis
Lesson Synthesis
The purpose of this discussion is for students to describe the graph of a transformation of a function in terms of the original function, calling back to the warm-up.
Arrange students in groups of 2–3 and display the table for all to see. Tell groups to be prepared to describe how to transform the graph of the original function to match the new function by only reading the equations and not doing any graphing. If time allows, have groups complete all 4 rows, otherwise assign groups 1–3 rows to complete.
| original function | new function | describe the transformation |
|---|---|---|
| \(A(x)= \cos(x)\) | \(B(x)= \text-\cos(x+1)\) | |
| \(C(x)= \sin(x)\) | \(D(x)= \sin(2x)-1\) | |
| \(F(x)= \cos(x)\) | \(G(x)= 3\cos{x-1}\) | |
| \(H(x)= \sin(x)\) | \(J(x)= \sin(2x+1) -5\) |
Select groups to share their descriptions, recording these for all to see (\(B\): translated left 1, reflected over the \(x\)-axis, \(D\): translated down 1, horizontal scaling by a factor of \(\frac{1}{2}\) (compressed), \(G\): vertical scaling by a factor of 3 (stretched), then translated down 1, \(J\): translated right 1 unit, then horizontal scaling by a factor of \(\frac{1}{2}\) (compressed), and translated down 5). In particular, if any groups wrote an equation for the new function in terms of the original, highlight their work as one strategy for making sense of transformations. For example, \(D(x)=C(2x)-1\). After groups give their descriptions, display the two graphs on the same axes so the class can check their thinking and revise where needed.
17.4: Cool-down - Follow the Moves (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Here are graphs of two trigonometric functions:

The function \(f\) is given by \(f(x) = \sin(x)\). How can we transform the graph of \(f\) to look like the graph of \(g\)? Looking at the graph of \(f\), we need to make the period and the amplitude smaller, translate the graph up, and translate the graph horizontally so it has a minimum at \(x=0\).
The amplitude of \(g\) is \(\frac{1}{2}\) and the period is \(\frac{\pi}{2}\) so we can begin by changing \(\sin(x)\) to \(\frac{1}{2}\sin(4x)\). The midline of \(g\) is 2.5 so we need a vertical translation of 2.5, giving us \(\frac{1}{2}\sin(4x)+2.5\). The function \(g\) has a minimum when \(x = 0\) while \(\frac{1}{2}\sin(4x)+2.5\) has a minimum when \(x = \text-\frac{ \pi}{8}\). So a horizontal translation to the right by \(\frac{\pi}{8}\) is needed. Putting all of this together, we have an expression for \(g\): \(g(x) = \frac{1}{2}\sin(4(x-\frac{\pi}{8}))+2.5\).
Another way to think about the transformation is to first notice that \(g\) has a minimum when \(x\) is 0. If we translate \(\sin(x)\) right by \(\frac{\pi}{2}\), then \(\sin(x-\frac{\pi}{2})\) also has a minimum at \(x=0\). The period of \(g\) is \(\frac{\pi}{2}\), so we can write \(\sin(4x-\frac{\pi}{2})\). The amplitude of \(g\) is \(\frac{1}{2}\) and it's midline is 2.5, so we end up with the expression \(\frac{1}{2} \sin(4x-\frac{\pi}{2})+2.5\) for \(g\). This is the same as \(g(x) = \frac{1}{2}\sin(4(x-\frac{\pi}{8}))+2.5\), just thinking of the horizontal translation and scaling in different orders.