Lesson 16

More Symmetry

View Student Lesson

Problem 1

For each figure, identify any angles of rotation that create symmetry.

A yin yang symbol.
A flag. A blue background with a white X.
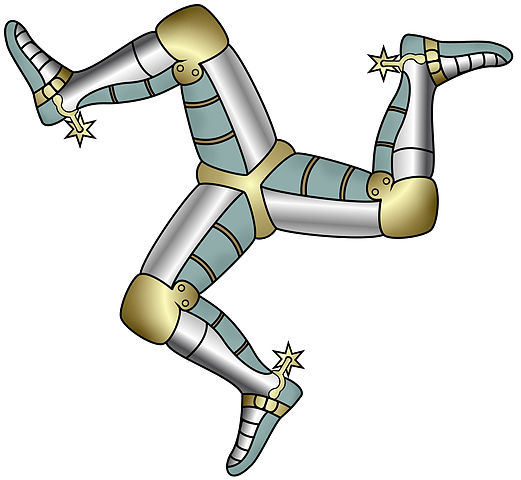
A triskelion image, three congruent legs radiating from a center point.

 

Solution

For access, consult one of our IM Certified Partners.

Problem 2

A triangle has rotation symmetry that can take any of its vertices to any of its other vertices. Select all conclusions that we can reach from this.

A:

All sides of the triangle have the same length.

B:

All angles of the triangle have the same measure.

C:

All rotations take one half of the triangle to the other half of the triangle.

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Select all the angles of rotation that produce symmetry for this flower.

Flower on polar grid.
A:

45 degrees

B:

90 degrees

C:

135 degrees

D:

180 degrees

E:

225 degrees

F:

270 degrees

Solution

For access, consult one of our IM Certified Partners.

Problem 4

Identify any lines of symmetry the figure has.

Two congruent circles on polar grid.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 15.)

Problem 5

A triangle has a line of symmetry. Select all conclusions that must be true.

A:

All sides of the triangle have the same length.

B:

All angles of the triangle have the same measure.

C:

No sides of the triangle have the same length.

D:

No angles of the triangle have the same measure.

E:

Two sides of the triangle have the same length.

F:

Two angles of the triangle have the same measure.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 15.)

Problem 6

Here are 4 triangles that have each been transformed by a different transformation. Which transformation is not a rigid transformation?

A:
Two triangles, ABC and A prime B prime C prime.
B:
Two triangles, A B C and A prime B prime C prime.
C:
Two triangles, A B C and A prime B prime C prime.
D:
Two triangles, A B C and A prime B prime C prime.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 10.)

Problem 7

Match each directed line segment with the translation from Polygon \(P\) to Polygon \(Q\) by that directed line segment.

Translation 1

Congruent triangles. Triangle Q, translated down and to the right of Triangle P.

Translation 2

Congruent triangles. Triangle P, translated up and to the right of Triangle Q.

Translation 3

Congruent triangles overlapping. Triangle Q, below and to the left of Triangle P. Triangle Q overlaps the bottom of Triangle P.

Translation 4

Congruent triangles. Triangle P, below and to the right of Triangle Q.
A:
A directed line segment, v, slants upward and to the left. Endpoint on bottom end, arrow at top end touching a point.
B:
A directed line segment, a, slants downward and to the left. Endpoint on top end, arrow at bottom end touching a point.
C:
A directed line segment, u, slants downward and slightly to the left. Endpoint on top end, arrow at bottom end touching a point.
D:
A directed line segment, w, slants downward and to the right. Endpoint on top end, arrow at bottom end touching a point.

 

1:

Translation 1

2:

Translation 2

3:

Translation 3

4:

Translation 4

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 12.)