Lesson 6
Analyzing Graphs
6.1: Fractions and Decimals (5 minutes)
Warm-up
This warm-up encourages students to look for patterns in real numbers, namely the decimal expansions of powers of \(\frac{1}{2}\). Students are likely to recognize the 5, 25, 125 in the decimal expansion as powers of 5, and use that insight to describe the pattern, extend it, and to notice other related patterns. In this Warm-up, they are not expected to reason about why the non-zero digits of the decimal expansions of powers of \(\frac12\) are related to powers of 5.
Launch
Arrange students in groups of 2. Encourage them to think quietly for a minute before sharing their responses with their partner.
Student Facing
| fraction | \(\frac12\) | \(\frac14\) | \(\frac18\) | \(\frac{1}{16}\) | \(\frac{1}{32}\) |
|---|---|---|---|---|---|
| decimal | 0.5 | 0.25 | 0.125 |
In the table, find as many patterns as you can. Use one or more patterns to help you complete the table. Be prepared to explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select a few students (or groups) to share their responses. If not already mentioned by students, discuss:
- “Are the successive numbers exhibiting linear or exponential change? How do you know?”
- “Are the successive numbers getting larger or smaller? How do you know?”
If time permits, consider asking: “Why do powers of 5 show up in the decimals?”
6.2: Falling and Falling (15 minutes)
Activity
Students analyze graphs representing the depreciation of the values of two cell phones. The value of a new cell phone tends to be highest at its initial release and falls over time. Some phones depreciate in a roughly exponential fashion.
Students also write equations to represent the relationship between time and value for each cell phone. To represent the relationships with equations, students need to know the initial value of each phone (which can be read from the graph) and the growth factor (which must be calculated).
Students may conclude that Phone A is decreasing in value more quickly than Phone B by comparing the graphs visually. They may also reason in one of the following ways:
- For Phone A, the annual differences in value are 400, 240, and 144 for the first few years. For Phone B, the annual differences are 210, 157.5, and 118.12. The differences for phone A are greater than the differences for phone B.
- Phone A loses \(\frac{2}{5}\) of its value each year while Phone B loses \(\frac{1}{4}\) of its value, so the value of Phone A is decreasing more quickly.
For quantities that change exponentially, the second way of reasoning is more appropriate (the former is suitable for quantities changing linearly). If the starting price of Phone B had been substantially higher than the starting price of Phone A, then Phone B would, at least at the beginning, have higher annual differences even if it is losing a smaller fraction of its value each year.
Launch
To give students an overview of the context, consider sharing a news clip or advertisement on the latest release of a popular cell phone, or asking students to share what they know about the latest models of some phones. Solicit ideas from students about how they think the value of a phone changes after it is released.
Students are likely to be familiar with the idea that phones decrease in value over time (especially as newer ones come along). Give an example of how a popular phone might have cost, for instance, $400 when it was first available to the public, but the same type of phone (in new condition) might cost several hundred dollars less a couple of years later. Remind students of the meaning of the word depreciate or depreciation, which should be familiar from a previous lesson about the value of a car.
Supports accessibility for: Conceptual processing; Memory
Student Facing
The value of some cell phones changes exponentially after initial release. Here are graphs showing the depreciation of two phones 1, 2, and 3 years after they were released.
Phone A

Phone B

- Which phone is more expensive to buy when it is first released?
- How does the value of each phone change with every passing year?
- Which one is falling in value more quickly? Explain or show how you know.
- If the phones continue to depreciate by the same factor each year, what will the value of each phone be 4 years after its initial release?
- For each cell phone, write an equation that relates the value of the phone in dollars to the years since release, \(t.\) Use \(v\) for the value of Phone A and \(w\) for the value of Phone B.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
When given data, it is not always clear how to best model it. In this case we were told the value of the cell phones was changing exponentially. Suppose, however, we were instead just given the initial values of the the cell phones when released and the values after each of the first three years.
- Use technology to compute the best fit line for each cell phone. Round any numbers to the nearest dollar.
- Explain why, in this situation, an exponential model might be more appropriate than the linear model you just created.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may not see, especially for the second graph, that the relationship is exponential. Ask them by what factor the value of each phone decreases in the first year. What about in the second year? Ask them what these numbers tell them about the growth factor.
Activity Synthesis
Invite students to share their responses. Focus the conversation on how they determined which phone loses value more quickly and how they wrote the equations.
Make sure students recognize that, to tell which phone depreciates more quickly, we need to identify a growth factor and cannot simply find the differences between consecutive values. Instead of subtracting, we should be dividing the value of one year by that of the previous year. Once the initial amount and the growth factor are identified, we can write an equation to predict the value of the phone later in time (assuming the mathematical model still applies, e.g., the technology is not considered obsolete or the phone doesn’t somehow become more valuable because of other extraneous reasons).
Design Principle(s): Support sense-making
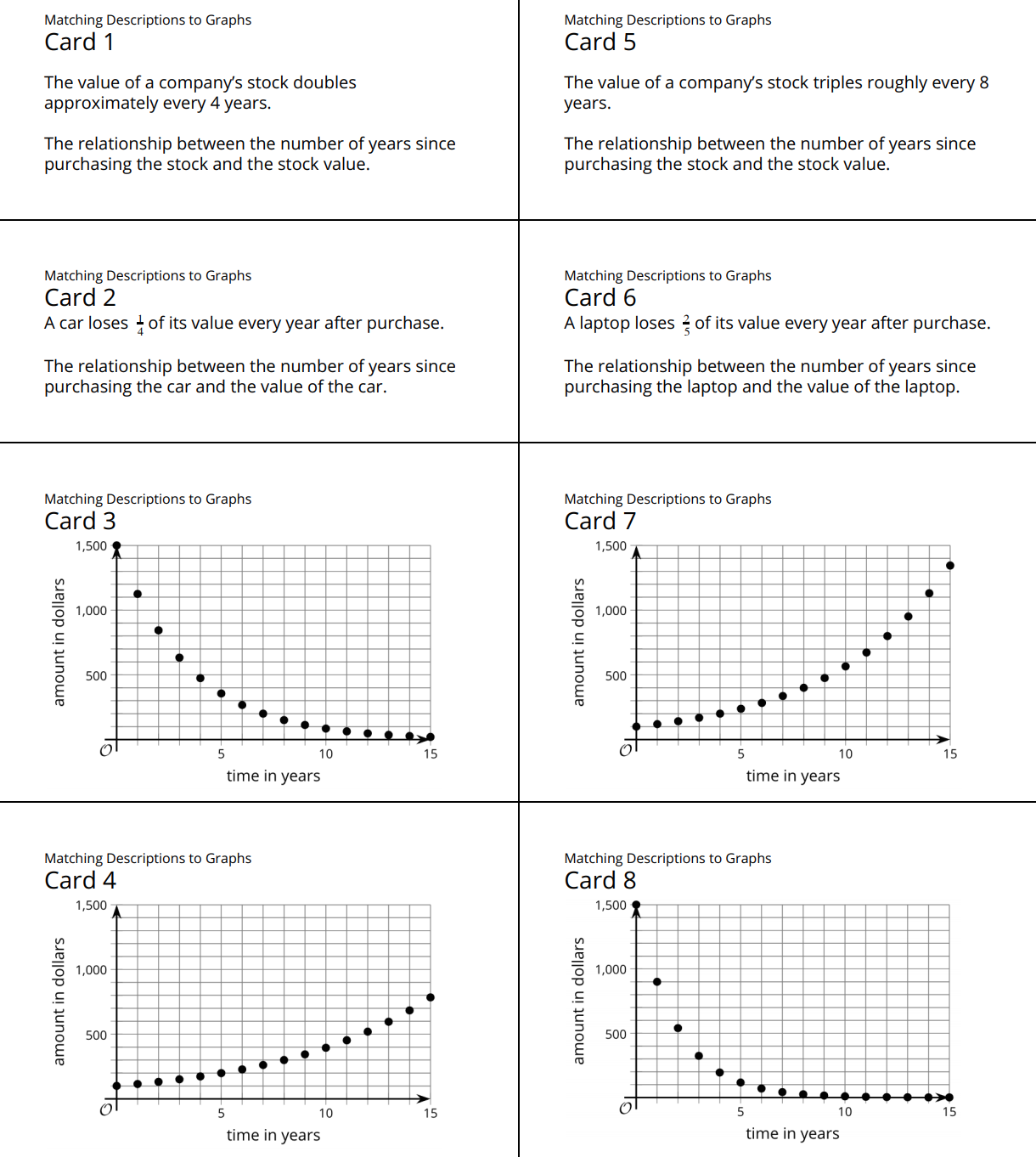
6.3: Card Sort: Matching Descriptions to Graphs (15 minutes)
Activity
In this activity, students match four descriptions of situations characterized by exponential change with four graphs. In order to make a correct match, students will need to attend to whether the growth factor is greater than 1 or less than 1, and determine the growth factor from the graph with enough precision to distinguish between two possibilities.
Here are some strategies students may use to match. Look for students using these or other approaches so they could share later.
- Separate the cards and descriptions into situations that grow or decay, and then analyze the graphs more closely to compare their growth factors.
- Use the information in the descriptions to draw conclusions about the coordinates of points on the graphs.
Here are images of the cards for reference and planning:
Launch
Arrange students in groups of 2. Give each group a set of slips or cards from the Blackline Master. Ask students to take turns. The first partner identifies a match and explains why they think it is a match, while the other listens and works to understand. Then they switch roles. Before students begin working, demonstrate this routine if necessary.
Design Principle(s): Support sense-making; Maximize meta-awareness
Student Facing
Your teacher will give you a set of cards containing descriptions of situations and graphs. Match each situation with a graph that represents it. Record your matches and be prepared to explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students struggle to identify the correct graphs, ask them to look carefully at the scales. What do they notice? Once they see that the scales are the same, ask them how the graphs compare. Which one grows or decays faster? Then ask them which of the description cards represent growth and which represent decay. Which situation grows (or decays) faster?
Activity Synthesis
Select students to share their strategies, starting with the cards that suggest a growth factor that is greater than 1 (Card 1 and Card 5) and then moving to cards that suggest a growth factor that is positive and less than 1 (Card 2 and Card 6). If not mentioned by students, discuss questions such as:
- Can we use the vertical intercepts to make a match? (No, that information is not given in the descriptions of the situations. In the descriptions of situations with exponential decay, although a car is likely to cost more than a laptop, a used car might cost less than a new high-end laptop, so we can't be sure.)
- What can we tell about the growth factor in each situation? (The growth happens more quickly for the situation in Card 1 than in Card 5 because that stock quadruples every eight years. For cards 2 and 6, the phone loses \(\frac25\) of its value every year, while the car only loses \(\frac14\) of its value each year.)
Supports accessibility for: Language; Organization
Lesson Synthesis
Lesson Synthesis
Review how we can gather key information about situations from graphs representing them. Display one graph from the lesson, and ask:
- “How can you use the graph to determine the initial amount?”
- “How can you tell whether the growth factor is greater than 1 or less than 1?”
- “How can you use the graph to determine the growth factor?”
- “Once you know the initial amount and the growth factor, how can you construct an equation to represent the relationship?”
6.4: Cool-down - A Phone, a Company, a Camera (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Graphs are useful for comparing relationships. Here are two graphs representing the amount of caffeine in Person A and Person B, in milligrams, at different times, measured hourly, after an initial measurement.
A

B

The graphs reveal interesting information about the caffeine in each person over time:
- At the initial measurement, Person A has more caffeine (200 milligrams) than Person B (100 milligrams).
- The caffeine in Person A's body decreases faster. It went from 200 to 160 milligrams in an hour. Because 160 is \(\frac{8}{10}\) or \(\frac45\) of 200, the growth factor is \(\frac45\).
- The caffeine in Person B's body went from 100 to about 90 milligrams, so that growth factor is about \(\frac{9}{10}\). This means that after each hour, a larger fraction of caffeine stays in Person B than in Person A.
- Even though Person A started out with twice as much caffeine, because of the growth factor, Person A had less caffeine than Person B after 6 hours.