Lesson 16
Compounding Interest
16.1: Five Years Later (5 minutes)
Warm-up
In this warm-up, students practice writing an exponential expression for repeated interest calculations. To emphasize the exponential structure of compounded interest, they are prompted to write an expression before calculating a monetary value.
Student Facing
You owe 12% interest each year on a $500 loan. If you make no payments and take no additional loans, what will the loan balance be after 5 years?
Write an expression to represent the balance and evaluate it to find the answer in dollars.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may find it difficult to write an expression because they are reasoning about the interest calculation in additive terms, for example, \(500 + (0.12) \boldcdot500\) for the first year, \([500 + (0.12) \boldcdot500] + (0.12) \boldcdot[500 + (0.12) \boldcdot500] \) for the second year, and so on. Encourage them to think about each year's calculation as a product and to refer to the work in a previous lesson, if needed.
Activity Synthesis
Invite students to share their expressions. If not already brought up in students' responses, bring up the following two expressions:
- \(500 \boldcdot (1.12) \boldcdot (1.12) \boldcdot (1.12) \boldcdot (1.12) \boldcdot (1.12)\)
- \(500 \boldcdot (1.12)^5\)
Highlight that the first expression with the 1.12 written out five times makes explicit the five separate years over which the interest is compounded. The second expression is shorthand for the first and is more succinct.
16.2: Resizing Images (10 minutes)
Activity
In this activity, students use a geometric context to investigate whether increasing an amount by 10% and then increasing the result by 10% again is the same as applying 20% increase once. The work addresses a common misconception about successive percent increase. While the two increases (10% twice and 20% once) are in fact relatively close in value, they are not identical. The difference will become more pronounced the more times that the percent increase is applied.
The work prepares students to see how banks and credit card companies actually calculate or compound interest, which is explored in upcoming activities. Rather than charging customers with interest on an annual basis, they calculate and compound the interest on a daily or monthly basis, which typically results in a different actual rate for one year than the published annual interest rate.
The same principle applies for repeated percent decrease, i.e., the result of decreasing by 10% three successive times is not the same as decreasing it by 30% once. Recall that earlier in the unit, students have seen that a car losing \(\frac13\) of its value in any given year (a varying amount) is not the same as losing \(\frac13\) of its original value every year (a fixed amount).
As students work, monitor for those who use the following strategies so they can share later.
- Choose a number for the height, apply each method of scaling, then compare the two resulting heights.
- Compare the scale factors for the two methods (i.e. think in terms of multiplying the height by \((1.1)^2\) for Andre's method and by 1.2 for Mai's method).
- Use a variable for the height, apply each method of scaling, and then compare the resulting expressions.
Launch
Arrange students in groups of 2. Give students 1–2 minutes of quiet think time and a minute to discuss their response with their partner. Follow with a whole-class discussion.
Design Principle(s): Support sense-making
Supports accessibility for: Visual-spatial processing; Conceptual processing
Student Facing
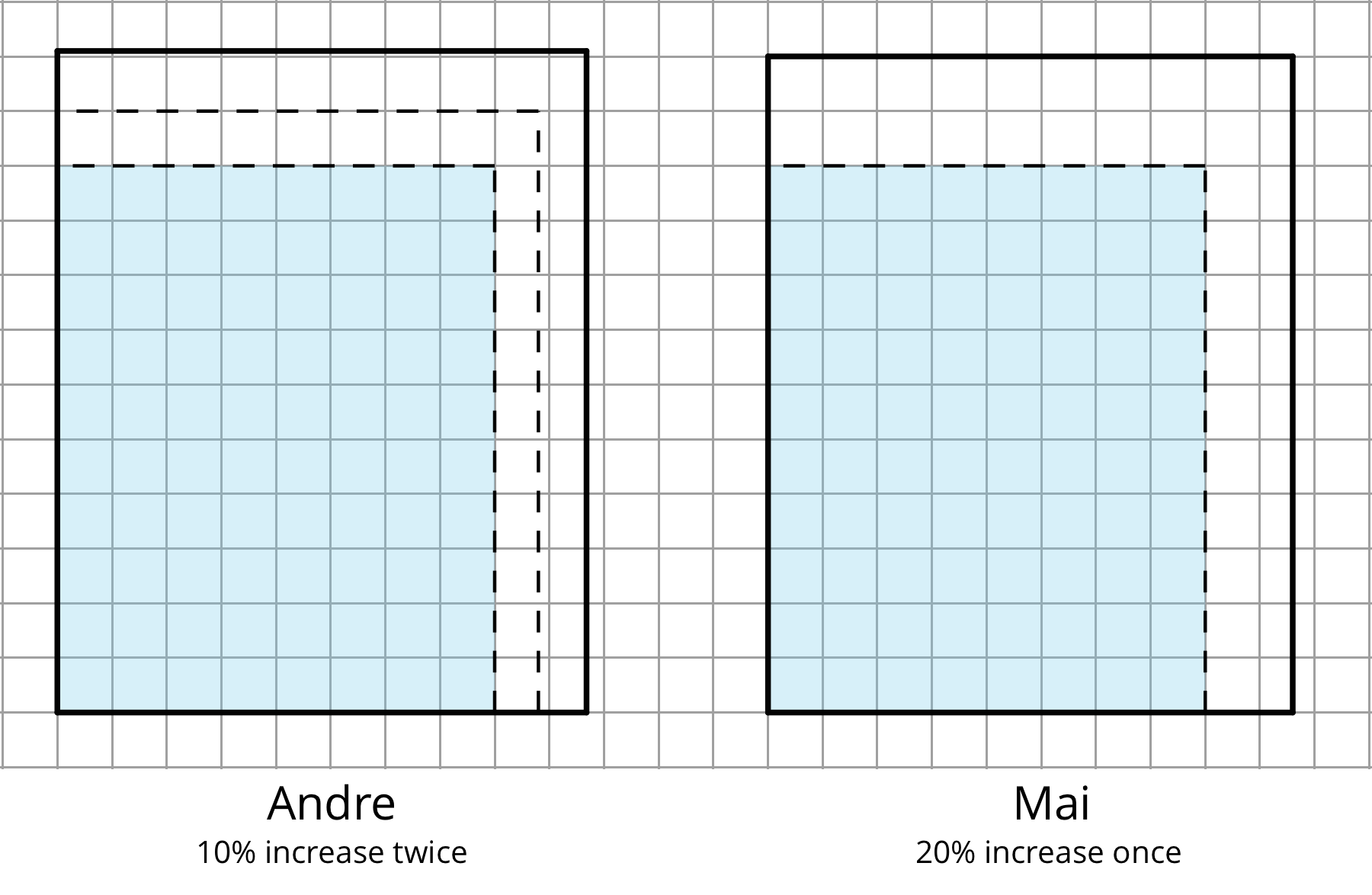
Andre and Mai need to enlarge two images for a group project. The two images are the same size.
Andre makes a scaled copy of his image, increasing the lengths by 10%. It was still a little too small, so he increases the lengths by 10% again.
Mai says, “If I scale my image and increase the lengths by 20%, our images will be exactly the same size.”
Do you agree with Mai? Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Adding 0.01 to a number 10 times is different from multiplying that number by 1.01 ten times, but the values you get from expressions like these are still quite close to one another. For example, \(5+(0.01)\boldcdot 10=5.1\) whereas \(5\boldcdot (1.01)^{10}\approx 5.523\). The first of these you could do in your head, whereas the second one would probably require a calculator, and so this introduces a neat mental math strategy.
- The quantity \((1.02)^7\) is hard to calculate by hand. Use mental math to compute \(1+(0.02)\boldcdot7\) to get a good approximation to it.
- Estimate \((0.99)^9\). Use a calculator to compare your estimate to the actual value.
- Estimate \((1.6)^{11}\). Use a calculator to compare your estimate to the actual value. What is different about this example?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may struggle to understand how to begin the problem. Although the general case is the intention, some students may benefit from having a concrete value for the original image. Suggest students begin with images that were 100 pixels tall and try additional starting values until a pattern is evident.
Activity Synthesis
Select previously identified students to share their strategies for comparing the two scaling methods. Use the same sequence as shown in possible responses starting with a concrete example (a numerical value for the height) and then moving toward a generalized case (using a variable).
If time permits, consider showing the following image to help students connect the symbolic work to a visual representation of Andre and Mai's approaches. The shaded area is the original image. The difference in height is slight but noticeable given the grid.
16.3: Earning Interest (20 minutes)
Activity
Students now explore the idea of repeated percent change in a banking or savings context. This may be a good time to more formally introduce the term compounding. They examine the effect of compounding 1% interest each month for a year. From the previous activity, students should recognize that the result will be more than 12% interest on the initial balance. This is because for each month after the first one, the amount used to calculate the interest includes previously earned interest, so that amount is higher than the initial balance. In future lessons, students will continue to investigate the effects of compounding interest in the long term.
To find the account balance at different times (the first question), students may choose to calculate the numerical values or to write expressions. Those who choose the latter will be in a better position to write a generalized expression for the account balance at any time. Select some students who chose different approaches to share their choice later.
Note that this activity simplifies what banks actually do to calculate interests. Financial institutions commonly calculate interest rates based on the number of days in the month or the year. The monthly interest rate for February, for instance, will be lower than that for March.
Launch
Give students a brief overview of savings accounts. Explain that when we deposit money in a savings account, we are allowing the bank to hold on to the money (and potentially use it to generate more revenue for the bank). In exchange, the bank pays us interest, that is a certain percentage of the money at a regular interval. The more money we put in the account, the more interest we earn. The interest calculation here works the same way as that for loans and credit cards, except that, in this case, higher interest rates and more-frequent interest calculations work in our favor, instead of against us.
Arrange students in groups of 2.
Supports accessibility for: Visual-spatial processing; Conceptual processing
Student Facing
A bank account has a monthly interest rate of 1% and initial balance of $1,000. Any earned interest is added to the account and no other deposits or withdrawals are made.
- What is the account balance after 6 months, 1 year, 2 years, and 5 years? Show your reasoning.
- Write an equation expressing the account balance (\(a\)) in terms of the number of months (\(m\)). Assume that all interest earned continues to be added to the account and no other deposits or withdrawals are made.
- How much interest will the account earn in 1 year? What percentage of the initial balance is that? Show your reasoning.
- The term annual return refers to the percent of interest an account holder could expect to receive in one year. Discuss with your partner: If you were the bank, would you advertise the account as having a 12% annual return? Why or why not? Use your work so far to explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may miss that the interest is applied monthly rather than annually. Help them read the question carefully, note this difference, and adjust the units to months for the appropriate questions.
Activity Synthesis
Ask previously selected students to share their strategies for the first question (using numerical values or using expressions). Highlight that writing expressions enables us to generalize and find the account balance for any time frame.
Select students to share how they found the interest earned over one year and what percentage it was of the initial balance. Make sure students understand that twelve successive increases of 1% yield a balance that is more than a single 12% increase. Then, invite groups to share which annual interest rate they would advertise if they were the bank.
Conclude by explaining that banking institutions call the two different interest rates different names. The 12% is called the nominal rate and the 12.68% the effective rate. The latter reflects the actual interest amount earned over a year, taking into account the monthly interest payment. This process of generating new earnings from previous earnings is called compounding. (In the context of loans, compounding refers to the generation of new debt from previous debts.)
As in the previous activity, the difference between the one-year interest calculated using the nominal rate versus the actual rate is not large. The differences become more and more pronounced, however, as time goes on.
Design Principle(s): Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
In this lesson, we compared the results of applying a percent increase (\(p\)) two successive times versus applying twice the percent (\(2p\)) one time. Give students the following example:
Two years ago, a pound of snow crab was priced at \$25 at both Store A and Store B. Last year, Store A increased the price by 20%. This year, it increased the price by 20% again. Store B increased its price by 40% this year.
Discuss questions such as:
- “Are the current snow crab prices at the two stores equal? Why or why not?”
- “Write an expression to represent the current price at each store. Which parts of the expressions are the same? Which parts are different?”
- “In which of the two pricing situations do we see compounding? What does it mean?”
- “Which option would result in more interest earned on a balance in a bank account: 1% interest calculated monthly or 6% calculated every six months? (Assume no money is added or removed from the account and the balance is left in the account for 6 months.) Why?”
16.4: Cool-down - Two Months Later (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Suppose a runner runs 4 miles a day this month. She is increasing her daily running distance by 25% next month, and then by 25% of that the month after. Will she be running 50% more than her current daily distance two months from now?
It is tempting to think that two months from now she will be running 6 miles, since twice of 25% is 50%, and 50% more than her current daily distance is \(4 \boldcdot (1.5)\). But if we calculate the increase one month at a time, we can see that next month she will run \(4 \boldcdot (1.25)\) or 5 miles. The month after that she will run \(5 \boldcdot (1.25)\) or 6.25 miles.
So two months from now her daily distance will actually be: \(\displaystyle 4 \boldcdot (1.25)^2\). Two repeated 25% increases actually lead to an overall increase of 56.25% rather than of 50%, because \(1.25^2=1.5625\). Applying a percent increase on an amount that has had a prior percent increase is called compounding.
Compounding happens when we calculate interest on money in a bank account or on a loan. An account that earns 2% interest every month does not actually earn 24% a year. Let's say a savings account has \$300 and no other deposits or withdrawals are made. The account balances after some months are shown in this table.
| number of months | account balance in dollars |
|---|---|
| 1 | \(300 \boldcdot (1.02)\) |
| 2 | \(300 \boldcdot (1.02)^2\) |
| 3 | \(300 \boldcdot (1.02)^3\) |
| 12 | \(300 \boldcdot (1.02)^{12}\) |
\((1.02)^{12} \approx 1.2682\), so the account will grow by about 26.82% in one year. This rate is called the effective interest rate. It reflects how the account balance actually changes after one year.
The 24% is called the nominal interest rate. It is the stated or published rate and is usually used to determine the monthly, weekly, or daily rates (if interest were to be calculated at those intervals).