Lesson 8
Spreadsheet Shortcuts
8.1: Tables of Equivalent Ratios (10 minutes)
Warm-up
The purpose of this activity is to prepare students to work with a table of equivalent ratios that appears in a later activity in this lesson.
Launch
Give students a few minutes to complete the table. Ensure that they found the correct values before they work on the second question.
Student Facing
Here is a table of equivalent ratios:
| \(a\) | \(b\) |
|---|---|
| 3 | 15 |
| 10 | 50 |
| 6 | 30 |
| 1 | |
| 80 |
- Complete the table with the missing values.
- Explain what it means to say that the pairs of numbers are equivalent ratios.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite students to share how they reasoned about the values needed to complete the table. Keep asking, "Did anyone think about it a different way?" until a few ways of reasoning come to light. Some methods might include
- multiplying any number in the first column by 5 to find the number in the second column
- dividing any number in the second column by 5 (or multiplying by \(\frac15\) to find the number in the first column)
- using a scale factor to move from row to row, for example, starting with 6 and 30, you can multiply each value by \(\frac16\) to find 1 and 5 in the next row.
8.2: The Birthday Trick (15 minutes)
Optional activity
The purpose of this activity is to learn that you can click on a cell to use its contents in a new expression rather than typing the address of the cell.
Launch
Ask students to write down the day and month of their birthday. Then, give them this sequence of instructions. Allow them to use a calculator if they wish. (Alternatively, you could have one student demonstrate the procedure on their birthday for the group, and then re-run the computations with each student using her own birthday.)
- Multiply the month by 5.
- Add 6.
- Multiply by 4.
- Add 9.
- Multiply by 5.
- Add the day.
- Subtract 165.
Tell students that they’ll program a spreadsheet to perform this trick, and learn a few shortcuts for using spreadsheets along the way.
Supports accessibility for: Language; Organization
Student Facing
Use the applet to answer the questions.
- In cell B4, we want to enter = B1 * 5 to multiply the month by 5. Enter this, but when you are about to type B1, instead, click on cell B1. This shortcut can be used any time: click on a cell instead of typing its address.
- Practice this technique as you program each cell in B5 through B10 to perform the right computation.
- When you are finished, does cell B10 show a number that contains the month and day of your birthday? If not, troubleshoot your computations.
- Try changing the month and day in cells B1 and B2. The rest of the computations should automatically update. If not, troubleshoot your computations.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Why does this trick work? Try using \(m\) for the month and \(d\) for the day, and writing the entire computation as an algebraic expression. Can you see why the resulting number contains the month and day?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Ask students to write down the day and month of their birthday. Then, give them this sequence of instructions. Allow them to use a calculator if they wish. (Alternatively, you could have one student demonstrate the procedure on their birthday for the group, and then re-run the computations with each student using her own birthday.)
- Multiply the month by 5.
- Add 6.
- Multiply by 4.
- Add 9.
- Multiply by 5.
- Add the day.
- Subtract 165.
Distribute internet-enabled devices, and give students instructions to navigate to this lesson in the digital version of the materials.
Supports accessibility for: Language; Organization
Student Facing
Navigate to this activity in the digital version of the materials or to ggbm.at/djcz6fjf.
- In cell B4, we want to enter = B1 * 5 to multiply the month by 5. Enter this, but when you are about to type B1, instead, click on cell B1. This shortcut can be used any time: click on a cell instead of typing its address.
- Practice this technique as you program each cell in B5 through B10 to perform the right computation.
- When you are finished, does cell B10 show a number that contains the month and day of your birthday? If not, troubleshoot your computations.
- Try changing the month and day in cells B1 and B2. The rest of the computations should automatically update. If not, troubleshoot your computations.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Why does this trick work? Try using \(m\) for the month and \(d\) for the day, and writing the entire computation as an algebraic expression. Can you see why the resulting number contains the month and day?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may misunderstand the instructions and continue to refer each cell back to the number of their month. Each row after the first instruction is meant to refer back to the previous value.
Activity Synthesis
Ask students what new shortcut they learned in the spreadsheet. Namely, when students want to use the contents of the cell in a computation, they can click on a cell rather than type in its address. Ask students what other things they had to remember about using spreadsheets.
8.3: Using Spreadsheet Patterns (10 minutes)
Optional activity
The mathematical purpose of this activity is for students to become more efficient at entering values into a spreadsheet. In later units, students may wish to use the techniques in this activity to quickly compute the values of sequences by continuing the pattern.
Monitor for students who use a recursive formula, for example, typing = B2 + 2 in cell B3. Also look for students who use an explicit formula, like typing = A3 / 3 in cell B3. After students complete the first question, ask students to share their various spreadsheet formulas that work. Assure them that either is okay.
Launch
Supports accessibility for: Visual-spatial processing
Student Facing
The spreadsheet applet contains a table of equivalent ratios.
- Use spreadsheet calculations to continue the patterns in columns A and B, down to row 5. Pause for discussion.
- Click on cell A5. See the tiny blue square in the bottom right corner of the cell? Click it and drag it down for several cells and let go.
- Repeat this, starting with cell B5.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Supports accessibility for: Visual-spatial processing
Student Facing
Navigate to this activity in the digital version of the materials or to the URL, ggbm.at/wu9t7kkd.
The spreadsheet contains a table of equivalent ratios.
- Use spreadsheet calculations to continue the pattern in columns A and B, down to row 5. Pause for discussion.
- Click on cell A5. See the tiny blue square in the bottom right corner of the cell? Click it and drag it down for several cells and let go.
- Repeat this, starting with cell B5.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Tell students that the technique used in this activity extends a set of operations to additional cells in the spreadsheet. Invite students to experiment with extending some other patterns in the spreadsheet.
8.4: Cool-down - Doubling in a Spreadsheet (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Sometimes you want to create a list of numbers based on a rule. For example, let's say that the cost of a gym membership is a \$25 sign-up fee followed by monthly dues of \$35. We may want to know how much the membership will cost over the course of 6 months. We could use a spreadsheet and set it up this way:
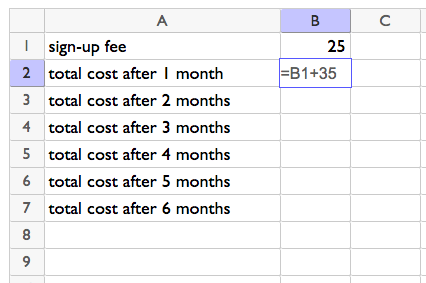
Which results in:
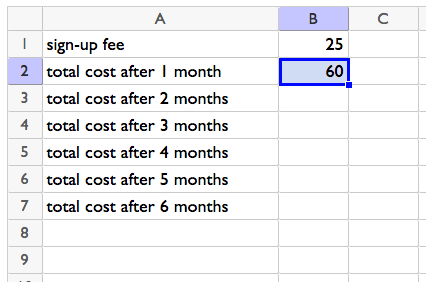
See the little square on the lower-right corner of cell B2? If we click and drag that down, it will keep adding 35 to the value above to find the value in the next row. Drag it down far enough, and we can see the total cost after 6 months.
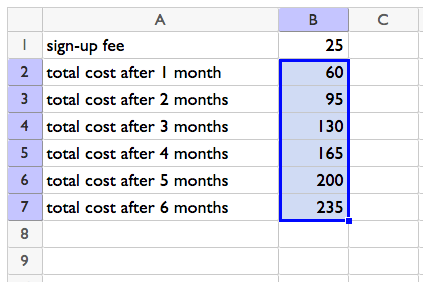
Any time you need to repeat a mathematical operation several times, continuing a pattern by dragging in a spreadsheet might be a good choice.