Lesson 5
Calculating Measures of Center and Variability
5.1: Calculating Centers (5 minutes)
Warm-up
The purpose of this warm-up is to encourage students to review how to calculate mean and median.
Launch
Display one problem at a time. Give students 1 minute of quiet think time followed by a whole-class discussion.
Student Facing
Decide if each situation is true or false. Explain your reasoning.
- The mean can be found by adding all the numbers in a data set and dividing by the number of numbers in the data set.
- The mean of the data in the dot plot is 4.
- The median of the data set is 9 for the data: 4, 5, 9, 1, 10.
- The median of the data in the dot plot is 3.5.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may forget to sort the data when finding the median. Ask them, “What is a median? What does it tell you about the data?” Some students may not remember how to find the median when there is an even number of data values. Ask them, “What does the median tell you about the data? How could we find a middle number between these two values?”
Activity Synthesis
The goal of this activity is to review how to calculate mean and median and to identify common mistakes in the calculation of mean and median. In the discussion, ask students to recall what information the mean and median reveal about the data.
- “What does the mean tell you about the data?” (On average, where the center of the data is.)
- “What does the median tell you about the data?” (Half of the numbers are greater than or equal to the median and half are less than or equal to the median.)
Some common mistakes to avoid:
- Not putting the numbers in order when finding the median.
- If two numbers are in the middle, not adding them and dividing by two to find the median.
- Finding the middle number on the horizontal axis rather than in the data.
- Rounding the mean to the nearest whole number.
5.2: Heartbeats: Part 1 (10 minutes)
Optional activity
The purpose of this activity is to get students to calculate the median and IQR, and to investigate how those values are impacted by outliers.
The data sets in this lesson are small enough that finding summary statistics like measures of center or measures of variability are not necessary. The entire data set could be assessed fairly easily and does not need further analysis. The sets are small here for the purposes of practicing calculating and understanding the statistics. In reality, finding such statistics are much more useful when the data set is much larger. For example, some devices will find heart rate every 10 minutes, giving more than 1,000 values for a week that might be analyzed to determine health information about a person. It would be difficult to understand all of the data by looking at a table or even a data display. Having some summary statistics such as mean or median would be useful to understand a person’s heart rate for the week.
In this activity, an optional graphic organizer is provided in the blackline master to help students compute the interquartile range. The boxes that are shaded are not to be used and the position of the open boxes are meant to highlight the useful data for calculating the value for the row. For example, to compute the first quartiles, students use the average of the second and third values, so those boxes are left open to indicate that this data is useful.
Launch
Give students 3–5 minutes of quiet time to work the first question and then pause for a brief whole-class discussion about how to calculate the median, quartiles, and IQR.
Supports accessibility for: Language; Organization
Student Facing
The heart rates of eight high school students are listed in beats per minute:
- 72
- 75
- 81
- 76
- 76
- 77
- 79
- 78
- What is the interquartile range?
- How many values in the data set are:
- less than Q1?
- between Q1 and the median?
- between the median and Q3?
- greater than Q3?
- A pod of dolphins contains 800 dolphins of various ages and lengths. The median length of dolphins in this pod is 5.8 feet. What information does this tell you about the length of dolphins in this pod?
- The same vocabulary test with 50 questions is given to 600 students from fifth to tenth grades and the number of correct responses is collected for each student in this group. The interquartile range is 40 correct responses. What information does this tell you about the number of correct responses for students taking this test?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may have difficulty calculating the median of a data set with an even number of data points. Ask them what the median represents for the data set and where that value might be. If they still struggle, remind them that the median is the average of the two middle numbers.
Activity Synthesis
The purpose of this discussion is to discuss the method of calculating median and IQR as well as the interpretation of each. Here are some questions for discussion.
- “What would a box plot look like for the results of the vocabulary test?” (It would depend on the high and the low score, but the box would likely start at 5 and go up to 45 or it could start at 10 and go up to 50.)
- “What does the IQR tell you about a data set?” (The IQR is a measure of variability which describes the range of the middle half of the data).
- “How do the median and quartiles divide the data?” (Into equal quarters so that the same number of values are in each quarter.)
- “How much of the data is between Q1 and Q3?” (The middle 50% of the data is between these values.)
5.3: Heartbeats: Part 2 (15 minutes)
Optional activity
The purpose of this activity is to get students to calculate and describe the mean absolute deviation. Students are given a data set and an organizer for calculating the MAD. Then, they consider questions that are intended to get them thinking about MAD more conceptually as a measure of variability.
Launch
Help students understand how to use the table by showing students the example table:
| data values | mean | deviation from mean (data value – mean) |
absolute deviation |deviation| |
|---|---|---|---|
| 1 | 5 | -4 | 4 |
| 2 | 5 | -3 | 3 |
| 3 | 5 | -2 | 2 |
| 4 | 5 | -1 | 1 |
| 5 | 5 | 0 | 0 |
| 6 | 5 | 1 | 1 |
| 7 | 5 | 2 | 2 |
| 12 | 5 | 7 | 7 |
This results in a MAD of 2.5 since \(\frac{4+3+2+1+0+1+2+7}{8} = 2.5\).
Student Facing
-
Calculate the MAD using the same data from the previous activity by finding the average distance from each data value to the mean. You may find it helpful to organize your work by completing the table provided.
data values mean deviation from mean
(data value - mean)absolute deviation |deviation| 72 75 81 76 76 77 79 78 MAD:
-
For another data set, all of the values are either 3 beats per minute above the mean or 3 beats per minute below the mean. Is that enough information to find the MAD for this data set? If so, find the MAD. If not, what other information is needed? Explain your reasoning.
-
Several pennies are placed along a meter stick and the position in centimeters of each penny is recorded. The mean position is the 50 centimeter mark and the MAD is 10 centimeters. What information does this tell you about the position of the pennies along the meter stick?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Suppose there are 6 pennies on a meter stick so that the mean position is the 50 centimeter mark and the MAD is 10 centimeters.
-
Find possible locations for the 6 pennies.
-
Find a different set of possible locations for the 6 pennies.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Monitor for students who have trouble finding the mean or who are using negative values for the distance from the mean. Remind them that the \(|x|\) symbol represents absolute value. If necessary, ask them to look at a number line and describe the distance between two values to remind them that distances should always be described as positive values.
Activity Synthesis
Put pennies on a meter stick so that the centers of the pennies are at {20, 40, 40, 45, 45, 45, 45, 55, 55, 55, 55, 55, 55, 90}. Show how the stick balances when you put your finger at the 50 centimeter mark and how some are farther and some are closer than 10 centimeters away from the mean, but they’re spread out so that, on average, they’re 10 cm away.
Create a display that incorporates the measures of center (mean and median) and variability (interquartile range and mean absolute deviation) discussed so far. Later, standard deviation will be added to the variability section. This display should be posted in the classroom for the remaining lessons within this unit. It should look something like:
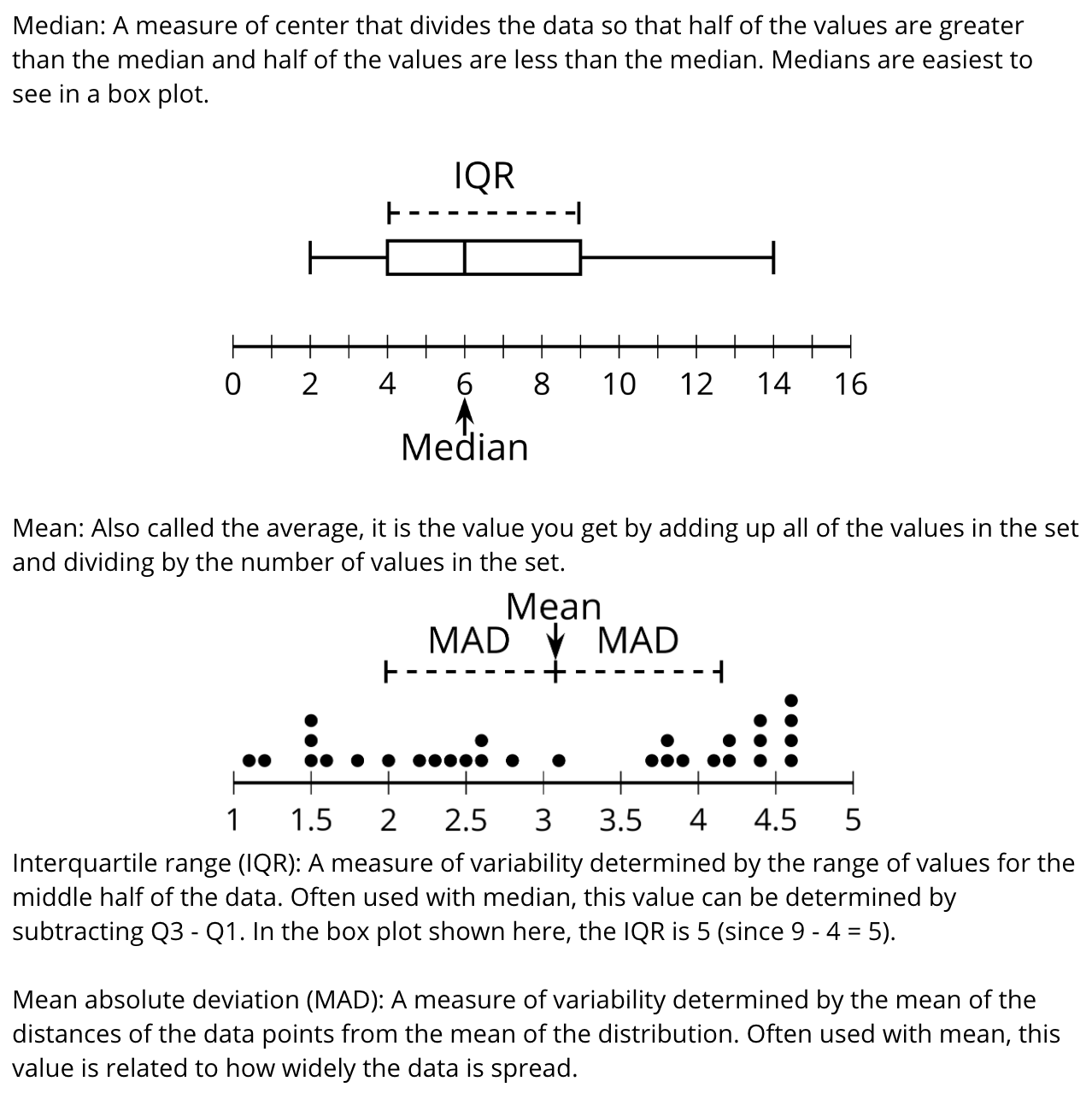
Here are some questions for discussion.
- “If you put pennies at 45, 35, and 70, where do you need to put a penny for the meter stick to balance at 50 cm? What is the MAD?” (50 cm, 10 cm)
- “If you put two pennies at 60, where do you need to put a penny to make the meter stick balance at 50 cm? What is the MAD?” (30 cm, \(\frac{40}{3}\) cm)
Supports accessibility for: Conceptual processing; Visual-spatial processing
Lesson Synthesis
Lesson Synthesis
The goal is to make sure students know how to calculate MAD and IQR and that they are measures of variability.
- “How do you calculate the IQR?” (Find the difference between the value of the third and first quartiles.)
- “How do you calculate the MAD?” (Find the distance of each value from the mean. Then take the mean of those values.)
- “One data set has a greater IQR than another. What does this mean about the data in the first data set?” (It has greater variability. This means that the middle half of the data is more spread out from the center than the middle half of the data from the second data set.)
5.4: Cool-down - Calculating MAD and IQR (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The mean absolute deviation, or MAD, and the interquartile range, or IQR, are measures of variability. Measures of variability tell you how much the values in a data set tend to differ from one another. A greater measure of variability means that the data is more spread out while a smaller measure of variability means that the data is more consistent and close to the measure of center.
To calculate the MAD of a data set:
- Find the mean of the values in the data set.
- Find the distance between each data value and the mean on the number line:
|data value – mean|
- Find the mean of the distances. This value is the MAD.
To calculate the IQR, subtract the value of the first quartile from the value of the third quartile. Recall that the first and third quartile are included in the five number summary.

