Lesson 12
Standard Deviation
12.1: Notice and Wonder: Measuring Variability (5 minutes)
Warm-up
The purpose of this warm-up is to elicit the idea that calculating the standard deviation is very similar to calculating the MAD, which will be useful when students explore standard deviation in a later activity. While students may notice and wonder many things about these dot plots, the similarities and differences between standard deviation and the MAD as measures of variability are the important discussion points.
Launch
Display the dot plots and statistics for all to see. Ask students to think of at least one thing they notice and at least one thing they wonder. Give students 1 minute of quiet think time, and then 1 minute to discuss the things they notice with their partner, followed by a whole-class discussion.
Student Facing
What do you notice? What do you wonder?
mean: 10, MAD: 1.56, standard deviation: 2

mean: 10, MAD: 2.22, standard deviation: 2.58

mean: 10, MAD: 2.68, standard deviation: 2.92

mean: 10, MAD: 1.12, standard deviation: 1.61

mean: 10, MAD: 2.06, standard deviation: 2.34

mean: 10, MAD: 0, standard deviation: 0

Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share the things they noticed and wondered. Record and display their responses for all to see. If possible, record the relevant reasoning on or near the images. After all responses have been recorded without commentary or editing, ask students, “Is there anything on this list that you are wondering about now?” Encourage students to respectfully disagree, ask for clarification, or point out contradicting information. If the concept of variability does not come up during the conversation, ask students to discuss this idea.
12.2: Investigating Standard Deviation (20 minutes)
Activity
The purpose of this activity is to let students investigate what happens to the standard deviation using different data sets. The goal is for students to make conjectures about what standard deviation measures and how relative size of the standard deviation can be estimated from the shape of the distribution. In particular, students should recognize that adding or subtracting the same value from each value in the data set will change the mean by the same amount, but the standard deviation remains unchanged. Multiplying or dividing each value in the data set by the same value scales both the mean and standard deviation by the same value.
Monitor for students who
- Check values without much thought until the mean or standard deviation is correct.
- Use a starting set of values, then modify a few of them up or down to match the statistics given.
- Use symmetry to get the mean correct.
- Adjust the data by multiplying all of the values by a number to change the spread of the distribution to get close to the standard deviation.
Identify students who create data sets with different types of distributions for “10 different numbers that have a mean of 1” and “10 different numbers with a standard deviation as close to 2.5 as you can get in one minute.”
Launch
Demonstrate how to find standard deviation and mean using the technology available. In Algebra 1, students are dealing with the entire population, not sampling, so the population standard deviation is used.
Open the Spreadsheet & Statistics tool from Math Tools, or navigate to https://www.geogebra.org/classic/spreadsheet. Enter the values in column A. Select all of column A, and then choose the button that looks like a histogram and “One Variable Analysis.” Click the button that says \(\Sigma x\). The population standard deviation is labeled \(\sigma\). Additionally, the spreadsheet command =SD(A1:A10) will compute the population standard deviation for data in cells A1 through A10.
Arrange students in groups of 2. Give students time to work through the first two questions, followed by a whole-class discussion.
Student Facing
Use technology to find the mean and the standard deviation for the data in the dot plots.
- What do you notice about the mean and standard deviation you and your partner found for the three dot plots?
- Invent some data that fits the conditions. Be prepared to share your data set and reasoning for choice of values.
Partner 1
Partner 2
Dot plots:



Dot plots:



Conditions:
- 10 numbers with a standard deviation equal to the standard deviation of your first dot plot with a mean of 6.
- 10 numbers with a standard deviation three times greater than the data in the first row.
- 10 different numbers with a standard deviation as close to 2 as you can get in 1 minute.
Conditions:
- 10 numbers with a standard deviation equal to the standard deviation of your first dot plot with a mean of 12.
- 10 numbers with a standard deviation four times greater than the data in the first row.
- 10 different numbers with a standard deviation as close to 2 as you can get in 1 minute.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of this discussion is to understand that the standard deviation is a measure of variability related to the mean of the data set. The discussion also provides an opportunity for students to discuss what they notice and wonder about the mean and standard deviation.
Select previously identified students in the order listed in the narrative to share their distributions and methods for finding values that worked.
For at least one student’s data set that had a standard deviation close to 2.5, ask them how they might adapt the data so that it has a mean of 1. (Shift the data up or down so that it has a mean of 1.)
Here are some questions for discussion.
- “What do you think that standard deviation measures? Why do you think that?” (I think that it measures variability because it behaved like MAD. When all the values were the same it was zero.)
- “Why is the standard deviation the same for {1,2,3,4,5} and {-2,-1,0,1,2}?” (For each data set: 1) the values to the left of the mean are a distance of 2 and 1 from the mean and the values to the right of the mean are a distance 2 and 1 from the mean, and 2) the middle value is 0 away from the mean. This results in the standard deviation being the same.)
- “Why is the standard deviation different for {-4, -2, 0, 2, 4} and {-4, -3, -2, -1, 0}?” (The values for the first data set are twice the distance from the mean as the values in the second data set. That makes the standard deviation for the first set greater than the standard deviation of the second data set.)
- “When is the standard deviation equal to zero?” (It is zero when all the values are the same as each other or when there is no variability.)
- “Was your mean the same as your partner’s mean in the fifth match?” (Answers vary. Sample response: My mean was much different from my partners. Mine was 5 and theirs was 10.)
- “How did using technology help or hinder your mathematical thinking about standard deviation and mean?” (It really helped me because I did not get bogged down with the calculations and I could look for patterns in the data, the data displays, and the statistics. In particular, having to come up with my own data and then see what happened to the statistics was really helpful.)
Supports accessibility for: Language; Organization
12.3: Investigating Variability (10 minutes)
Activity
The purpose of this mathematical activity is to let students investigate how the standard deviation and other measures of variability change when you add, change, or remove values in a data set. Monitor for students mentioning the concepts of shape, variability, and center. This activity works best when each student has access to statistical technology because it would take too long to do otherwise. If students don't have individual access, projecting the statistical technology would be helpful during the launch.
Launch
Open the Spreadsheet & Statistics tool from Math Tools, or navigate to https://www.geogebra.org/classic/spreadsheet. Demonstrate how to add, change, and remove data points from a data set using technology. Provide access to statistical technology. Give students time to work through the questions then pause for a brief whole-class discussion.
Supports accessibility for: Language; Organization
Student Facing
Begin with the data:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
- Use technology to find the mean, standard deviation, median, and interquartile range.
- How do the standard deviation and mean change when you remove the greatest value from the data set? How do they change if you add a value to the data set that is twice the greatest value?
- What do you predict will happen to the standard deviation and mean when you remove the least value from the data set? Check to see if your prediction was correct.
- What happens to the standard deviation and mean when you add a value to the data set equal to the mean? Add a second value equal to the mean. What happens?
- Add, change, and remove values from the data set to answer the question: What appears to change more easily, the standard deviation or the interquartile range? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
How is the standard deviation calculated? We have seen that the standard deviation behaves a lot like the mean absolute deviation and that is because the key idea behind both is the same.
-
Using the original data set, calculate the deviation of each point from the mean by subtracting the mean from each data point.
-
If we just tried to take a mean of those deviations what would we get?
-
There are two common ways to turn negative values into more useful positive values: take the absolute value or square the value. To find the MAD we find the absolute value of each deviation, then find the mean of those numbers. To find the standard deviation we square each of the deviations, then find the mean of those numbers. Then finally take the square root of that mean. Compute the MAD and the standard deviation of the original data set.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students who compute a different standard deviation may be using the sample standard deviation statistic. Tell these students to use the value for \(\sigma\) rather than \(s\) for computations in this unit.
Activity Synthesis
The purpose of this discussion is to talk about standard deviation as a measure of variability. The goal of this discussion is to make sure that students understand that the standard deviation behaves similarly to the MAD and that it is a measure of variability that uses the mean as a measure of center. Discuss how the standard deviation is impacted by the addition and removal of outliers in the data set. The standard deviation decreases when outliers are removed because the data in the distribution display less variability and the standard deviation increases when outliers are added because the data in the distribution display more variability.
Add standard deviation to the display of measures of center and measures of variability created in an earlier lesson.
- Standard deviation: A measure of variability often used with mean that describes the spread of the data. It is a more mathematically useful measure of variability than MAD.
- The MAD already included in the example display is approximately 1.09 and the standard deviation is 1.194.
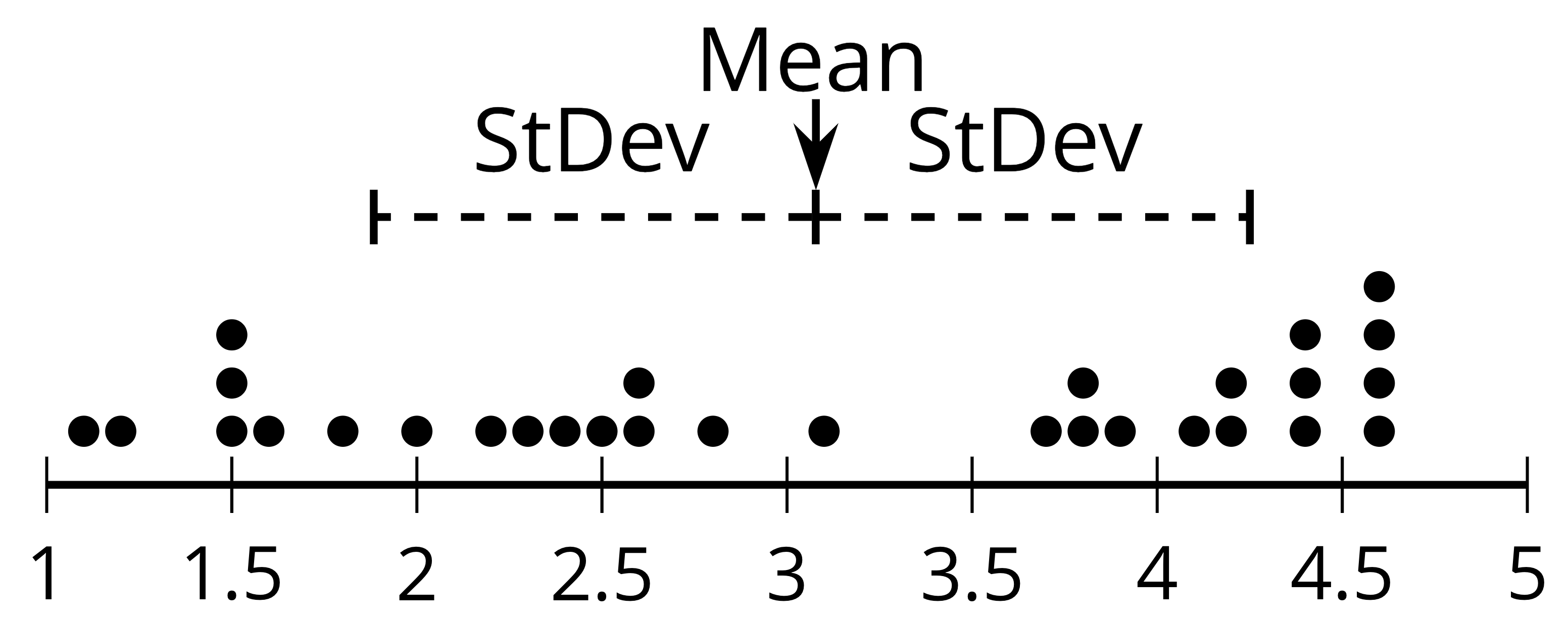
Here are some discussion questions.
- “What does the standard deviation measure? How do you know?” (It measures variability. Like the MAD, the standard deviation increases when outliers are included in the data set.)
- “The standard deviation is calculated using the mean, do you think it is more appropriate to use with symmetric or skewed data sets?” (Symmetric, because it is calculated using the mean.)
Lesson Synthesis
Lesson Synthesis
Here are some questions for discussion.
- “How does standard deviation compare and contrast with MAD and IQR?” (Like the MAD and IQR, the standard deviation is a measure of variability. Unlike the IQR, standard deviation is based on the mean not the median. It is very similar to the MAD because it involves finding the difference of each value and the mean, but then you perform different operations with those differences.)
- “One data set has a standard deviation of 5 and another data set has a standard deviation of 10. What does this tell you about the distribution of each data set?” (Standard deviation is a measure of variability so it tells you how spread apart the data are. The second data set shows greater variability than the first data set.)
12.4: Cool-down - True or False: Reasoning with Standard Deviation (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
We can describe the variability of a distribution using the standard deviation. The standard deviation is a measure of variability that is calculated using a method that is similar to the one used to calculate the MAD, or mean absolute deviation.
A deeper understanding of the importance of standard deviation as a measure of variability will come with a deeper study of statistics. For now, know that standard deviation is mathematically important and will be used as the appropriate measure of variability when mean is an appropriate measure of center.
Like the MAD, the standard deviation is large when the data set is more spread out, and the standard deviation is small when the variability is small. The intuition you gained about MAD will also work for the standard deviation.