Lesson 3
Metric Conversion and Multiplication by Powers of Ten
Warm-up: Number Talk (10 minutes)
Narrative
Launch
- Display one expression.
- “Give me a signal when you have an answer and can explain how you got it.”
- 1 minute: quiet think time
Activity
- Record answers and strategy.
- Keep expressions and work displayed.
- Repeat with each expression.
Student Facing
Find the value of each expression mentally.
- \(100 \times 1.5\)
- \(1,\!000 \times 1.5\)
- \(15 \div 10\)
- \(15 \div 100\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “What is the same about the values of the expressions?” (There is a 1 and a 5 in each value.)
- “What is different about the values of the expressions?”(Some of them are whole numbers and some are decimals.)
Activity 1: How Tall? How Long? How Far? (20 minutes)
Narrative
- When students convert from meters to centimeters or multiply by 100, the digits shift 2 places to the left.
- When students convert from kilometers to meters or multiply by 1,000, the digits shift 3 places to the left.
Supports accessibility for: Conceptual Processing, Memory
Required Materials
Materials to Gather
Launch
- Groups of 2
- Give students access to meter sticks.
- Display image from student workbook.
- “What do you notice? What do you wonder?”
- Display additional information about track and field events:
- The height of a hurdle is 1 meter.
- The approximate distance between hurdles in 110 meter races is 10 meters.
- The shortest race in many track competitions is 100 meters.
- “Work with you partner to complete the problems.”
Activity
- 1–2 minutes: quiet think time
- 8–10 minutes: partner work time
- Monitor for students who observe that:
- the digits shift 2 places to the left when converting from meters to centimeters or multiplying by 100
- the digits shift 3 places to the left when converting from kilometers to meters or multiplying by 1,000
Student Facing

- Complete the table.
meters centimeters millimeters 1 10 \(10^2\) - What patterns do you notice in the table?
- Three long-distance races are 10 kilometers, 100 kilometers, and 1,000 kilometers. How many meters are there in these races?
distance in kilometers distance in meters 1 1,000 10 100 \(10^3\) - What patterns do you notice in the table?
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
If students do not fill in the tables show them a meter stick and ask, “How can you use the meter stick to fill in the first row of the table?”
Activity Synthesis
- Display completed tables for all to see.
- Invite students to share patterns they observed in the tables.
- “How are the tables the same? How are they different?” (Some of the numbers in the tables are the same. Some of the relationships are the same. Going from meters to millimeters is the same as going from kilometers to meters because they are both 1,000 times greater. The second table only has two columns but has a bigger number, 1,000,000.)
- “What do you notice about the location of the 1 and the number of zeros after converting from kilometers to meters?” (Each number in the meters column has three more zeros than the number in the kilometers column. The one in each number in the meters column is three places to the left of the corresponding number in the kilometers column.)
Activity 2: Broad Jump (15 minutes)
Narrative
The purpose of this activity is for students to convert from meters to centimeters using the context of a standing broad jump, a common test for physical fitness. Students may multiply by 100 to convert from meters to centimeters or divide by 100 to convert from centimeters to meters. Students should be encouraged to use whatever strategy makes sense to them. Future lessons will focus specifically on conversion from centimeters to meters. Give students access to meter sticks.
Advances: Speaking
Required Materials
Materials to Gather
Launch
- Groups of 2
- Display the image from student workbook.
- Give students access to meter sticks.
- “What do you notice? What do you wonder?” (The girl is jumping. There are numbers on the mat. Did she start where the footprints are? How far did she jump?)
Activity
- 1–2 minutes: quiet think time
- 6–8 minutes: partner work time
- Monitor for students who:
- use their result for Tyler’s jump in centimeters to find his jump in millimeters
- use the result in meters to find how far Tyler jumped in millimeters
Student Facing

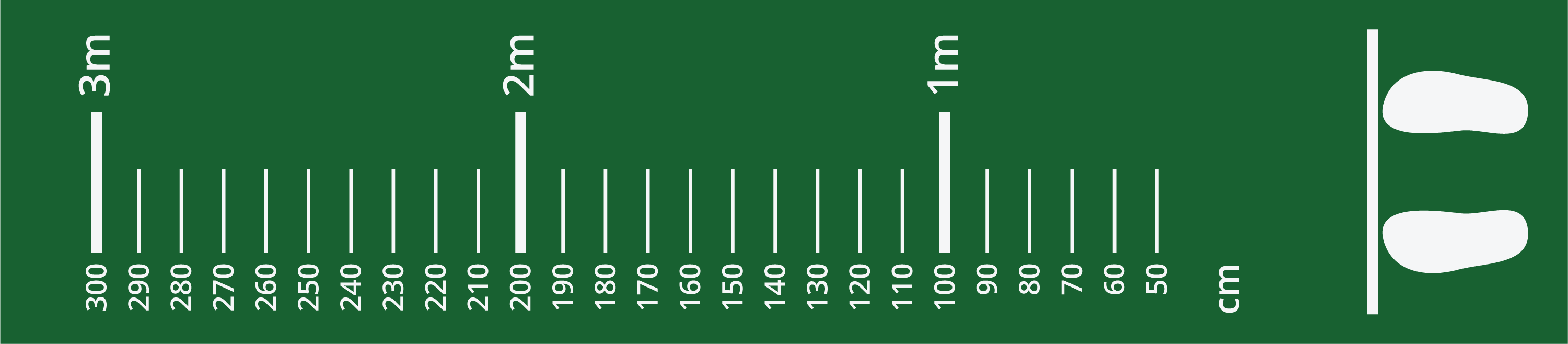
Here are the distances that each student jumped.
| student | distance |
|---|---|
| Mai | 1.61 meters |
| Tyler | 1.43 meters |
| Clare | 1.57 meters |
- The average standing broad jump distance for 5th graders is 148 centimeters. Are each of the students in the table below, at, or above the average? Explain or show your reasoning.
- The world record for the standing broad jump is 337 centimeters. Jada says that’s more than Mai and Clare jumped combined. Do you agree with Jada? Explain or show your reasoning.
- Tyler says his jump sounds more impressive if he reports it in millimeters.
- How far is Tyler’s jump in millimeters? What about Mai’s and Clare’s jumps?
- Which unit do you think is best for reporting the jumps? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
If students do not know the relationship between millimeters, centimeters, and meters, show them a meter stick and ask “How can you use the meter stick to figure out how many millimeters are in 1 meter?”
Activity Synthesis
- Display the expression: \(1.43 \times 100\).
- “How does this expression represent Tyler’s jump in centimeters?” (There are 100 centimeters in a meter.)
- Invite students to share how they found Tyler’s jump in millimeters.
- Display the expression: \((1.43 \times 100) \times 10\).
- “In what unit of measurement does this expression represent Tyler's jump? How do you know?” (It represents Tyler’s jump in millimeters. There are 10 millimeters in a centimeter and \(1.43\times100\) represents the centimeters, so if we multiply the number of centimeters by 10, we will get the number of millimeters.)
- Display the expression: \(1.43 \times 1,\!000\).
- “How does this expression represent Tyler’s jump in millimeters?” (There are 1,000 millimeters in a meter so I have to multiply by 1,000 to get millimeters from meters.)
- Display the equation: \(1.43 \times 1,\!000 = (1.43 \times 100) \times 10\).
- Invite students to share which unit they prefer to express the distances that the students jumped.
- “It’s important to choose a unit that makes sense to you.”
Lesson Synthesis
Lesson Synthesis
“Today we converted between metric units to express distances related to track events in different ways.”
Display a table that looks like this:
| kilometers | meters | centimeters | millimeters |
|---|---|---|---|
| 2.5 |
As students respond to the questions, record their responses in the table.
“Jada ran 2.5 kilometers. How many meters is that?” (2,500)
“How many centimeters is that?” (250,000)
“How many millimeters is that?” (2,500,000)
“Would you use kilometers, meters, centimeters, or millimeters to report how far Jada ran?” (Sample response: kilometers or meters because I can imagine how long those distances are and the numbers of centimeters and millimeters are too big to visualize.)
Cool-down: Kilometers (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.