Lesson 14
Representing Fractions on a Line Plot
Warm-up: Which One Doesn’t Belong: Line Plot (10 minutes)
Narrative
The purpose of this warm-up is for students to recall the line plots with fractional measurements which they have studied in prior courses. This prepares them to do more arithmetic with fractions using the data from line plots in the next two lessons.
Launch
- Groups of 2
- Display the image.
- “Pick one that doesn’t belong. Be ready to share why it doesn’t belong.”
- 1 minute: quiet think time
Activity
- “Discuss your thinking with your partner.”
- 2–3 minutes: partner discussion
- Share and record responses.
Student Facing
Which one doesn’t belong?




Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “Why doesn’t B belong?” (There are no fractions marked and there is no data with fractional values.)
- “Today we are going to work with line plots with fractional data and use what we have learned about fractions to solve problems.”
Activity 1: Sums of Fractions (15 minutes)
Narrative
The purpose of this activity is for students to make a line plot and answer questions about the data collected. The numbers that students plot come from spinning a spinner twice and adding the fractions on the spinner. The denominators are chosen so that 8 can be used as a common denominator. Students observe and think about patterns and then discuss them during the synthesis.
Supports accessibility for: Attention, Social-Emotional Functioning
Required Materials
Materials to Gather
Required Preparation
- Each group of 2 needs 1 paper clip and one pencil.
Launch
- Groups of 2
- Display the number line image from student workbook.
- “You are going to play a game with your partner. You will use a paper clip and a pencil to make a spinner out of the image in your workbook. Let’s practice.”
- Demonstrate how to use the pencil and paper clip as a spinner. Spin twice and record the fractions you landed on for all to see.
- “I need to find the value of the sum of these two fractions.”
- Demonstrate how to record the sum on the number line with an X.
- “Which number do you think will have the most Xs if you spin the spinner a lot of times? Why?”
- 1–2 minutes: partner discussion
Activity
- 1–2 minutes: quiet think time
- 6–8 minutes: partner work time
- Monitor for students who:
- partition the number line into eighths
- use common denominators to convert fractions with unlike denominators to fractions with like denominators
Student Facing
- Play Sums of Fractions with your partner.
- Take turns with your partner.
- Spin the spinner twice.
- Add the two fractions.
- Record the sum on the line plot.
- Play the game until you and your partner together have 12 data points.
- How did you know where to plot the sums of eighths?
- What is the difference between your highest and lowest number?
- What do you notice about the data you collected?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Ask previously identified students to share their thinking.
- “Did anyone record a one? What did you spin?” (I got \(\frac{1}{2}\) on both spins.)
- “Is there any other way to get 1 as a sum?” (No. I would need to add \(\frac{3}{4}\) to\(\frac{1}{4}\), \(\frac{7}{8}\) to \(\frac{1}{8}\), and \(\frac{3}{8}\) to \(\frac{5}{8}\) and none of those is possible.)
- “What is the largest number you recorded?” (Sample responses: \(1\frac{2}{8}\), \(1 \frac{1}{8}\))
- “Is it possible to get more than \(1\frac{2}{8}\)?” (No, the biggest number is \(\frac{5}{8}\) and two of those is \(1\frac{2}{8}\).)
- “Name a fraction that would have made the game more challenging if it were on the number mat. Why would this have made the game more challenging?” (\(\frac{2}{3}\), \(\frac{4}{5}\), or any other fraction with a denominator that is not a factor or multiple of 8. It would be more challenging because we could not use 8 as a common denominator to easily add the fractions.)
Activity 2: Lots of Eggs (20 minutes)
Narrative
The purpose of this activity is for students to use measurement data to make a line plot and then solve problems about the data presented in the line plot (MP2). The line plot is blank so students will choose which whole numbers to label and which fractions to label in between. They will use their understanding of equivalent fractions (halves, quarters, and eighths) to accurately make the line plot. Jada’s statement about the eggs that weigh \(1\frac{7}{8}\) ounces is interesting because it uses two fractions referring to different quantities: \(\frac{1}{4}\) is a fraction of the eggs and \(1\frac{7}{8}\) is their weight in ounces. The focus of the synthesis is on how students reason about Jada’s statement. As students reason through Jada’s statement, they critique the reasoning of others (MP3).
Advances: Reading, Representing
Launch
- Groups of 2
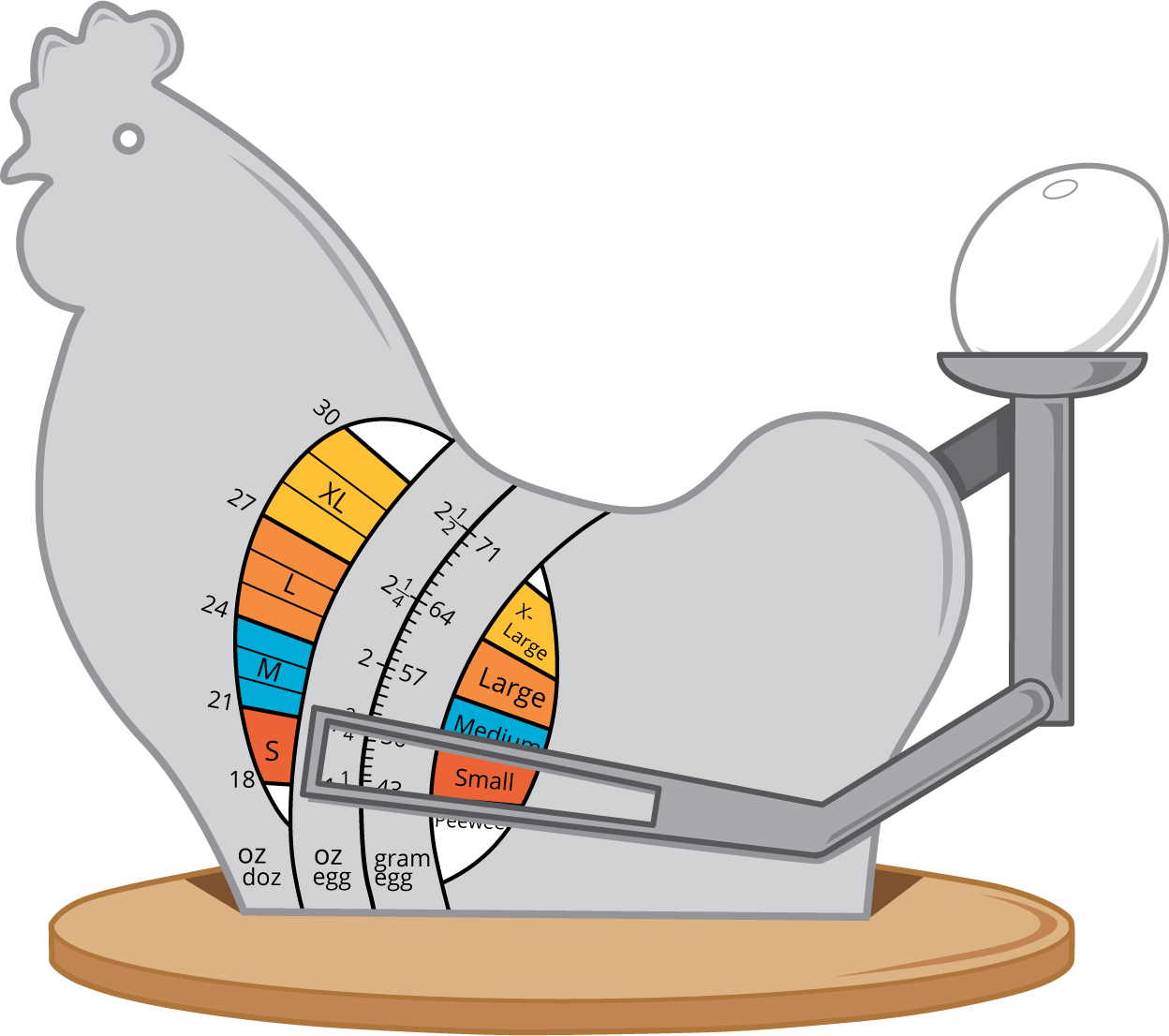
- Display the image.
- “What do you notice?” (It is a chicken. There is an egg. There are numbers and units.)
- “What do you wonder?” (What is it for? Is it a scale? Why does it say small, medium, large, X-Large?)
- “This is an egg scale. It is used to weigh eggs. What can you say about the egg on the scale?” (It's small. It weighs less than 2 ounces.)
- “Now you will make a line plot and answer questions about the egg weights.”
Activity
- 5 minutes: independent work time
- 5 minutes: partner work time
- Monitor for students who use either of these expressions to determine if Jada is correct:
- \(\frac{1}{4}\times12=3\)
- \(12\div4=3\)
Student Facing
-
Here are the weights of some eggs, in ounces. Use them to make a line plot.
\(1\frac{7}{8}\), \(2 \frac{1}{2}\), \(2\frac{3}{8}\), \(1 \frac{3}{4}\), \(2\frac{1}{4}\), \(2\frac{4}{8}\), \(2 \frac{1}{8}\), \(1\frac{7}{8}\), \(2\frac{1}{4}\), \(1\frac{6}{8}\), \(2\frac{1}{8}\), \(1\frac{7}{8}\)
- Jada said that \(\frac{1}{4}\) of the eggs weigh \(1\frac{7}{8}\) ounces. Do you agree? Explain or show your reasoning.
- How much heavier is the heaviest egg than the lightest egg? Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Ask previously selected students to share their response to Jada's statement.
- “How did you know how many eggs Jada weighed?” (I could count the measurements or count the marks on the graph.)
- “How did you decide if her statement was correct?” (I found \(\frac{1}{4}\) of 12 and then counted the number eggs that weighed \(1\frac{7}{8}\) ounces. They were both 3 so Jada is correct.)
- If students do not write an equation matching Jada’s response, consider displaying the equations \(\frac{1}{4} \times 12 = 3\) and \(12 \div 4 = 3\).
- “How do these equations represent Jada’s reasoning?” (They both say that \(\frac{1}{4}\) of the 12 egg measurements is 3 eggs. One uses multiplication and the other one uses division.)
Lesson Synthesis
Lesson Synthesis
“Today we made line plots and answered questions about the data in line plots.”
Display line plots from the student solutions for the 2 activities or use student-generated examples.
“How are the line plots the same?” (They both show data that is measured in fractions. The fractions are all eighths. There are 12 measurements in each line plot.)
“How are the line plots different?” (The numbers for the game are just numbers. The other ones are weights. The numbers for the game only go up to \(\frac{10}{8}\). There is more variation in the weights of the eggs.)
Cool-down: A Dozen Eggs (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.


