Lesson 1
Share Sandwiches
Warm-up: Which One Doesn't Belong: Sandwiches (10 minutes)
Narrative
This purpose of this warm-up is for students to compare four images. It introduces the context of sandwiches which will be used in the lesson to examine equal sharing situations, giving students a chance to engage with the context in an informal way before they interpret division situations about sharing sandwiches.
Launch
- Groups of 2
- Display the image.
- “Pick one that doesn’t belong. Be ready to share why it doesn’t belong.”
- 1 minute: quiet think time
Activity
- “Discuss your thinking with your partner.”
- 2–3 minutes: partner discussion
- Share and record responses
Student Facing
Which one doesn’t belong?



Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “What kind of sandwich do you like to eat? Are there special occasions when you eat sandwiches? Describe a time when you have shared food with your family or friends.”
Activity 1: Share Sandwiches (20 minutes)
Narrative
The purpose of this activity is for students to equally divide sandwiches in situations where the number of portions does not evenly divide the number of sandwiches. Students select the number of people sharing and the number of sandwiches from a small set of deliberately chosen numbers. Depending on their choice, each share may be less than a full sandwich or more than a full sandwich. This encourages students to make sense of the problem and persevere in solving it (MP1). The focus of the synthesis is on different ways students choose to make equal shares and how they know that the shares are equal. Many of the strategies for dividing the sandwiches equally are examined in detail in the next activity. In this activity, students explain how they know the shares are equal. Student representations may include coloring to show the equal shares. Monitor and select students who use the following strategies to share in the synthesis:
- choose numbers so each person gets one or two whole sandwiches and a fraction of a sandwich
- choose numbers so each person gets less than a full sandwich
Advances: Writing, Speaking, Listening
Launch
- Groups of 2
- Display the prompt without the questions.
__________ sandwiches are shared equally by __________ people. - “What do you notice? What do you wonder?” (There are no numbers. How many sandwiches are there? How many people are there? What kind of sandwiches are they?)
- “What are some numbers that would make sense? Why do those numbers make sense?” (One sandwich per person because that is a familiar serving size. Many people and many sandwiches because there is a party or event. More people than sandwiches because the people are sharing big sandwiches.)
Activity
- 2 minutes: independent think time
- 5–8 minutes: partner work time
- As students work, consider asking:
- “Where are the sandwiches in your drawing or diagram?”
- “How does your diagram or drawing show how much sandwich each person will get?”
Student Facing
__________ sandwiches are shared equally by __________ people.
- Choose numbers to fill in the blanks. You can only use each number once: 2, 3, 5.
- Represent the situation with a diagram or drawing.
- Explain or show how you know that each person will get the same amount of sandwich.
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
Students may recognize that the natural shape of their chosen sandwich impacts the size of certain pieces and, therefore, some people are getting a little bit more sandwich if they get a certain piece. When they recognize the constraints of the shape of a sandwich in real life, students are making sense of problems. Ask these students, “If you were going to share these sandwiches with your friends, which pieces would you want? Why would you want those pieces? Why do you think someone might choose the end pieces? Is it fair to say that each of you got about the same amount of sandwich?”
Activity Synthesis
- Ask the selected students to display their responses side by side for all to see.
- “Does each person get more than a full sandwich or less? How do you know?” (Less because there are more people than sandwiches or more because there are more sandwiches than people.)
- “This situation is about sharing. We can represent equal sharing situations with division expressions. What division expressions can we write to represent each of the situations we represented?” (Answers vary depending on number choices: \(2\div3\), \(3\div2\), \(2\div5\), \(5\div2\), \(3\div5\), \(5\div3\))
Activity 2: The Same Amount (15 minutes)
Narrative
In the previous activity students chose numbers to represent the sandwiches and the people sharing them and then represented those equal shares. The purpose of this activity is for students to explain how different representations can show equal shares when a division situation results in a quotient that is a fraction. Students have an opportunity to use their own language to describe equal shares in a division situation. Students may name the numerical amount of sandwich that each person gets, but that is not the focus of this activity. In future lessons, students will focus on numerical solutions for division situations that result in a quotient that is a fraction.
This activity uses MLR2 Collect and Display. Advances: Reading, Writing.
Supports accessibility for: Conceptual Processing, Memory
Launch
- Groups of 2
Activity
- 8–10 minutes: partner work
MLR2 Collect and Display
- Circulate, listen for, and collect the language students use to describe how they know each person gets the same amount.
- Listen for these words and phrases: divide, same, equal, fair, size of the piece, number of pieces, and one third of one half.
- Record students’ words, phrases, and expressions on a visual display and update it throughout the lesson.
Student Facing
- Han’s work shows how 3 people could equally share 2 sandwiches.
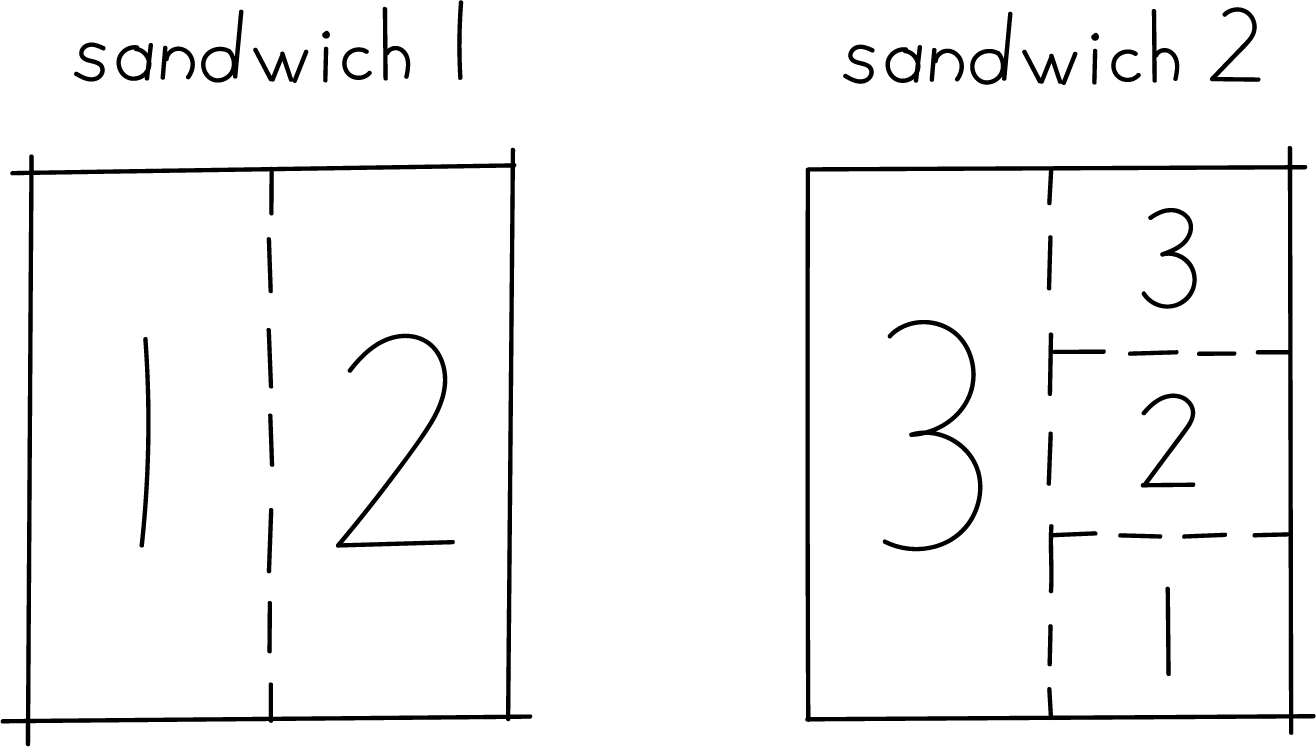
- Draw a diagram to show a different way that 3 people could share 2 sandwiches so each person got about the same amount of sandwich.
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
If students do not explain how they know that each person got the same amount of sandwich, consider asking: “How does the diagram represent the situation?”
Activity Synthesis
- Refer to the display.
- “These are the words, phrases, and expressions that you used when you were describing how you knew each person got the same amount of sandwich.”
- “Are there any other words or phrases that are important to include on our display?”
- As students share responses, update the display by adding (or replacing) language, diagrams, or annotations.
- Remind students to borrow language from the display as needed.
- Display: \(2 \div 3\)
- “How does this expression represent the situation that Han drew?” (There are 2 sandwiches being shared by 3 people.)
Lesson Synthesis
Lesson Synthesis
“Today, we represented division situations about people sharing sandwiches.”
Display the problems the students solved today.
Consider asking students to respond to these questions in their journal.
- “What was the same about all the problems we solved today?” (They were all about sandwiches. There was always a fraction of some sort. Both problems had the same numbers.)
- “What was different about the problems?” (The diagrams were different. Sometimes people got more than one whole sandwich and sometimes they got less than one whole sandwich. Sometimes the number represented sandwiches and sometimes it represented people.)
- “What is something you are still wondering about division?” (Can the answer be a fraction? What would happen if they were sharing a fraction of a sandwich?)
Cool-down: How Much? (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.