Lesson 5
Symmetry in Figures (Part 2)
Warm-up: Number Talk: Keeping Track (10 minutes)
Narrative
This Number Talk encourages students to think about place value and to rely on the structure of multi-digit numbers and properties of operations to mentally add multiple addends. The strategies elicited here help students develop fluency in adding multi-digit numbers. They will also be helpful when students reason about the perimeter and angles in line-symmetric figures.
Launch
- Display one expression.
- “Give me a signal when you have an answer and can explain how you got it.”
- 1 minute: quiet think time
Activity
- Record answers and strategy.
- Keep expressions and work displayed.
- Repeat with each expression.
Student Facing
Find the value of each expression mentally.
- \(43 + 57 + 50 + 7 + 3 + 40\)
- \(243 + 57 + 43 + 257\)
- \(1,\!043 + 257 + 57 + 200 + 43 + 1,\!000\)
- \(1,\!943 + 257 + 1 + 257 + 1,\!000 + 943\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “How did you use the first expression to help solve the expressions that follow?” (\(43 + 57 = 100\), so anywhere we see numbers with that combination being added, we can add 100 instead.)
- Consider asking:
- “Who can restate _____’s reasoning in a different way?”
- “Did anyone have the same strategy but would explain it differently?”
- “Did anyone approach the expression in a different way?”
- “Does anyone want to add on to _____’s strategy?”
Activity 1: Half-drawn Figures (15 minutes)
Narrative
In an earlier lesson, students observed that a line of symmetry decomposes a figure into two halves that match up exactly if the figure is folded along the line. This activity highlights that having two identical halves on each side of a line doesn’t necessarily make a figure symmetrical. It encourages students to use their understanding of symmetry and the line of symmetry to articulate why this is so as they critique supplied reasoning (MP3).
The given grid enables students to reason about the size and position of the attributes of each figure and provides structure for drawing the vertices and segments of each missing half.
Supports accessibility for: Visual Spatial Processing, Memory, Fine Motor Skills
Required Materials
Materials to Gather
Launch
- Groups of 2
- Give patty paper and a ruler or straightedge to each student.
Activity
- 2 minutes: quiet think time
- 3 minutes: partner discussion
- As students work, take note of students’ language when describing why Clare’s figures are incorrect.
- 3 minutes: independent work time
MLR 1 Stronger and Clearer
- “How do you know that your drawings have line symmetry?”
- “Share your explanation with 2–3 different partners. Revise your thinking, if needed, to make your explanation stronger each time.”
- 3–5 minutes: structured partner discussion
Student Facing
Each shaded triangle is half of a whole figure that has a line of symmetry shown by the dashed line.
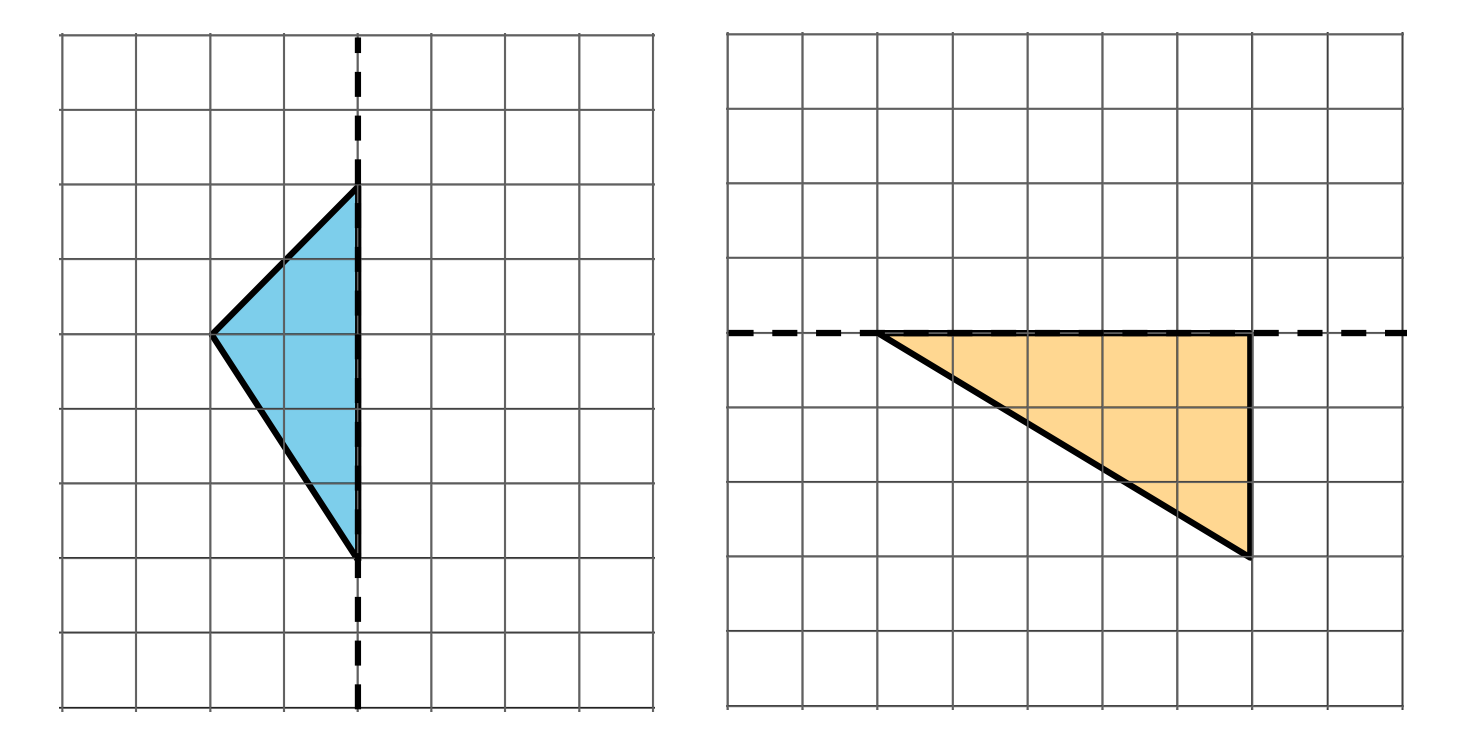
Clare drew in some segments to show the missing half of each figure.
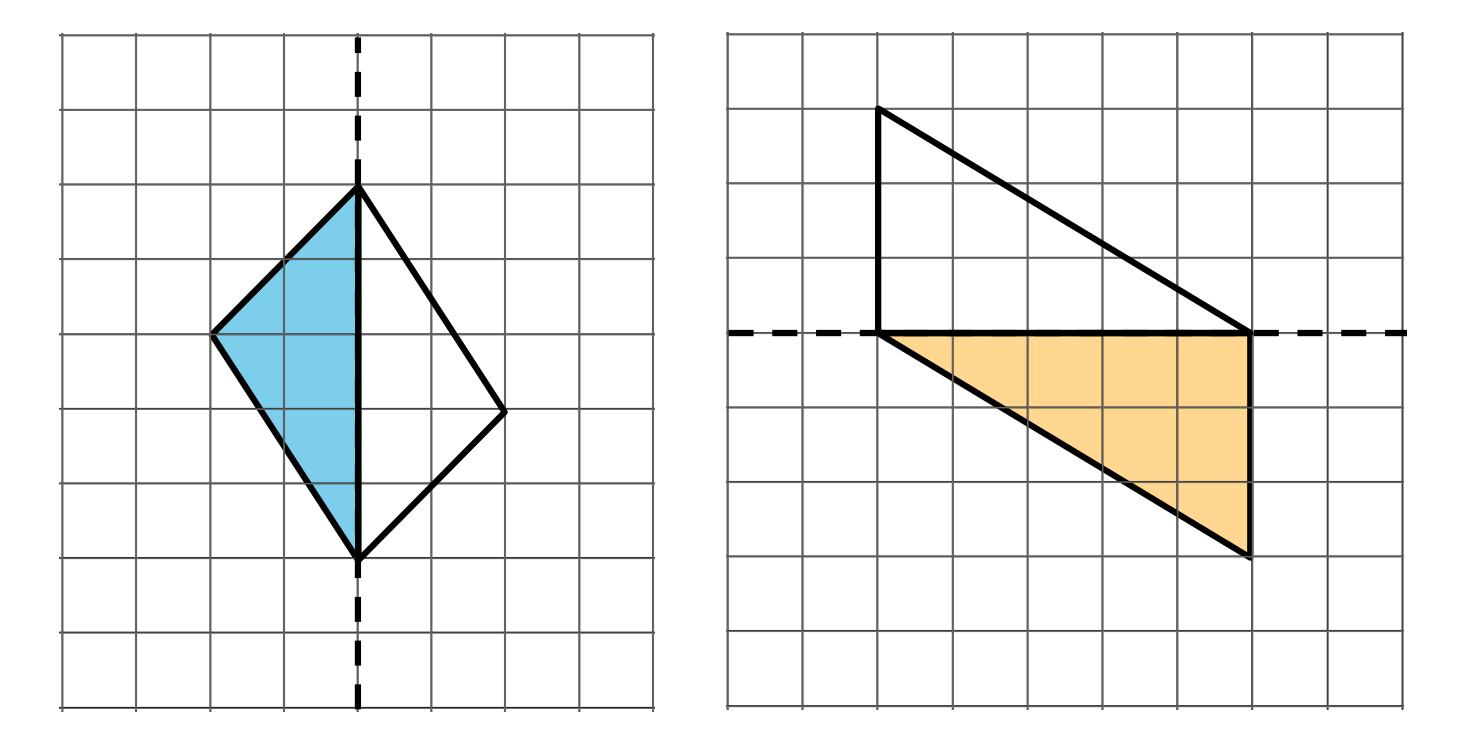
Do you agree that the dashed line is a line of symmetry for each figure Clare completed? Explain your reasoning. If you disagree with Clare's work, show a way to complete the drawing so the dashed line is a line of symmetry.
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
If students agree with Clare’s drawings or create another figure that has no line symmetry, consider asking:
- “How did you find lines of symmetry in yesterday’s lesson? How could you use that strategy to check if Clare’s figure has line symmetry?”
- “How could you use that strategy to create a figure with line symmetry?”
Activity Synthesis
- Invite 1–2 students to share their completed drawings. Compare and contrast them to Clare’s drawings.
- “What might be a possible reason for thinking that Clare’s drawings show the correct whole figures?” (The new halves are exactly the same figure and size as the given halves.)
- “How can we tell that Clare’s completed figures do not have line symmetry?” (The given half and the new half don’t match up when the figure is folded along the line.)
Activity 2: What’s the Whole Picture? (20 minutes)
Narrative
In this activity, students continue to reason about the missing half of a line-symmetric figure given half of the figure and a line of symmetry. A grid is given in some cases, but in others, students may choose an appropriate tool (MP5)—patty paper, paper cutouts, rulers, or protractors—to help them draw whole figures with some precision.
In the first problem, students use patty paper to help them draw line-symmetric figures. For some figures, students may rotate and slide—instead of reflect or flip—a traced figure to show the missing half. During the synthesis, highlight that sliding and rotating are not reliable for completing all line-symmetric figures. (For example, it is not possible to slide a copy of the half-star figure to show the full star.) Students learn that flipping the given half across the line of symmetry will consistently complete the symmetrical figure.
Advances: Listening, Representing
Required Materials
Materials to Gather
Launch
- Groups of 2
- Give a ruler or straightedge to each student.
- Provide access to patty paper, paper for cutting, protractors, and scissors.
Activity
- 6–8 minutes: independent work time
- Monitor for students who use tools to complete their drawings more precisely.
- 5–7 minutes: group discussion
Student Facing
- Here are three figures. Each figure is half of a whole figure. The dashed line is a line symmetry of that figure.
Use patty paper to help you draw the whole figure.
- Each figure on the grid is half of a whole figure that has a line of symmetry. The dashed line shows the line of symmetry. Use the grid to help you draw the whole figure. Be as precise as possible.
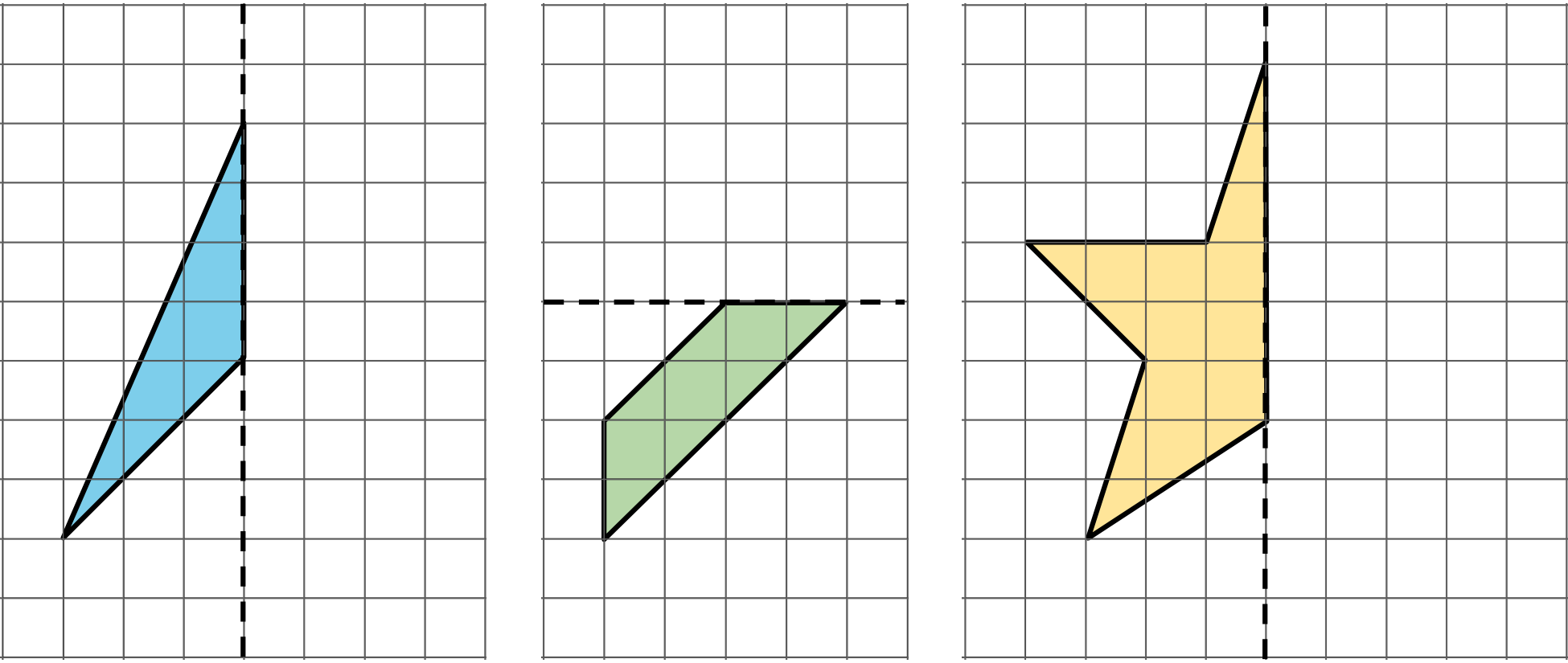
- Here is another figure that is half of a whole figure with a vertical line of symmetry. Draw the whole figure. Be as precise as possible.
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
If students draw freehand to complete the figures on the grid, consider asking:
- “How are you making sure the whole figure you create will have line symmetry?”
- “How can you use the grid to draw line segments so that your figure will have line symmetry?”
Activity Synthesis
- Invite previously identified students to share how they used the patty paper and other tools to complete the figures with the triangle, trapezoid, and rhombus halves.
- “How did the tools support you in drawing the whole figures?” (Sample responses:
- I traced or cut out one half of the figure and flipped it across the line of symmetry to make the whole figure.
- I measured the lengths and distances of different segments and copied the measurements to the other side to be sure the parts were equal.)
- “Did you use tools when drawing the whole figures that were on the grid? Why or why not?” (No, because the figures are on a grid. I could count the number of units to draw each missing half.)
Activity 3: What Could the Whole Figure Be? [OPTIONAL] (10 minutes)
Narrative
In the previous activities, students completed drawings of line-symmetric figures given half of each figure and a line of symmetry. In this optional activity, students do so again, but no lines of symmetry are given. Students are likely to find it intuitive to choose a side of the given shape—a triangle—and use it as a line of symmetry. The task prompts them to consider something less intuitive—that there may be multiple possible whole figures they could draw given half a figure.
A cutout of the triangle is given to encourage students to physically flip the shape along its different sides and trace the reflection, though students could also use other tools or methods to complete the task.
Required Materials
Materials to Gather
Materials to Copy
- Two Symmetrical Figures
Required Preparation
- Create a set of triangle cutouts from the blackline master for each group of 2.
Launch
- Groups of 2–4
- Give a set of triangle cutouts from the blackline master to each group.
- Give a ruler or straightedge to each student.
- Provide access to patty paper, rulers, protractors, and scissors, in case requested.
Activity
- 4 minutes: independent work time
- 2 minutes: group discussion
Student Facing
Trace a triangle cutout from your teacher.
If the triangle is half of a whole figure that has line symmetry, what could the whole figure look like? Can you show two possibilities? Three possibilities?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Invite students to share their completed drawings and their strategies.
- For each triangle, ask: “Are there other possible whole figures that are not yet shown?” Encourage students to identify any missing possibilities.
- “Did anyone use a strategy other than flipping the cutout along one side and tracing it? What was the strategy? How did it help you?”
- “Where is the line of symmetry in each completed drawing?” (It is the side used to reflect the given triangle, or the side shared by the two triangles.)
Lesson Synthesis
Lesson Synthesis
“Today we saw that, if given half of a figure and a line of symmetry, we can draw a full figure. If we wanted to, we can do that quite precisely.”
Display the last image from the second activity (What’s the Whole Picture?).

“Here’s half of a figure you saw earlier. What are some ways to find the other half so that the whole figure has line symmetry?” (Some ways:
- Trace the half-figure on patty paper and flip it over along the line of symmetry.
- Cut out the half-figure, flip it over along the line of symmetry, and trace the figure.
- Measure how far the points at each angle are from the line of symmetry and draw them on the other side of the line.
- Measure the lengths and angles in the half-figure and draw a mirror image with those lengths and angles.)
“How would you know if your drawing is correctly drawn?” (If we fold the drawing along the line of symmetry, the two halves would match up perfectly.)
Cool-down: Make Them Whole (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
