Lesson 9
Explain Equivalence
Warm-up: Number Talk: Familiar Numbers (10 minutes)
Narrative
This Number Talk encourages students to use the relationship between related numbers (5 and 10, and 6, 12, and 24) and properties of operations to find products. The strategies of doubling and halving elicited here will be helpful later in the lesson when students generate equivalent fractions. In describing strategies, students need to be precise in their word choice and use of language (MP6).
Launch
- Display one expression.
- “Give me a signal when you have an answer and can explain how you got it.”
- 1 minute: quiet think time
Activity
- Record answers and strategy.
- Keep expressions and work displayed.
- Repeat with each expression.
Student Facing
Find the value of each expression mentally.
- \(10\times6\)
- \(10\times12\)
- \(10\times24\)
- \(5\times24\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “How did the first three expressions help you find the value of the last one?”
Activity 1: Pointed Discussion (20 minutes)
Narrative
In this activity, students look closely at the relationships of fractions with denominator 5, 10, and 100. They use their observations and understanding to identify equivalent fractions and to explain why two fractions are or are not equivalent. When students analyze and criticize the reasoning presented in the activity statements and when the discuss their work with classmates, they are critiquing the reasoning of others and improving their arguments (MP3).
Supports accessibility for: Social-Emotional Functioning
Required Materials
Materials to Gather
Launch
- Groups of 2
- Give students access to rulers or straightedges.
- Ask students to keep their materials closed.
Activity
- “Take 5 quiet minutes to answer the problem. Afterwards, discuss your thinking with your partner.”
- 5 minutes: independent work time
- 5 minutes: partner discussion
Student Facing
Andre, Lin, and Clare are representing \(\frac{70}{100}\) on a number line.

- Andre said, “Oh, no! We’ll need to partition the line into 100 equal parts and count 70 parts just to mark one point!”
- Lin said, “What if we mark \(\frac{7}{10}\) instead? We could partition the line into just 10 parts and count 7 parts.”
- Clare said, “What if we partition the line into 5 parts and mark \(\frac{3}{5}\)?”
Do you agree with any of them? Explain or show your reasoning.



Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
MLR1 Stronger and Clearer Each Time
- “Share your reasoning and number lines with your partner. Take turns being the speaker and the listener. If you are the speaker, share your ideas and writing so far. If you are the listener, ask questions and give feedback to help your partner improve their work.”
- 3–5 minutes: structured partner discussion
- Repeat with 2–3 different partners.
- “Revise your initial draft based on the feedback you got from your partners.”
- 2–3 minutes: independent work time
Activity 2: How Do You Know? (15 minutes)
Narrative
This activity gives students opportunities to practice explaining or showing whether two fractions are equivalent. Students may do so using a visual representation, by reasoning about the number and size of the fractional parts in each fraction, or by thinking about multiplicative relationships between the numbers in the given fractions.
Students participate in a gallery walk in which they generate equivalent fractions for the numbers on the posters. Students visit at least two of six posters (or as many as time permits)—at least one poster with two fractions (posters A–C) and one poster with three fractions (posters D–F). Here are the sets shown on the blackline master:
A
\(\frac{2}{10}\), \(\frac{20}{100}\)
B
\(\frac{6}{4}\), \(\frac{18}{12}\)
C
\(\frac{3}{5}\), \(\frac{60}{100}\)
D
\(\frac{1}{4}\), \(\frac{3}{12}\), \(\frac{30}{100}\)
E
\(\frac{15}{6}\), \(\frac{7}{4}\), \(\frac{30}{12}\)
F
\(\frac{7}{3}\), \(\frac{21}{10}\), \(\frac{28}{12}\)
Because at the posters with two fractions (A–C) students would need to generate an equivalent fraction that hasn’t already been written by others, generating equivalent fractions becomes more difficult as the activity goes on. Consider using this to differentiate for students who may need an additional challenge: start them at the posters with three fractions (D–F).
Advances: Speaking, Conversing
Required Materials
Required Preparation
- Each group needs 4 sticky notes.
Launch
- Groups of 3–4
- Give each group 4 sticky notes
- Read the task statement as a class. Solicit clarifying questions from students.
- Invite a couple of students to recap the directions in their own words or to demonstrate the process, if helpful.
- Consider assigning each group a starting poster and giving directions for rotation.
Activity
- 10 minutes: gallery walk
- Tell students who are visiting posters A–C that they could leave feedback about the fraction on a sticky note if they disagree that it is equivalent to the fractions on the poster. They should include their name and be prepared to explain how they know.
Student Facing
Around the room you will find six posters, each showing either two or three fractions.
With your group, visit at least two posters: one with two fractions and one with three fractions.
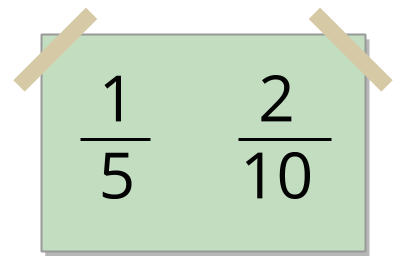
For the set of 2 fractions:
- Explain or show how you know the fractions are equivalent.
- Write a new equivalent fraction on a sticky note and add it to the poster. Think of a fraction that hasn’t already been written by someone else.
We visited poster __________, which shows __________ and __________.
New equivalent fraction: __________
For the set of 3 fractions:
-
Identify 2 fractions that are equivalent. Explain your reasoning.
We visited poster __________, which shows __________, __________, and __________.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- See lesson synthesis.
Lesson Synthesis
Lesson Synthesis
Select a group to share their response and reasoning for each poster.
Highlight visual diagrams or verbal explanations that clearly show how the number and size of the parts of two fractions can differ even though the fractions are the same size.
When students explain their work on posters D–F, ask about the non-equivalent fraction. For instance: “How did you know that \(\frac{1}{4}\) and \(\frac{3}{12}\) are equivalent but \(\frac{30}{100}\) is not equivalent to them?”
Cool-down: To Be or Not to Be (Equivalent) (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.