Lesson 2
How Did You Add?
Warm-up: Choral Count: Count Back From 70 (10 minutes)
Narrative
The purpose of this Choral Count is to invite students to practice counting backward by 1 and notice patterns in the count. When students describe repeated patterns they see using the language of place value, they look for and make use of the base-ten structure of numbers and connect it to the counting sequence (MP6, MP7, MP8).
Launch
- “Count backward by 1, starting at 70.”
- Record as students count.
- Stop counting and recording at 20.
Activity
- “What patterns do you see?”
- 1-2 minutes: quiet think time
- Record responses.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “Who can restate the pattern in different words?”
Activity 1: Find the Value (15 minutes)
Narrative
The purpose of this activity is for students to add 2 two-digit numbers within 100, without composing a ten, in a way that makes sense to them. Students may apply methods such as counting on or adding tens and tens and ones and ones. Monitor and select students with the following methods to share in the synthesis:
- counts on from 23 or 45 by tens and ones, (\(23 + 10 + 10 + 10 + 10 = 63\), \(63 + 1 + 1 + 1 + 1 +1 = 68\) or \(45 + 10 + 10 = 65\), \(65 + 1 + 1 + 1 = 68\))
- adds to 23 or 45 by adding all the tens and then all the ones (\(23 + 40 + 5\) or \(45 + 20 + 3\))
- combines tens and tens and ones and ones (\(20 + 40 = 60\), \(3 + 5 = 8\), \(60 + 8 = 68\) or \(3 + 5 = 8\), \(20 + 40 = 60\), \(60 + 8 = 68\))
During the synthesis, the teacher records each step of student thinking as equations as shown above. Students discuss connections between their classmates’ work.
Required Materials
Materials to Gather
Launch
- Groups of 2
- Give students access to connecting cubes in towers of 10 and singles.
Activity
- Read the task statement.
- 5 minutes: independent work time
- 2 minutes: partner discussion
- Monitor for students who use the methods described in the activity narrative.
Student Facing
Find the value of \(23 + 45\).
Show your thinking using drawings, numbers, or words.

Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
If students find a value other than 68, consider asking:
- “How did you find the value of 23 + 45?”
- “How could you use connecting cubes (or drawings) to find the value?”
- “How could you use labels or other drawings to keep track of how you counted?”
Activity Synthesis
- Invite previously identified student to share in the order presented above.
- As students explain their thinking, record drawings and equations.
- “Does anyone have a question about _____'s method?”
- “How are these methods and equations the same? How are they different?” (One person started with 23 and the other started with 45. They all worked with tens and ones. The first person counted on by ten and then by one. The next person added the tens and then the ones to the first number. The last person broke apart both numbers and added the tens together and the ones together.)
Activity 2: Elena and Andre Represent $63 + 25$ (10 minutes)
Narrative
The purpose of this activity is for students to analyze two different representations of addition methods and identify the equations that match each method. One of the representations shows adding tens and tens and ones and ones. The other representation shows counting on by tens and ones.
Advances: Listening, Speaking
Supports accessibility for: Visual-Spatial Processing, Conceptual Processing
Required Materials
Materials to Gather
Launch
- Groups of 2
- Give students access to connecting cubes in towers of 10 and singles.
- Display and read the first problem.
- “Look at each student’s work and see if you can figure out what they were each thinking.”
- 1 minute: quiet think time
- 1 minute: partner discussion
- Share student responses.
Activity
- Display and read the second problem.
- “Which equations go with each drawing? Be ready to explain how you know so that others will understand.”
- 3 minutes: partner discussion
Student Facing
-
Here are 2 drawings students made for \(63 + 25\).
Elena's work
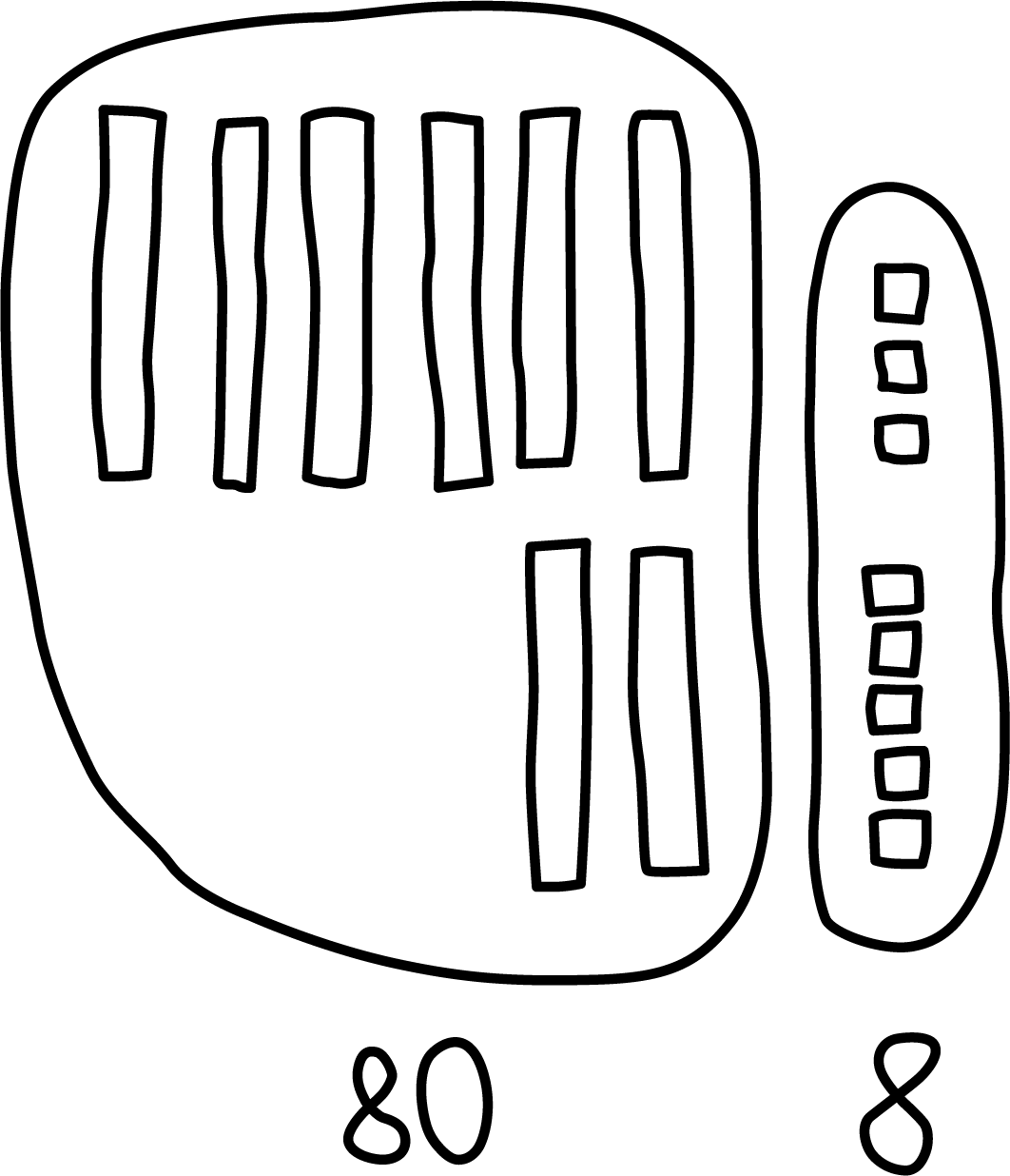
Andre's work
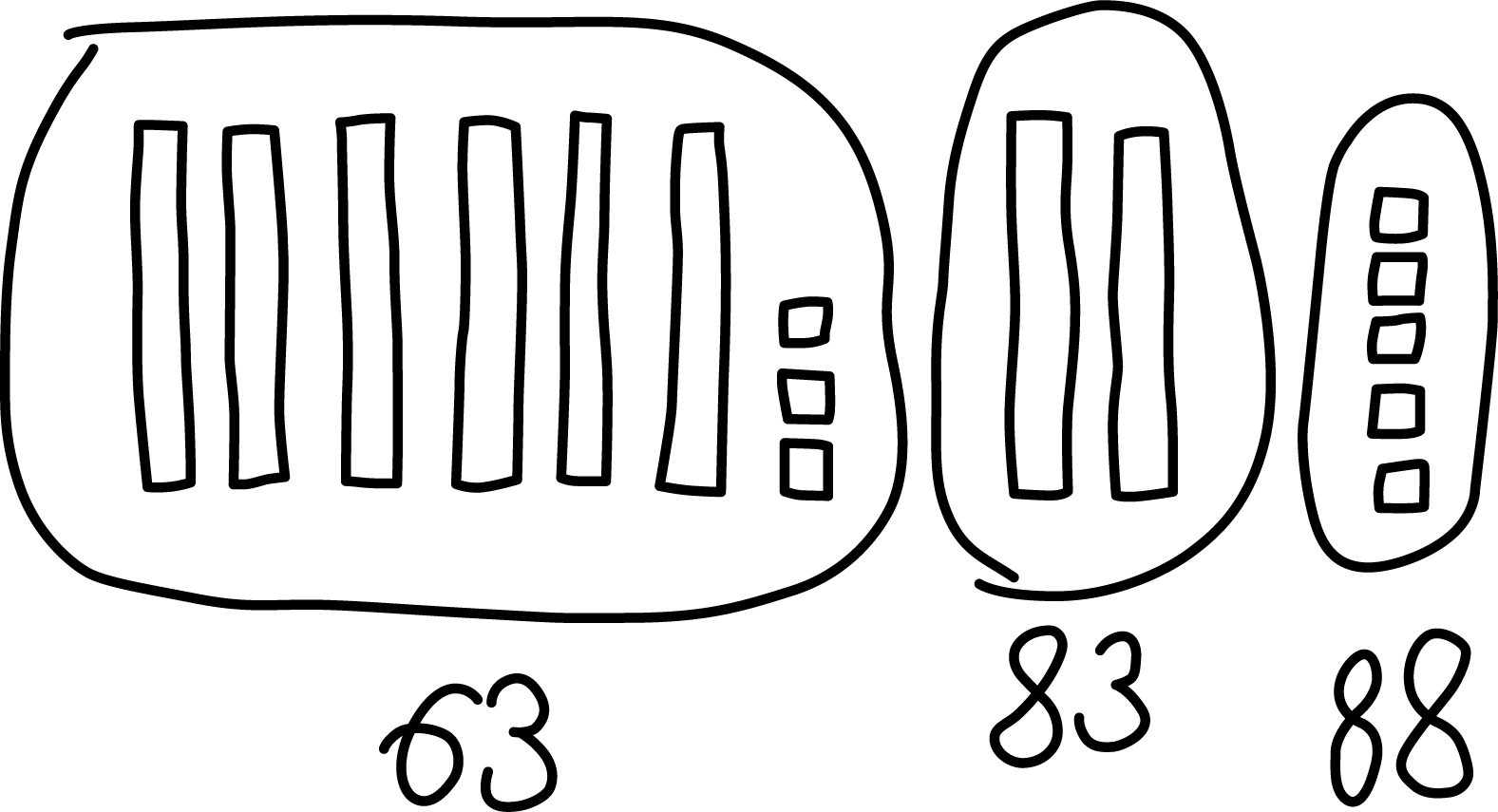
Which equations go with which drawing?
Be ready to explain your thinking in a way others will understand.Set A
\(63+ 20 = 83\)
\(83 + 5 = 88\)Set B
\(60 + 20 = 80\)
\(3 + 5 = 8\)
\(80 + 8 = 88\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Display Elena’s work and the matching equations.
- “How do these equations match the drawing?” (You can see she added the 60 and the 20 and then added the 3 and the 5.)
- “How would you describe how Elena found the sum?” (She added tens and tens, then ones and ones. Then she added the total number of tens and ones together.)
- Display Andre's work and the matching equations.
- “How do these equations match the drawing?” (He started with the 63 then added 20 then added the 5.)
- “How would you describe how Andre found the sum?” (He started with 63 and added the tens then he added the ones.)
Activity 3: Introduce Five in a Row, Add Within 100 without Composing (15 minutes)
Narrative
The purpose of this activity is for students to learn stage 5 of the Five in a Row center. Students add within 100, without composing a ten. Partner A chooses two numbers and places a paperclip on each number. They add the numbers and place a counter on the sum. Partner B moves one of the paperclips to a different number, adds the numbers, and places a counter on the sum. Students take turns moving one paper clip, finding the sum and covering it with a counter. The winner is the first one to get five counters in a row. Two gameboards are provided, one where students add a one-digit and a two-digit number and one where they add a two-digit and a two-digit number. For this activity, students work with the gameboard with one-digit numbers.
Required Materials
Materials to Gather
Materials to Copy
- Five in a Row Addition and Subtraction Stage 5 Gameboard
Launch
- Groups of 2
- Give each group two paper clips, a gameboard, and two-color counters.
- “We are going to learn a new way to play Five in a Row.”
- Display the gameboard.
- “The first player chooses one number from each row to add together. They place a paper clip on each number.”
- Demonstrate putting a paper clip on a one-digit number and on a two-digit number.
- “Then that player finds the sum of the numbers and puts a counter on the sum on the gameboard.”
- Demonstrate finding the sum of the two numbers and placing the counter on the gameboard.
- “The next player only moves one of the paper clips to a new number. Then they find the sum of their two numbers and cover it with a counter on the gameboard. Continue taking turns moving one paper clip and covering numbers on the gameboard until someone gets five counters in a row. They are the winner.”
Activity
- 8 minutes: partner work time
Activity Synthesis
- “How did you decide which paper clip to move?”(I looked at the gameboard and saw which numbers I needed to cover. I tried to find numbers that would have that sum.)
Lesson Synthesis
Lesson Synthesis
“Today we saw that there are different methods that can be used to add 2 two-digit numbers. What method did you see today that you would like to try tomorrow?” (I want to try adding the tens and tens then the ones and ones. I want to try starting with one number and adding on the tens and then the ones.)
Cool-down: Unit 5, Section A Checkpoint (0 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.