Lesson 10
Tens and Tens, Ones and Ones
Warm-up: How Many Do You See: Tens and Ones (10 minutes)
Narrative
The purpose of this How Many Do You See is for students to subitize or use grouping strategies to describe the images they see. Students may put the tens together and the ones together, which is a method for adding that will be used later in this lesson. Students may also use the 10-frames to make a new ten in order to find the total number of counters.
Launch
- Groups of 2
- “How many do you see? How do you see them?”
- Flash image.
- 30 seconds: quiet think time
Activity
- Display image.
- “Discuss your thinking with your partner.”
- 1 minute: partner discussion
- Record responses.
- Repeat for each image.
Student Facing
How many do you see?
How do you see them?



Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “Did anyone see the counters the same way but would explain it differently?”
Activity 1: Priya‘s Work (10 minutes)
Narrative
The purpose of this activity is for students to analyze a base-ten drawing used to find the value of \(37 + 26\), in which a student adds tens and tens and ones and ones. Students make sense of the method used, and consider what made the representation of this method easy for them to understand. This will be helpful when students are asked to represent their addition methods in a way that makes sense to others.
This activity uses MLR8 Discussion Supports. Advances: listening, speaking, conversing
Supports accessibility for: Visual-Spatial Processing, Conceptual Processing
Required Materials
Materials to Gather
Launch
- Groups of 2
- Give students access to connecting cubes in towers of 10 and singles.
Activity
- Read the task statement.
- 2 minutes: independent work time
- “Share your thinking with your partner and work together to write an explanation of what Priya did.”
- 5 minutes: partner discussion
Student Facing
Find the value of \(37 + 26\).
Priya's work
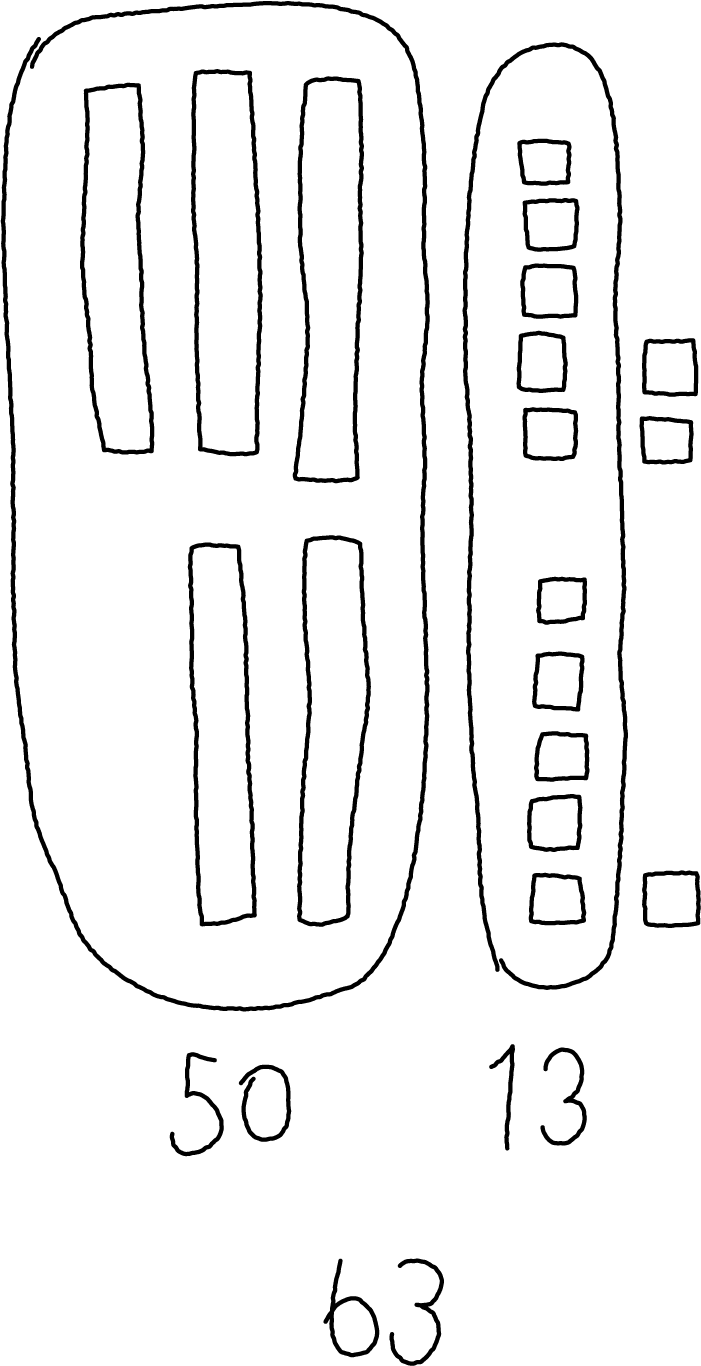
How did Priya find the value?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Invite students to share how they interpreted Priya’s work.
- “Representing our methods in a way that makes sense to others is very important. How did Priya make sure her representation would make sense to others?” (She showed each number clearly. She circled the tens to show she was adding them together. She circled 10 ones to show she made a new ten. She labeled the new ten and the extra ones.)
Activity 2: Finish the Work (15 minutes)
Narrative
The purpose of this activity is for students to consider the associative and commutative properties when adding 2 two-digit numbers. In the first two problems, a base-ten drawing and an expression representing adding tens and tens or ones and ones is given as the first step. Students determine the next steps and find the sum. When students decompose the 2 two-digit numbers into tens and ones, combine the tens and ones, and then find the total, they use their place value understanding to make sense of addition (MP7).
During the activity synthesis, the teacher records students’ thinking using premade posters of 34 and 57 as tens and ones. Students discuss that you can add the parts of the numbers in any order.
Advances: Conversing, Speaking, Listening
Required Materials
Materials to Gather
Required Preparation
- Create two separate posters that show base-ten drawings of 34 and 57. Leave space to write equations underneath the drawings.
Launch
- Groups of 2
- Give students access to connecting cubes in towers of 10 and singles.
- Read the first problem.
- 4 minutes: partner work time
- “What is the difference between how you solved \(28 + 56\) and \(27 + 44\).” (For \(28 + 56\), I added the tens first, then the ones. For \(27 + 44\) I added the ones first, then the tens.)
- 1 minute: partner discussion
- Share responses.
Activity
- Read the next problem.
- 4 minutes: independent work time
- 2 minutes: partner discussion
- Monitor for a student who starts by adding the tens and a student who starts by adding the ones for \(34 + 57\).
Student Facing
-
Each expression shows a first step to find the number that makes each equation true.
Finish the work to find the number that makes each equation true.
Show your thinking using drawings, numbers, or words.-
\(28 + 56=\boxed{\phantom{\frac{aaai}{aaai}}}\)
First step: \(20 + 50\)

-
\(27 + 44=\boxed{\phantom{\frac{aaai}{aaai}}}\)
First step: \(7 + 4\)
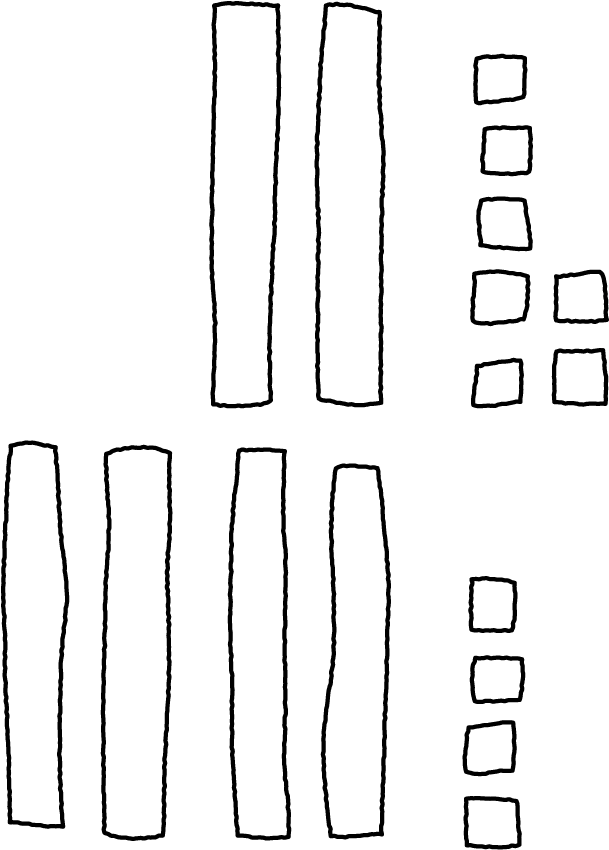
-
-
Find the value of each sum.
Show your thinking using drawings, numbers, or words.- \(34 + 57\)
- \(18 + 55\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Invite previously identified students to share.
- Use the prepared posters to represent each student’s thinking.
- “How are these methods the same? How are they different?” (They both add tens and tens and ones and ones. One person added ones first and the other added tens first. They got the same answer whether they added tens first or ones first.)
- “Why do they both work?” (You can add in any order and you still get the same number.)
Activity 3: Introduce Number Puzzles, Within 100 with Composing (15 minutes)
Narrative
Required Materials
Materials to Gather
Materials to Copy
- Number Puzzles Addition Stage 4 Gameboard
Required Preparation
- Each group of 2 needs a set of digit cards from the previous center, Number Puzzles.
Launch
- Groups of 2
- Give each group a set of cards and gameboards.
- “These number puzzles have addition equations with two-digit numbers. Use the digit cards to make each equation true. Remember that you can only use each card once on a page.”
Activity
- 10 minutes: partner work time
Activity Synthesis
- Display a gameboard.
- “Which equation can you fill in first?”
Lesson Synthesis
Lesson Synthesis
Display posters from the Activity 2 synthesis.
“Today we added tens and tens and ones and ones and saw that we can add the ones first or the tens first. Do you prefer to add the ones first or the tens first? Why do you like that method better?” (I like to add the tens first because they come first in the number. I like to add the ones first because I like to add numbers that make a new ten.)
Cool-down: Unit 5, Section C Checkpoint (0 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.